
Question and Answers Forum
Question Number 63711 by mathmax by abdo last updated on 07/Jul/19
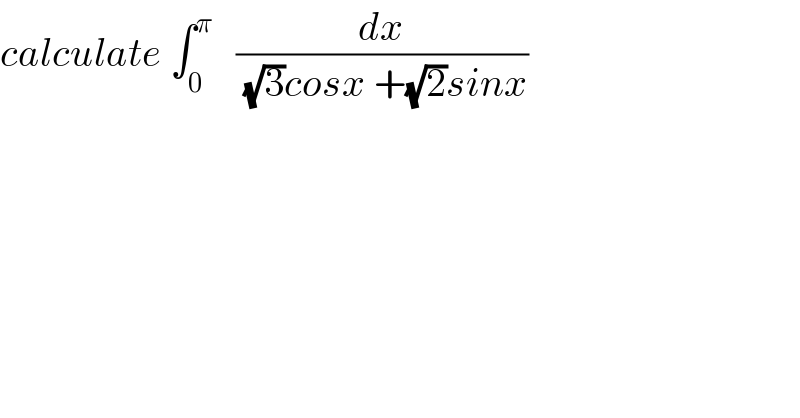
Commented by mathmax by abdo last updated on 08/Jul/19
![let A =∫_0 ^π (dx/((√3)cosx +(√2)sinx)) changement tan((x/2))=t give A =∫_0 ^∞ ((2dt)/((1+t^2 ){(√3)((1−t^2 )/(1+t^2 )) +(√2)((2t)/(1+t^2 ))})) =∫_0 ^∞ ((2dt)/((√3)(1−t^2 )+2(√2)t)) =∫_0 ^∞ ((2dt)/(−(√3)t^2 +2(√2)t +(√3))) =∫_0 ^∞ ((−2dt)/((√3)t^2 −2(√2)t−(√3))) Δ^′ =(−(√2))^2 +3 =5 ⇒t_1 =(((√2)+(√5))/(√3)) and t_2 =(((√2)−(√5))/(√3)) ⇒ A =((−2)/(√3))∫_0 ^∞ (dt/((t−t_1 )(t−t_2 ))) =((−2)/((√3)(t_1 −t_2 ))) ∫_0 ^∞ {(1/(t−t_1 )) −(1/(t−t_2 ))}dt =((−2)/((√3)((2(√5))/(√3)))) ∫_0 ^∞ {(1/(t−t_1 )) −(1/(t−t_2 ))}dt=−(1/(√5))[ln∣((t−t_1 )/(t−t_2 ))∣]_0 ^(+∞) =(1/(√5))ln∣(t_1 /t_2 )∣ =(1/(√5))ln∣(((√2)+(√5))/((√2)−(√5)))∣ =(1/(√5))ln((((√5)+(√2))/((√5)−(√2)))).](Q63767.png)
Answered by MJS last updated on 07/Jul/19
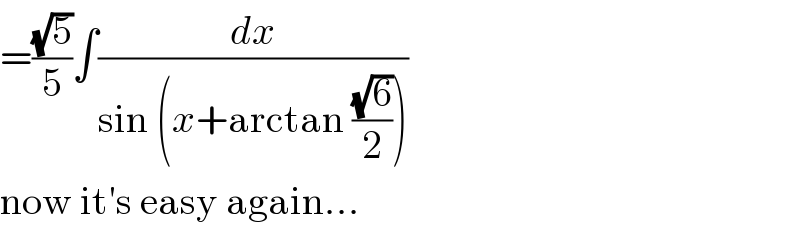
Commented by mathmax by abdo last updated on 07/Jul/19

| ||
Question and Answers Forum | ||
Question Number 63711 by mathmax by abdo last updated on 07/Jul/19 | ||
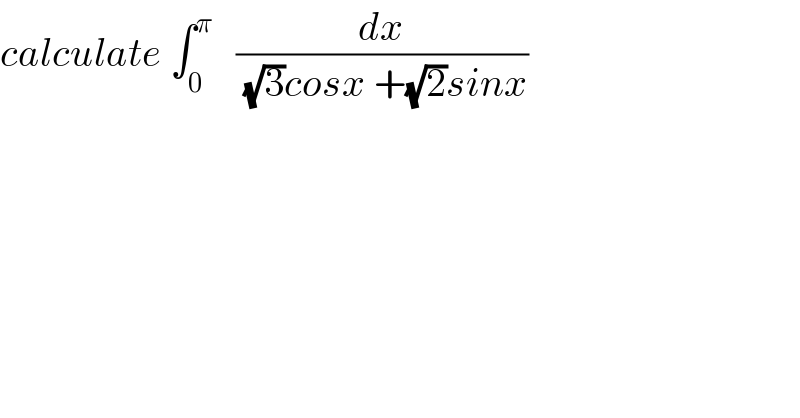 | ||
Commented by mathmax by abdo last updated on 08/Jul/19 | ||
![let A =∫_0 ^π (dx/((√3)cosx +(√2)sinx)) changement tan((x/2))=t give A =∫_0 ^∞ ((2dt)/((1+t^2 ){(√3)((1−t^2 )/(1+t^2 )) +(√2)((2t)/(1+t^2 ))})) =∫_0 ^∞ ((2dt)/((√3)(1−t^2 )+2(√2)t)) =∫_0 ^∞ ((2dt)/(−(√3)t^2 +2(√2)t +(√3))) =∫_0 ^∞ ((−2dt)/((√3)t^2 −2(√2)t−(√3))) Δ^′ =(−(√2))^2 +3 =5 ⇒t_1 =(((√2)+(√5))/(√3)) and t_2 =(((√2)−(√5))/(√3)) ⇒ A =((−2)/(√3))∫_0 ^∞ (dt/((t−t_1 )(t−t_2 ))) =((−2)/((√3)(t_1 −t_2 ))) ∫_0 ^∞ {(1/(t−t_1 )) −(1/(t−t_2 ))}dt =((−2)/((√3)((2(√5))/(√3)))) ∫_0 ^∞ {(1/(t−t_1 )) −(1/(t−t_2 ))}dt=−(1/(√5))[ln∣((t−t_1 )/(t−t_2 ))∣]_0 ^(+∞) =(1/(√5))ln∣(t_1 /t_2 )∣ =(1/(√5))ln∣(((√2)+(√5))/((√2)−(√5)))∣ =(1/(√5))ln((((√5)+(√2))/((√5)−(√2)))).](Q63767.png) | ||
Answered by MJS last updated on 07/Jul/19 | ||
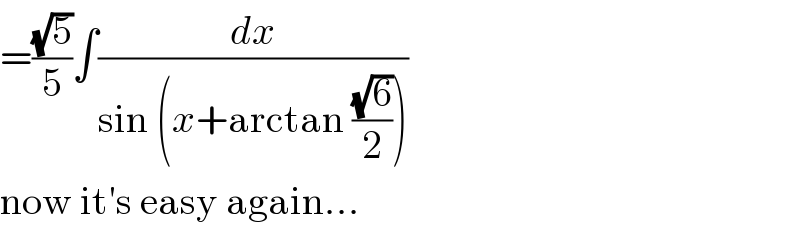 | ||
| ||
Commented by mathmax by abdo last updated on 07/Jul/19 | ||
 | ||