
Question and Answers Forum
Question Number 63784 by MJS last updated on 09/Jul/19

Commented by Prithwish sen last updated on 09/Jul/19
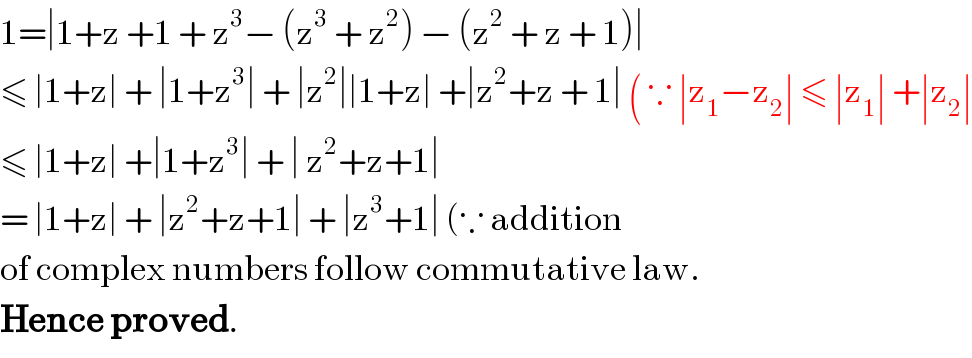
Commented by Prithwish sen last updated on 09/Jul/19

Commented by Prithwish sen last updated on 09/Jul/19

Commented by mr W last updated on 09/Jul/19
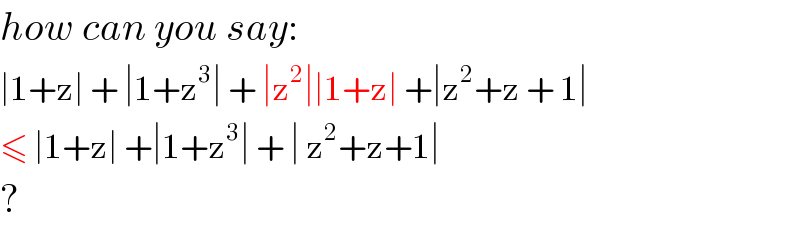
Commented by MJS last updated on 10/Jul/19
![so how can we solve it? for z=−1 0+1+0≥1 for z=−(1/2)±((√3)/2)i 1+0+2≥1 for z=(1/2)±((√3)/2)i (√3)+2+0≥1 is it enough to show that for z close to −1 the sum of the absolutes is rising in every direction? we can put x=−1+re^(iθ) with −π≤θ<π and choose any small value for r>0 ⇒ ∣z+1∣+∣z^2 +z+1∣+∣z^3 +1∣=f(θ)= =r+(√(r^4 −2r^3 cos θ −(1−4cos^2 θ)r^2 −2rcos θ +1))+r(√(r^4 −6r^3 cos θ +3(1+4cos^2 θ)r^2 −18rcos θ +9)) (df/dθ)=rsin θ ×[some complicated term which has no zeros for small values of r] ⇒ our function has minima/maxima at θ=−π∨θ=0 ⇒ { ((f(−π)=r+∣r^2 +r+1∣+r∣r^2 +3r+3∣)),((f(0)=r+∣r^2 −r+1∣+r∣r^2 −3r+3∣)) :} in both cases the minimum is at r=0 because r cannot be negative ⇒ z=−1 seems to be the absolute minimum with ∣z+1∣+∣z^2 +z+1∣+∣z^3 +1∣=1](Q63826.png)
Commented by Prithwish sen last updated on 10/Jul/19

