Question and Answers Forum
Question Number 63803 by aliesam last updated on 09/Jul/19

Commented by Prithwish sen last updated on 09/Jul/19
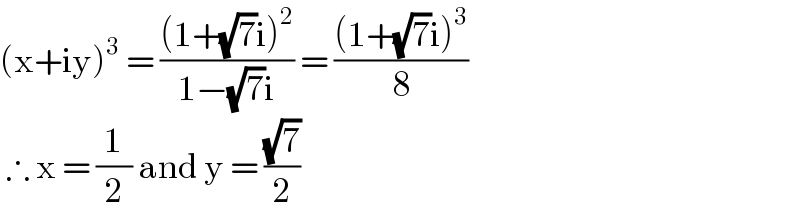
Commented by mathmax by abdo last updated on 09/Jul/19
![let Z =x+iy we get Z^3 =((−6+2(√7)i)/(1−(√7)i)) let solve this (e) ∣−6+2(√7)i∣ =(√(36+28))=(√(64))=8 ∣1−(√7)i∣ =(√(1+7))=(√8) ⇒∣((−6+2(√(i7)))/(1−(√7)i))∣ =(8/(√8)) =2(√2) −6+2(√7)i =8(((−6)/8) +((2(√7)i)/8)) =8(−(3/4) +((√7)/4)i) =8 e^(iarctan(−((√7)/3))) 1−(√7)i =2(√2)( (1/(2(√2))) −((√7)/(2(√2)))i) =2(√2) e^(iarctan(−(√7))) ⇒ ((−6+2(√7)i)/(1−(√7)i)) =2(√2)e^(i( arctan(((−(√7))/3))+arctan((√7)))) =2(√2) e^(i(arctan((√7))−arctan(((√7)/3)))) let Z =ρ e^(iθ) (e) ⇒ρ^3 e^(i3θ) =2(√2)e^(i(arctan(√7)−arctan(((√7)/3))) ) ⇒ ρ =(2(√2))^(1/3) and 3θ =arctan((√7))−arctan(((√7)/3)) +2kπ ⇒ ⇒θ_k =((arctan((√7))−arctan(((√7)/3)))/3) +((2kπ)/3) and k ∈[[0,2]] the roots are Z_k =e^(iθ_k ) =x_k +iy_k Z_0 =e^(iθ_0 ) =x_0 +iy_0 Z_1 =e^(iθ_1 ) =x_1 +iy_1 Z_2 =e^(iθ_2 ) =x_2 +iy_2 ...](Q63805.png)
Commented by mathmax by abdo last updated on 09/Jul/19
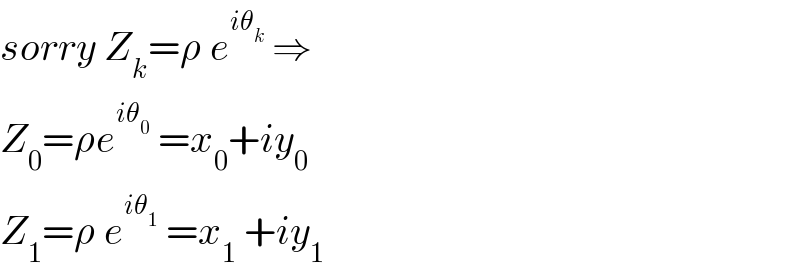
Commented by mathmax by abdo last updated on 09/Jul/19
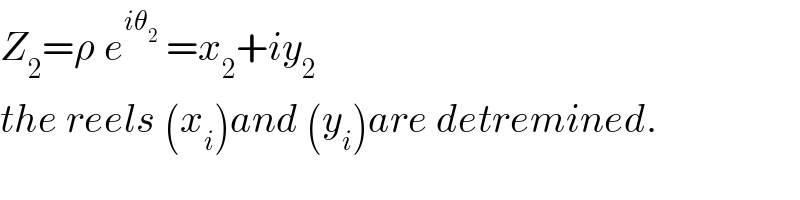
Answered by MJS last updated on 09/Jul/19