
Question and Answers Forum
Question Number 63893 by mathmax by abdo last updated on 10/Jul/19
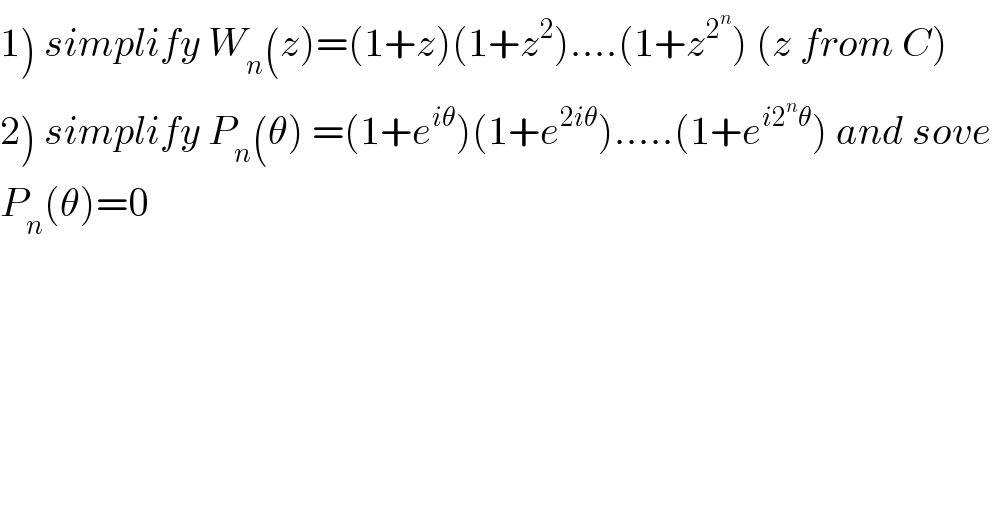
Commented by mathmax by abdo last updated on 05/Nov/19
![1) we have W_n (z)=(1+z)(1+z^2 )....(1+z^2^n ) let prove by recurrence that W_n (z)=((1−z^2^(n+1) )/(1−z)) n =0 →W_n (z)=1+z =((1−z^2 )/(1−z))(true) let suppose the relation true W_(n+1) =(1+z)(1+z^2 )....(1+z^2^(n+1) )=(1+z)(1+z^2 )...(1+z^2^n )(1+z^2^(n+1) ) =((1−z^2^(n+1) )/(1−z))×(1+z^2^(n+1) )=((1+z^2^(n+1) −z^2^(n+1) −z^2^(n+2) )/(1−z)) =((1−z^2^(n+2) )/(1−z)) c/c W_n (z)=((1−z^2^(n+1) )/(1−z)) with z≠1 2) P_n (θ)=(1+e^(iθ) )(1+e^(2iθ) ).....(1+e^(i 2^n θ) ) =(1+e^(iθ) )(1+(e^(iθ) )^2 ).....(1+(e^(iθ) )^2^n )=W_n (e^(iθ) ) =((1−(e^(iθ) )^2^(n+1) )/(1−e^(iθ) )) =((1−e^(i2^(n+1) θ) )/(1−e^(iθ) )) (if θ ≠2kπ) P_n (θ)=0 ⇔1−e^(i2^(n+1) θ) =0 ⇒e^(i2^(n+1) θ) =e^(i2kπ) ⇒ θ_k =((2kπ)/2^(n+1) ) =((kπ)/2^n ) with k∈[[1,2^(n+1) −1]]](Q72991.png)
| ||
Question and Answers Forum | ||
Question Number 63893 by mathmax by abdo last updated on 10/Jul/19 | ||
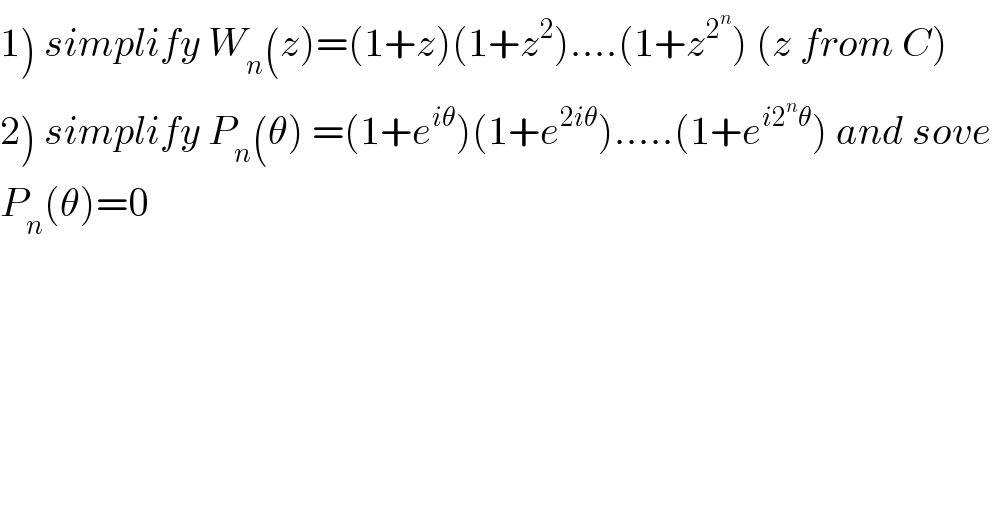 | ||
Commented by mathmax by abdo last updated on 05/Nov/19 | ||
![1) we have W_n (z)=(1+z)(1+z^2 )....(1+z^2^n ) let prove by recurrence that W_n (z)=((1−z^2^(n+1) )/(1−z)) n =0 →W_n (z)=1+z =((1−z^2 )/(1−z))(true) let suppose the relation true W_(n+1) =(1+z)(1+z^2 )....(1+z^2^(n+1) )=(1+z)(1+z^2 )...(1+z^2^n )(1+z^2^(n+1) ) =((1−z^2^(n+1) )/(1−z))×(1+z^2^(n+1) )=((1+z^2^(n+1) −z^2^(n+1) −z^2^(n+2) )/(1−z)) =((1−z^2^(n+2) )/(1−z)) c/c W_n (z)=((1−z^2^(n+1) )/(1−z)) with z≠1 2) P_n (θ)=(1+e^(iθ) )(1+e^(2iθ) ).....(1+e^(i 2^n θ) ) =(1+e^(iθ) )(1+(e^(iθ) )^2 ).....(1+(e^(iθ) )^2^n )=W_n (e^(iθ) ) =((1−(e^(iθ) )^2^(n+1) )/(1−e^(iθ) )) =((1−e^(i2^(n+1) θ) )/(1−e^(iθ) )) (if θ ≠2kπ) P_n (θ)=0 ⇔1−e^(i2^(n+1) θ) =0 ⇒e^(i2^(n+1) θ) =e^(i2kπ) ⇒ θ_k =((2kπ)/2^(n+1) ) =((kπ)/2^n ) with k∈[[1,2^(n+1) −1]]](Q72991.png) | ||