Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 63919 by raj last updated on 11/Jul/19

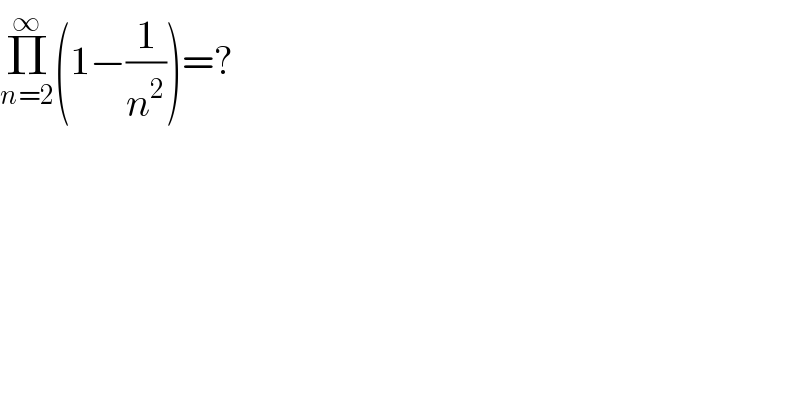
Π_(n=2) ^∞ (1−(1/n^2 ))=?

$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)=? \\ $$

Commented by Prithwish sen last updated on 11/Jul/19

Π_(n=2) ^(n=n) (1−(1/n^2 )) = ((1.2.3^2 .4^2 ...........n.(n+1))/(1^2 .2^2 .3^2 ..........(n−1)^2 .n^2 )) = [(((n+1)!)/(n!))]^2 .(1/(2n(n+1))) = (((n+1)^2 )/(2n(n+1))) = (1/2)(1+(1/n)) → (1/2) as n→∞ please check.

$$\underset{\mathrm{n}=\mathrm{2}} {\overset{\mathrm{n}=\boldsymbol{\mathrm{n}}} {\prod}}\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\:=\:\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}^{\mathrm{2}} .\mathrm{4}^{\mathrm{2}} ...........\mathrm{n}.\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{1}^{\mathrm{2}} .\mathrm{2}^{\mathrm{2}} .\mathrm{3}^{\mathrm{2}} ..........\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{2}} .\mathrm{n}^{\mathrm{2}} }\: \\ $$$$=\:\left[\frac{\left(\mathrm{n}+\mathrm{1}\right)!}{\mathrm{n}!}\right]^{\mathrm{2}} .\frac{\mathrm{1}}{\mathrm{2n}\left(\mathrm{n}+\mathrm{1}\right)}\:=\:\frac{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2n}\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)\:\rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{as}\:\mathrm{n}\rightarrow\infty \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$

Commented by mathmax by abdo last updated on 11/Jul/19

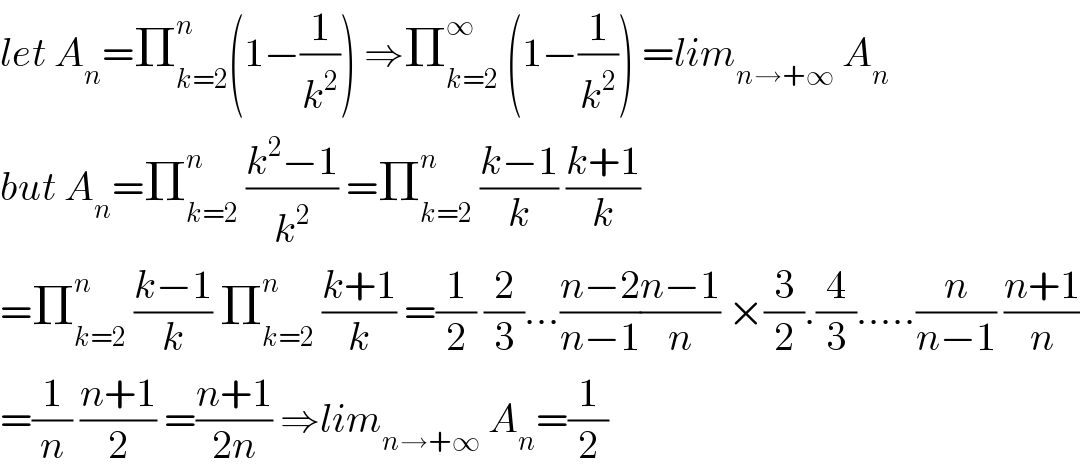
let A_n =Π_(k=2) ^n (1−(1/k^2 )) ⇒Π_(k=2) ^∞ (1−(1/k^2 )) =lim_(n→+∞) A_n but A_n =Π_(k=2) ^n ((k^2 −1)/k^2 ) =Π_(k=2) ^n ((k−1)/k) ((k+1)/k) =Π_(k=2) ^n ((k−1)/k) Π_(k=2) ^n ((k+1)/k) =(1/2) (2/3)...((n−2)/(n−1))((n−1)/n) ×(3/2).(4/3).....(n/(n−1)) ((n+1)/n) =(1/n) ((n+1)/2) =((n+1)/(2n)) ⇒lim_(n→+∞) A_n =(1/2)

$${let}\:{A}_{{n}} =\prod_{{k}=\mathrm{2}} ^{{n}} \left(\mathrm{1}−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right)\:\Rightarrow\prod_{{k}=\mathrm{2}} ^{\infty} \:\left(\mathrm{1}−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right)\:={lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \\ $$$${but}\:{A}_{{n}} =\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{{k}^{\mathrm{2}} −\mathrm{1}}{{k}^{\mathrm{2}} }\:=\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{{k}−\mathrm{1}}{{k}}\:\frac{{k}+\mathrm{1}}{{k}} \\ $$$$=\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{{k}−\mathrm{1}}{{k}}\:\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{{k}+\mathrm{1}}{{k}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{2}}{\mathrm{3}}...\frac{{n}−\mathrm{2}}{{n}−\mathrm{1}}\frac{{n}−\mathrm{1}}{{n}}\:×\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{4}}{\mathrm{3}}.....\frac{{n}}{{n}−\mathrm{1}}\:\frac{{n}+\mathrm{1}}{{n}} \\ $$$$=\frac{\mathrm{1}}{{n}}\:\frac{{n}+\mathrm{1}}{\mathrm{2}}\:=\frac{{n}+\mathrm{1}}{\mathrm{2}{n}}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by raj last updated on 11/Jul/19

thank you

$${thank}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com