Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 63920 by raj last updated on 11/Jul/19

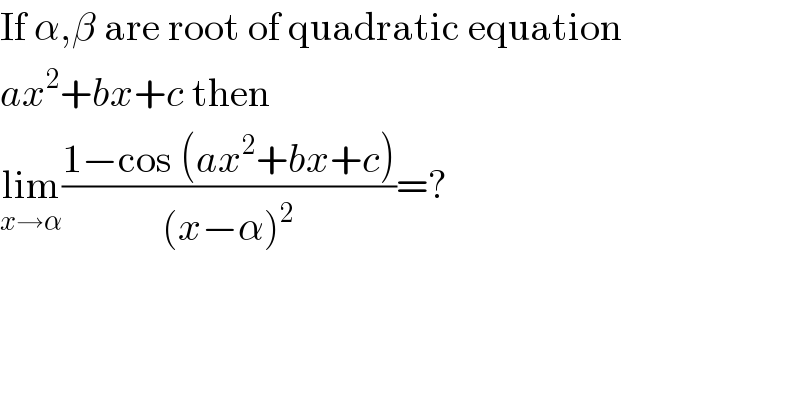
If α,β are root of quadratic equation ax^2 +bx+c then lim_(x→α) ((1−cos (ax^2 +bx+c))/((x−α)^2 ))=?

$$\mathrm{If}\:\alpha,\beta\:\mathrm{are}\:\mathrm{root}\:\mathrm{of}\:\mathrm{quadratic}\:\mathrm{equation} \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}\:\mathrm{then} \\ $$$$\underset{{x}\rightarrow\alpha} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\left({ax}^{\mathrm{2}} +{bx}+{c}\right)}{\left({x}−\alpha\right)^{\mathrm{2}} }=? \\ $$

Commented by Prithwish sen last updated on 11/Jul/19

=Lt[((sin(((x−α)(x−β))/2))/(((x−α)(x−β))/2))]^2 .(((x−β)^2 )/2) =(((α−β)^2 )/2) please check.

$$=\mathrm{Lt}\left[\frac{\mathrm{sin}\frac{\left(\mathrm{x}−\alpha\right)\left(\mathrm{x}−\beta\right)}{\mathrm{2}}}{\frac{\left(\mathrm{x}−\alpha\right)\left(\mathrm{x}−\beta\right)}{\mathrm{2}}}\right]^{\mathrm{2}} .\frac{\left(\mathrm{x}−\beta\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\frac{\left(\alpha−\beta\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$

Commented by kaivan.ahmadi last updated on 11/Jul/19

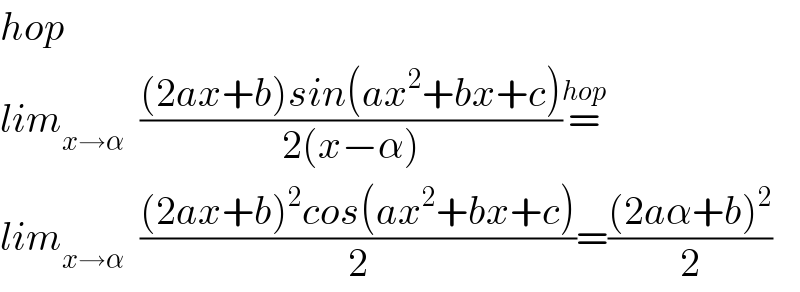
hop lim_(x→α) (((2ax+b)sin(ax^2 +bx+c))/(2(x−α)))=^(hop) lim_(x→α) (((2ax+b)^2 cos(ax^2 +bx+c))/2)=(((2aα+b)^2 )/2)

$${hop} \\ $$$${lim}_{{x}\rightarrow\alpha} \:\:\frac{\left(\mathrm{2}{ax}+{b}\right){sin}\left({ax}^{\mathrm{2}} +{bx}+{c}\right)}{\mathrm{2}\left({x}−\alpha\right)}\overset{{hop}} {=} \\ $$$${lim}_{{x}\rightarrow\alpha} \:\:\frac{\left(\mathrm{2}{ax}+{b}\right)^{\mathrm{2}} {cos}\left({ax}^{\mathrm{2}} +{bx}+{c}\right)}{\mathrm{2}}=\frac{\left(\mathrm{2}{a}\alpha+{b}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$

Commented by mathmax by abdo last updated on 11/Jul/19

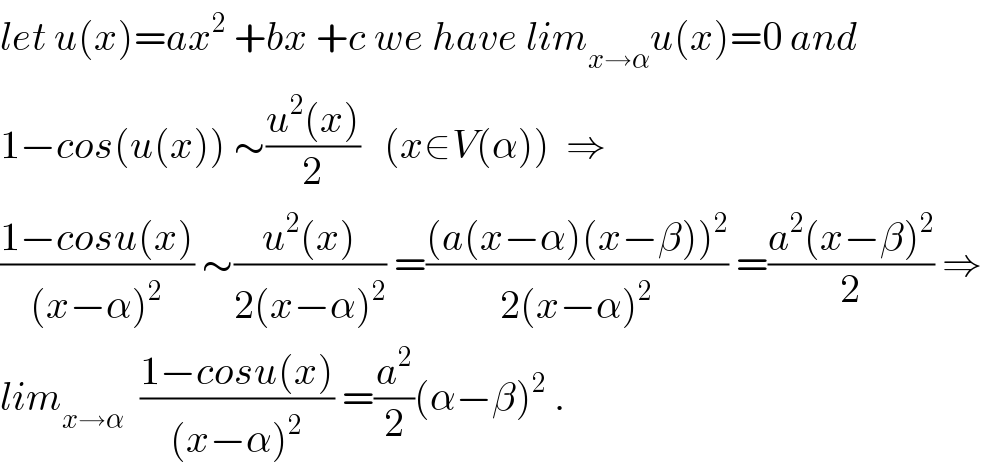
let u(x)=ax^2 +bx +c we have lim_(x→α) u(x)=0 and 1−cos(u(x)) ∼((u^2 (x))/2) (x∈V(α)) ⇒ ((1−cosu(x))/((x−α)^2 )) ∼((u^2 (x))/(2(x−α)^2 )) =(((a(x−α)(x−β))^2 )/(2(x−α)^2 )) =((a^2 (x−β)^2 )/2) ⇒ lim_(x→α) ((1−cosu(x))/((x−α)^2 )) =(a^2 /2)(α−β)^2 .

$${let}\:{u}\left({x}\right)={ax}^{\mathrm{2}} \:+{bx}\:+{c}\:{we}\:{have}\:{lim}_{{x}\rightarrow\alpha} {u}\left({x}\right)=\mathrm{0}\:{and}\: \\ $$$$\mathrm{1}−{cos}\left({u}\left({x}\right)\right)\:\sim\frac{{u}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}}\:\:\:\left({x}\in{V}\left(\alpha\right)\right)\:\:\Rightarrow \\ $$$$\frac{\mathrm{1}−{cosu}\left({x}\right)}{\left({x}−\alpha\right)^{\mathrm{2}} }\:\sim\frac{{u}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}\left({x}−\alpha\right)^{\mathrm{2}} }\:=\frac{\left({a}\left({x}−\alpha\right)\left({x}−\beta\right)\right)^{\mathrm{2}} }{\mathrm{2}\left({x}−\alpha\right)^{\mathrm{2}} }\:=\frac{{a}^{\mathrm{2}} \left({x}−\beta\right)^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\alpha} \:\:\frac{\mathrm{1}−{cosu}\left({x}\right)}{\left({x}−\alpha\right)^{\mathrm{2}} }\:=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\alpha−\beta\right)^{\mathrm{2}} \:. \\ $$

Commented by raj last updated on 11/Jul/19

thank you

$${thank}\:{you} \\ $$

Commented by mathmax by abdo last updated on 12/Jul/19

you are welcome.

$${you}\:{are}\:{welcome}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com