Question and Answers Forum
Question Number 64009 by ajfour last updated on 12/Jul/19
Commented by ajfour last updated on 12/Jul/19
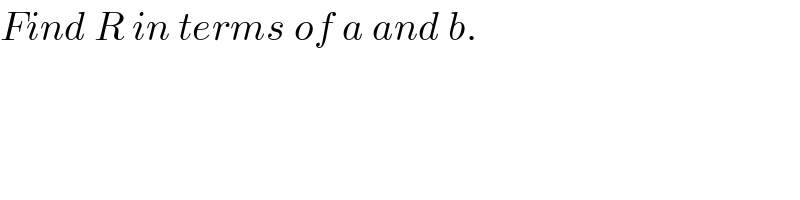
Answered by mr W last updated on 12/Jul/19
Commented by mr W last updated on 12/Jul/19
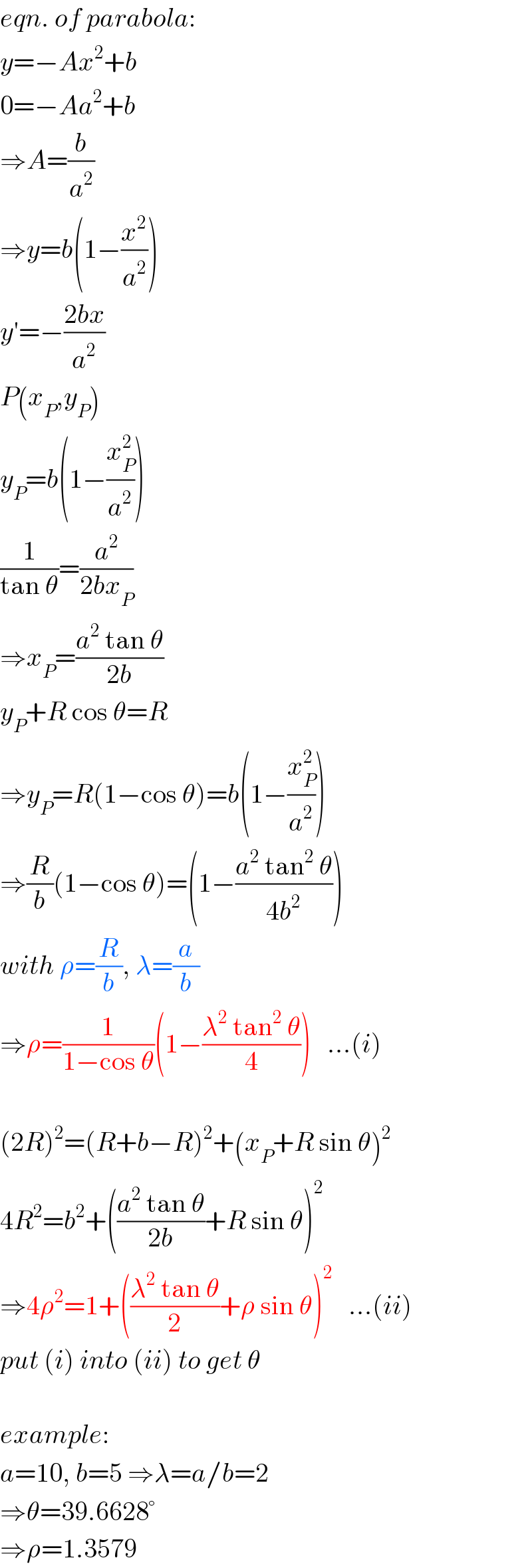
Commented by mr W last updated on 12/Jul/19
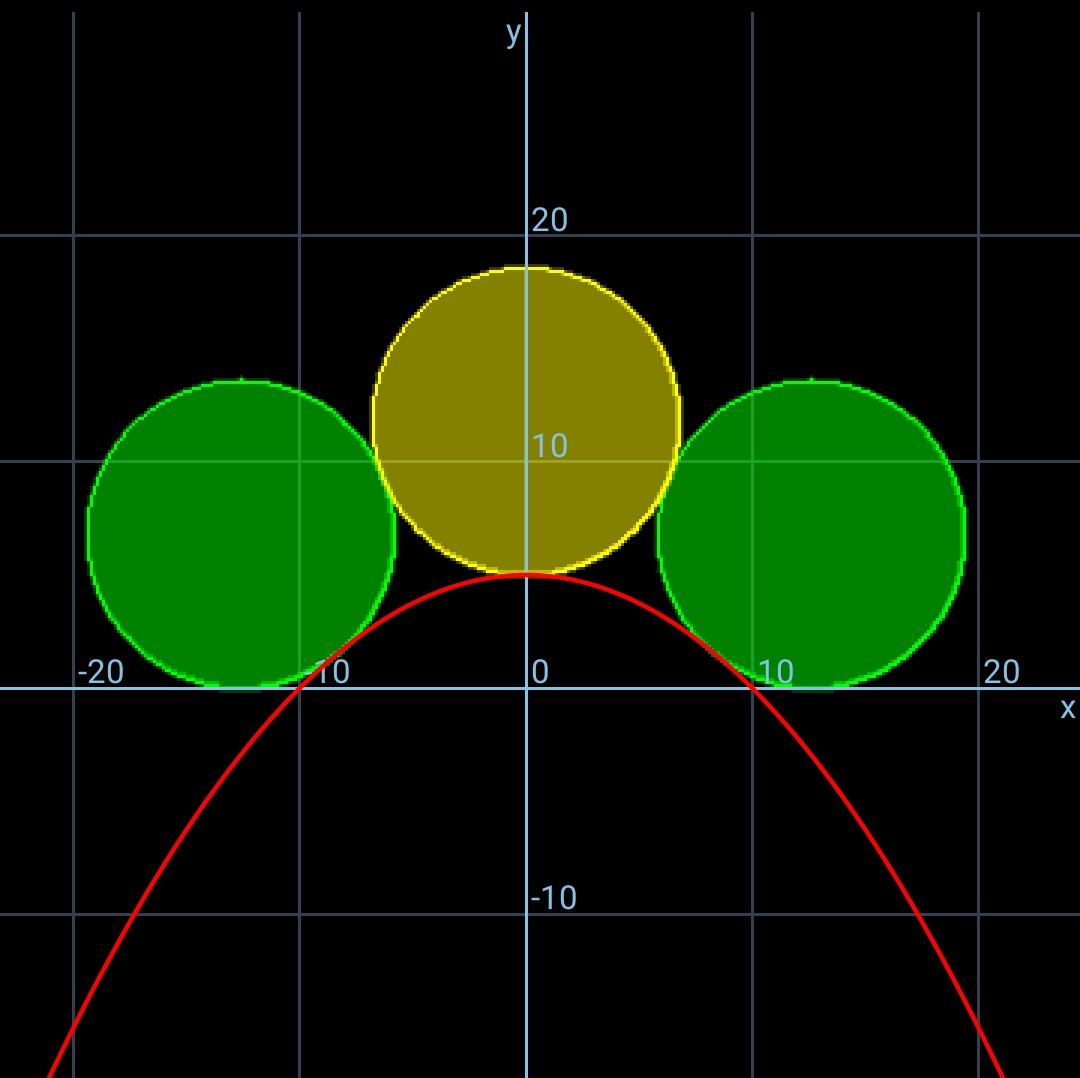
Commented by ajfour last updated on 12/Jul/19
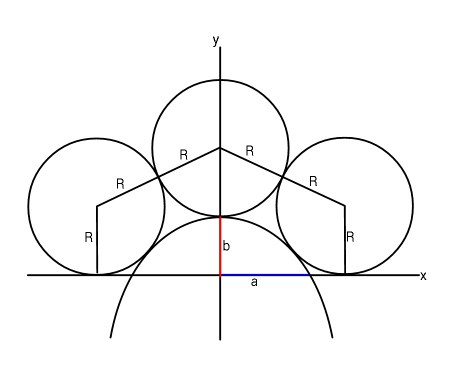
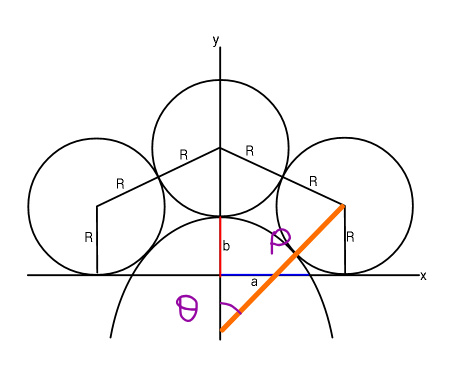
Answered by ajfour last updated on 12/Jul/19
![y=Ax^2 +b 0=Aa^2 +b ⇒ A=−b/a^2 let parabola touch the circle on right at (h,k). k=b(1−(h^2 /a^2 )) (dy/dx)=2Ax = 2(−(b/a^2 ))h slope of normal tan θ=(a^2 /(2bh)) let centre of right circle be C(p,q) p=h+Rcos θ , q=k+Rsin θ Now q=R and p^2 +b^2 =4R^2 ⇒ R=b(1−(h^2 /a^2 ))+Rsin θ (h+Rcos θ)^2 +b^2 =4R^2 tan θ=(a^2 /(2bh)) ⇒ h=((a^2 cos θ)/(2bsin θ)) ⇒ R=b(1−((a^2 cos^2 θ)/(4b^2 sin^2 θ)))+Rsin θ ⇒ R=(b/((1−sin θ)))(1−((a^2 cos^2 θ)/(4b^2 sin^2 θ))) (((a^2 cos θ)/(2bsin θ))+Rcos θ)^2 =4R^2 −b^2 [((a^2 cos θ)/(2bsin θ))+((b(1−((a^2 cos^2 θ)/(4b^2 sin^2 θ)))cos θ)/(1−sin θ))]^2 =[((2b(1−((a^2 cos^2 θ)/(4b^2 sin^2 θ))))/(1−sin θ))]^2 −b^2 let sin θ=t ⇒ (1−t^2 )[(a^2 /(2bt))+(b/(1−t))(1−((a^2 (1−t^2 ))/(4b^2 t^2 )))]^2 =[((2b(1−((a^2 (1−t^2 ))/(4b^2 t^2 ))))/(1−t))]^2 −b^2 ⇒ (1−t^2 )[2a^2 b(1−t)t+b{4b^2 t^2 −a^2 +a^2 t^2 }]^2 +16b^6 (1−t)^2 t^4 = 4b^2 [4b^2 t^2 −a^2 +a^2 t^2 ]^2 ⇒ (1−t^2 )[(4b^2 −a^2 )t^2 +2a^2 t−a^2 ]^2 +16b^4 (1−t)^2 t^4 =4[(a^2 +4b^2 )t^2 −a^2 ]^2 And for a=2, b=1 (1−t^2 )(2t−1)^2 =(1−t)^2 t^4 +4(2t^2 −1)^2 ⇒ t=0.7698144 R=(b/((1−sin θ)))(1−((a^2 cos^2 θ)/(4b^2 sin^2 θ))) R=((2t^2 −1)/(t^2 (1−t))) = 1.35787 ■](Q64063.png)
Commented by mr W last updated on 13/Jul/19