Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 6407 by FilupSmith last updated on 26/Jun/16

Can you evaluate: lim_(x→∞) (−1)^x x WolframAlpha writes the answer as =e^(2i to π) ∞

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{evaluate}: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(−\mathrm{1}\right)^{{x}} {x} \\ $$$$ \\ $$$$\mathrm{WolframAlpha}\:\mathrm{writes}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{as} \\ $$$$={e}^{\mathrm{2}{i}\:\:\mathrm{to}\:\:\pi} \infty \\ $$

Commented by FilupSmith last updated on 26/Jun/16

Is there a more formal way to write the answer?

$$\mathrm{Is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{more}\:\mathrm{formal}\:\mathrm{way}\:\mathrm{to}\:\mathrm{write} \\ $$$$\mathrm{the}\:\mathrm{answer}? \\ $$

Commented by FilupSmith last updated on 26/Jun/16

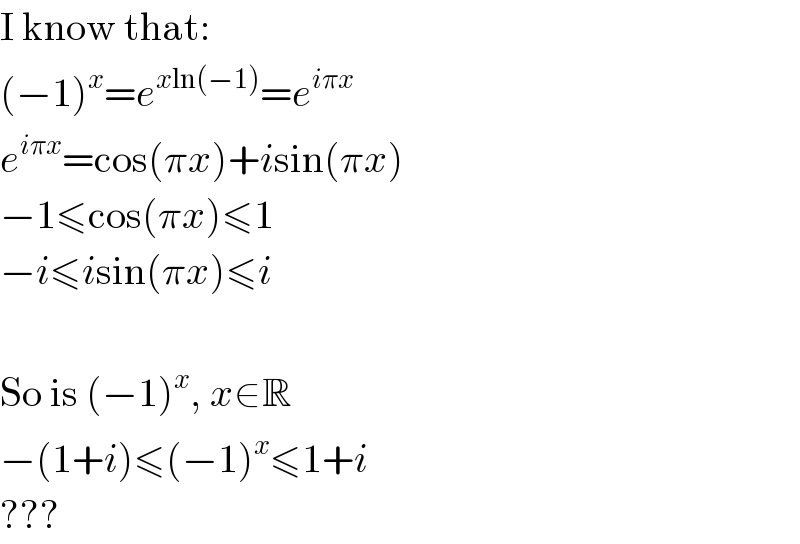
I know that: (−1)^x =e^(xln(−1)) =e^(iπx) e^(iπx) =cos(πx)+isin(πx) −1≤cos(πx)≤1 −i≤isin(πx)≤i So is (−1)^x , x∈R −(1+i)≤(−1)^x ≤1+i ???

$$\mathrm{I}\:\mathrm{know}\:\mathrm{that}: \\ $$$$\left(−\mathrm{1}\right)^{{x}} ={e}^{{x}\mathrm{ln}\left(−\mathrm{1}\right)} ={e}^{{i}\pi{x}} \\ $$$${e}^{{i}\pi{x}} =\mathrm{cos}\left(\pi{x}\right)+{i}\mathrm{sin}\left(\pi{x}\right) \\ $$$$−\mathrm{1}\leqslant\mathrm{cos}\left(\pi{x}\right)\leqslant\mathrm{1} \\ $$$$−{i}\leqslant{i}\mathrm{sin}\left(\pi{x}\right)\leqslant{i} \\ $$$$ \\ $$$$\mathrm{So}\:\mathrm{is}\:\left(−\mathrm{1}\right)^{{x}} ,\:{x}\in\mathbb{R} \\ $$$$−\left(\mathrm{1}+{i}\right)\leqslant\left(−\mathrm{1}\right)^{{x}} \leqslant\mathrm{1}+{i} \\ $$$$??? \\ $$

Answered by Temp last updated on 27/Jun/16

(−1)^x =e^(iπx) e^(iπx) =cos(xπ)+isin(xπ) ℜ(e^(iπx) )=cos(πx) −1≤ℜ(e^(iπx) )≤1 ℑ(e^(iπx) )=sin(πx) −1≤ℑ(e^(iπx) )≤1 Let L=lim_(x→∞) (e^(iπx) ) if L∈R⇒x∈Z:−1≤x≤1 ∴(−1)^x = { ((1 if 2∣x)),((−1 if 2∤x)) :} if L∈C⇒x∈R −(i+1)≤L≤(i+1)

$$\left(−\mathrm{1}\right)^{{x}} ={e}^{{i}\pi{x}} \\ $$$${e}^{{i}\pi{x}} =\mathrm{cos}\left({x}\pi\right)+{i}\mathrm{sin}\left({x}\pi\right) \\ $$$$ \\ $$$$\Re\left({e}^{{i}\pi{x}} \right)=\mathrm{cos}\left(\pi{x}\right) \\ $$$$−\mathrm{1}\leqslant\Re\left({e}^{{i}\pi{x}} \right)\leqslant\mathrm{1} \\ $$$$ \\ $$$$\Im\left({e}^{{i}\pi{x}} \right)=\mathrm{sin}\left(\pi{x}\right) \\ $$$$−\mathrm{1}\leqslant\Im\left({e}^{{i}\pi{x}} \right)\leqslant\mathrm{1} \\ $$$$ \\ $$$$\mathrm{Let}\:{L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({e}^{{i}\pi{x}} \right) \\ $$$$\mathrm{if}\:{L}\in\mathbb{R}\Rightarrow{x}\in\mathbb{Z}:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\therefore\left(−\mathrm{1}\right)^{{x}} =\begin{cases}{\mathrm{1}\:\:\:\mathrm{if}\:\mathrm{2}\mid{x}}\\{−\mathrm{1}\:\:\mathrm{if}\:\mathrm{2}\nmid{x}}\end{cases} \\ $$$$\mathrm{if}\:{L}\in\mathbb{C}\Rightarrow{x}\in\mathbb{R} \\ $$$$−\left({i}+\mathrm{1}\right)\leqslant{L}\leqslant\left({i}+\mathrm{1}\right) \\ $$

Commented by Temp last updated on 27/Jun/16

Im(x)=ℑ(x) Re(x)=ℜ(x)

$$\mathrm{Im}\left({x}\right)=\Im\left({x}\right) \\ $$$$\mathrm{Re}\left({x}\right)=\Re\left({x}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com