
Question and Answers Forum
Question Number 113738 by bemath last updated on 15/Sep/20
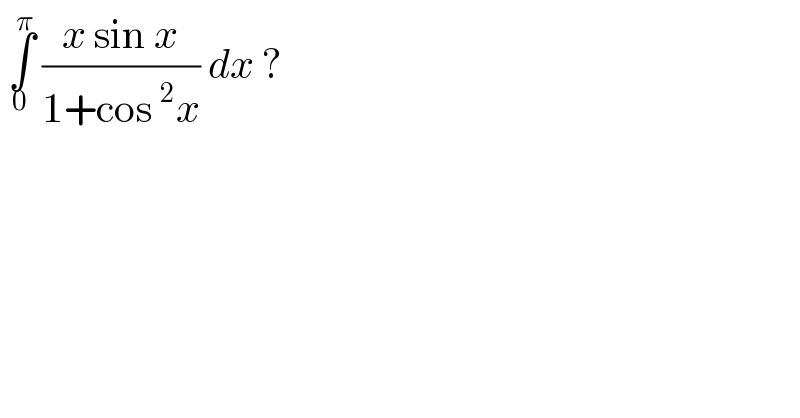
Answered by bobhans last updated on 15/Sep/20
![I = ∫_0 ^π ((x sin x)/(1+cos^2 x)) dx replace x by π−x →I=∫_π ^0 (((π−x)sin (π−x))/(1+cos^2 (π−x))) (−dx) I= ∫_0 ^π (((π−x)sin x)/(1+cos^2 x)) dx = ∫_0 ^π ((πsin x)/(1+cos^2 x)) dx−∫_0 ^π ((xsin x)/(1+cos^2 x)) dx 2I = ∫_0 ^π ((π sin x)/(1+cos^2 x)) dx consider ∫ ((π sin x)/(1+cos x))dx = −π∫ ((d(cos x))/(1+cos^2 x)) = −π∫ (du/(1+u^2 )) = −π tan^(−1) (cos x) + c now we have 2I = −π [ tan^(−1) (cos x) ]_0 ^π I = −(π/2)[−(π/4)−(π/4) ]= (π^2 /4).](Q113739.png)
| ||
Question and Answers Forum | ||
Question Number 113738 by bemath last updated on 15/Sep/20 | ||
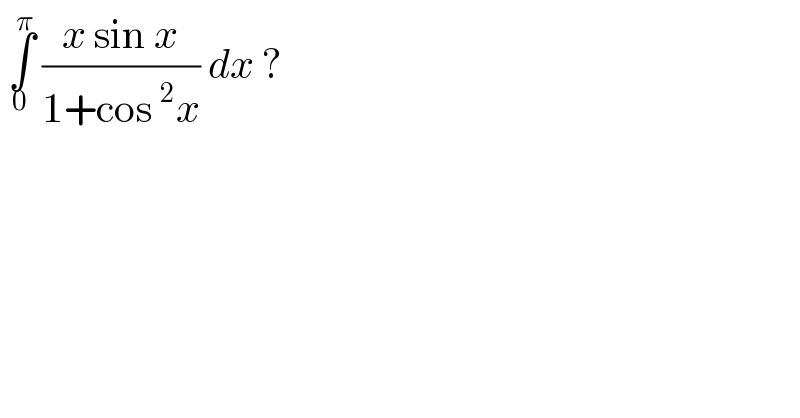 | ||
Answered by bobhans last updated on 15/Sep/20 | ||
![I = ∫_0 ^π ((x sin x)/(1+cos^2 x)) dx replace x by π−x →I=∫_π ^0 (((π−x)sin (π−x))/(1+cos^2 (π−x))) (−dx) I= ∫_0 ^π (((π−x)sin x)/(1+cos^2 x)) dx = ∫_0 ^π ((πsin x)/(1+cos^2 x)) dx−∫_0 ^π ((xsin x)/(1+cos^2 x)) dx 2I = ∫_0 ^π ((π sin x)/(1+cos^2 x)) dx consider ∫ ((π sin x)/(1+cos x))dx = −π∫ ((d(cos x))/(1+cos^2 x)) = −π∫ (du/(1+u^2 )) = −π tan^(−1) (cos x) + c now we have 2I = −π [ tan^(−1) (cos x) ]_0 ^π I = −(π/2)[−(π/4)−(π/4) ]= (π^2 /4).](Q113739.png) | ||
| ||