Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 64112 by mr W last updated on 13/Jul/19

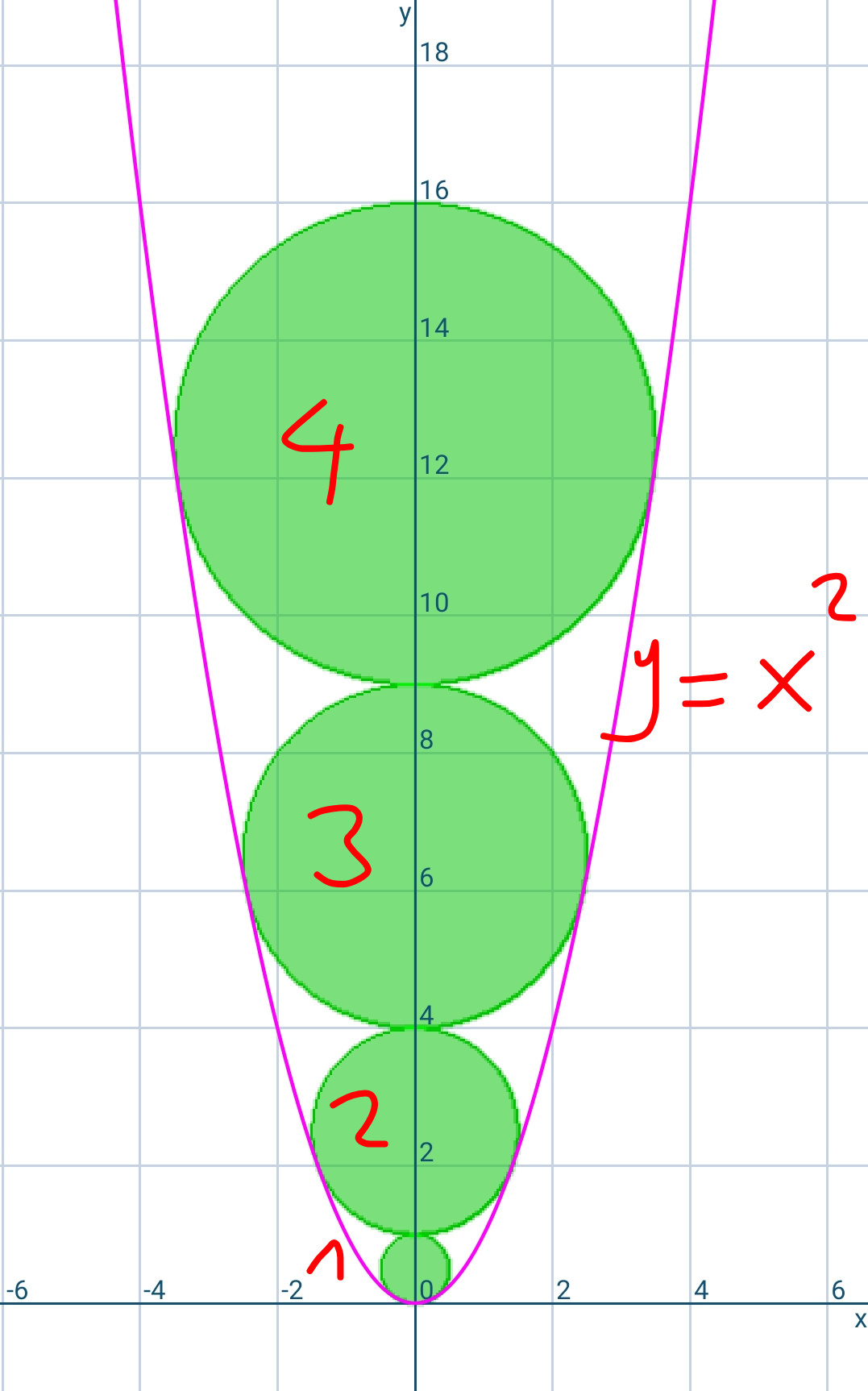
Commented by mr W last updated on 13/Jul/19

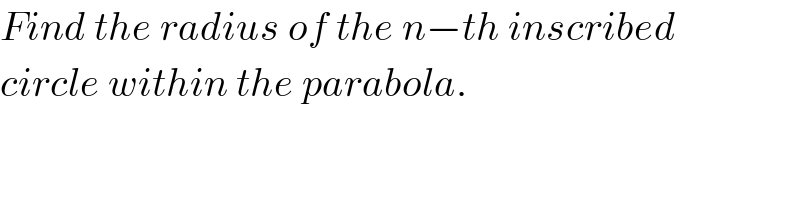
$F i n d t h e r a d i u s o f t h e n - t h i n s c r i b e d$ $c i r c l e w i t h i n t h e p a r a b o l a .$
	Answered by ajfour last updated on 13/Jul/19

	$x^{2} + {(y - r_{1})}^{2} = r_{1}^{2}$ $x + \frac{d y}{d x} (y - r_{1}) = 0$ $\frac{d y}{d x} = \frac{x}{r_{1} - y} \Rightarrow \frac{d^{2} y}{{d x}^{2}} = \frac{r_{1} - y + x \frac{d y}{d x}}{{(r_{1} - y)}^{2}}$ $A t o r i g i n w e t h e n h a v e$ $\frac{1}{r_{1}} = 2 \Rightarrow r_{1} = 1 / 2$ $l e t c e n t r e o f n^{t h} c i r c l e b e (0, c_{n})$ $c_{n} = 2 (r_{1} + r_{2} + . . . + r_{n - 1}) + r_{n}$ $l e t t h i s c i r c l e t o u c h p a r a b o l a a t$ $(h, k) .$ $h = r_{n} \sin θ$ $k = c_{n} - r_{n} \cos θ$ $2 r_{n} \sin θ = \tan θ$ $\Rightarrow r_{n} \cos θ = \frac{1}{2}$ $c_{n} - \frac{1}{2} = r_{n}^{2} - \frac{1}{4}$ $\Rightarrow c_{n} = r_{n}^{2} + \frac{1}{4}$ $c_{n} = 2 (r_{1} + r_{2} + . . . + r_{n - 1}) + r_{n}$ $\frac{1}{2} (r_{n}^{2} - r_{n} + \frac{1}{4}) = r_{1} + r_{2} + . . . + r_{n - 1}$ $\frac{1}{2} {(r_{n} - \frac{1}{2})}^{2} = r_{1} + r_{2} + . . . + r_{n - 1}$ $\frac{1}{2} (r_{n + 1} - \frac{1}{2}) = r_{1} + r_{2} + . . + r_{n}$ $\Rightarrow \frac{1}{2} (r_{n + 1} - r_{n}) (r_{n + 1} + r_{n} - 1)$ $= r_{n} - r_{n - 1}$ $\Rightarrow r_{n + 1}^{2} - r_{n + 1} + r_{n} - r_{n}^{2} = 2 r_{n} - 2 r_{n - 1}$ $\Rightarrow r_{n + 1}^{2} - r_{n + 1} = r_{n}^{2} + r_{n} - 2 r_{n - 1}$ $o r {(r_{n + 1} - \frac{1}{2})}^{2} = {(r_{n} + \frac{1}{2})}^{2} - 2 r_{n - 1}$ $w i t h r_{1} = \frac{1}{2} .$
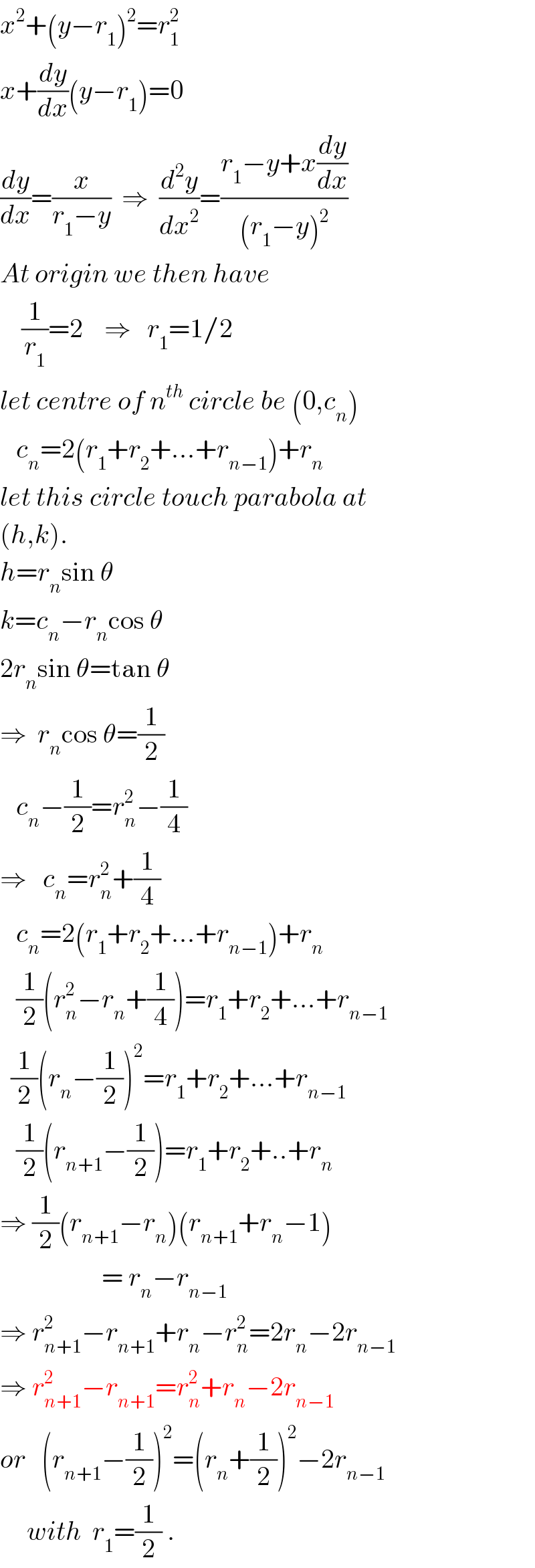
	Commented by mr W last updated on 13/Jul/19

	$t h a n k y o u s i r!$ $a c c . t o d r a w i n g i t s e e m s t h a t$ $r_{n} = n - \frac{1}{2}$ $b u t t h i s {d o e s n}^{'} t m a t c h$ ${(r_{n + 1} - \frac{1}{2})}^{2} = {(r_{n} + \frac{1}{2})}^{2} - 2 r_{n - 1}$ $c a n y o u p l e a s e r e c h e c k ?$
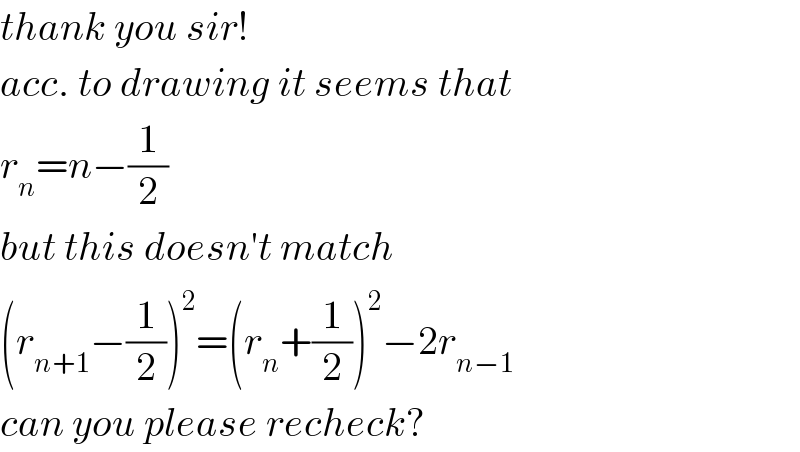
	Answered by mr W last updated on 13/Jul/19

	$f i r s t c i r c l e t o u c h e s t h e p a r a b o l a a t (0, 0)$ $y^{'} = 2 x$ $y^{″} = 2 \Rightarrow R = \frac{1}{2}$ $\Rightarrow r a d i u s o f t h e f i r s t c i r c l e r_{1} = \frac{1}{2}$ $l e t r_{n} = r a d i u s o f n t h c i r c l e$ $d_{n} = d i a m e t e r o f n t h c i r c l e, d_{n} = 2 r_{n}$ $t h e n t h c i r c l e t o u c h e s t h e n - 1 t h c i r c l e$ $a t (0, d_{1} + d_{2} + . . . d_{n - 1})$ $l e t a_{n} = d_{1} + d_{2} + . . . d_{n - 1} = 2 (r_{1} + r_{2} + . . . + r_{n - 1})$ $e q n . o f n t h c i r c l e :$ $x^{2} + {(y - a_{n} - r_{n})}^{2} = r_{n}^{2}$ $i n t e r s e c t i o n w i t h p a r a b o l a y = x^{2} :$ $y + {(y - a_{n} - r_{n})}^{2} = r_{n}^{2}$ $\Rightarrow y^{2} - [2 (a_{n} + r_{n}) - 1] y + a_{n} (a_{n} + 2 r_{n}) = 0$ $d u e t o t a n g e n c y :$ $Δ = {[2 (a_{n} + r_{n}) - 1]}^{2} - 4 a_{n} (a_{n} + 2 r_{n}) = 0$ $4 (a_{n}^{2} + 2 a_{n} r_{n} + r_{n}^{2}) - 4 (a_{n} + r_{n}) + 1 - 4 a_{n}^{2} - 8 a_{n} r_{n} = 0$ $r_{n}^{2} - r_{n} - (a_{n} - \frac{1}{4}) = 0$ $\Rightarrow r_{n} = \frac{1}{2} + \sqrt{a_{n}}$ $\Rightarrow r_{n} = \frac{1}{2} + \sqrt{2 (r_{1} + r_{2} + . . . + r_{n - 1})}$ ${(r_{n} - \frac{1}{2})}^{2} = 2 (r_{1} + r_{2} + . . . + r_{n - 1})$ $\Rightarrow r_{n}^{2} - r_{n} + \frac{1}{4} = 2 (r_{1} + r_{2} + . . . + r_{n - 1}) . . . (i)$ $\Rightarrow r_{n - 1}^{2} - r_{n - 1} + \frac{1}{4} = 2 (r_{1} + r_{2} + . . . + r_{n - 2})$ $\Rightarrow r_{n - 1}^{2} + r_{n - 1} + \frac{1}{4} = 2 (r_{1} + r_{2} + . . . + r_{n - 1}) . . . (i i)$ $(i) - (i i) :$ $(r_{n} + r_{n - 1}) (r_{n} - r_{n - 1} - 1) = 0$ $\Rightarrow r_{n} - r_{n - 1} - 1 = 0$ $\Rightarrow r_{n} - r_{n - 1} = 1$ $\Rightarrow r_{1}, r_{2}, r_{3}, . ., r_{n} a r e A . P . w i t h c o m m o n$ $d i f f e r e n c e 1, s i n c e r_{1} = \frac{1}{2},$ $\Rightarrow r_{n} = \frac{1}{2} + (n - 1) \times 1 = n - \frac{1}{2}$
	Commented by ajfour last updated on 13/Jul/19

	$N i c e t h o u g h t s i r, g e t t i n g r i d o f r_{n - 2}!$ $Y o u h a d s o l v e d i t b e f o r e, t h o u g h$ $n o t t h i s r i g o r o u s w a y .$
	Commented by mr W last updated on 13/Jul/19

	$t o b e h o n e s t i f o u n d a t f i r s t o n l y t h e$ $r e l a t i o n r = \frac{1}{2} + \sqrt{a} a n d d r e w t h e c i r c l e s$ $o n e a f t e r o n e . a f t e r i h a v e p o s t e d t h e q u e s t i o n,$ $i f o u n d t h a t t h e c i r c l e s t o u c h e a c h o t h e r$ $a l w a y s a t p e r f e c t s q u a r e s 1, 4, 9, 16 . . .$ $t h a t m e a n s t h e r a d i i a r e a n A . P .$ $a f t e r i h a v e r e a d y o u r p o s t i t r i e d t o f i n d$ $a w a y t o p r o v e t h i s . i f o u n d a w a y a f t e r$ $s o m e t r i a l s .$
	Commented by Tawa11 last updated on 04/Jan/22

	$I just see this . God bless you sir .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum