
Question and Answers Forum
Question Number 64119 by ajfour last updated on 13/Jul/19

Commented by ajfour last updated on 13/Jul/19

Answered by ajfour last updated on 14/Jul/19
![p :radius of circle with center A q : center B ; r : center C and R : radius of central circle q+r=a r+p=b p+q=c p+q+r=s p=s−a , q=s−b , r=s−c let center of small circle be (0,k_A ) (x+q)^2 +y^2 =(q+R)^2 (x−r)^2 +y^2 =(r+R)^2 ⇒ (2x+q−r)(q+r)=(q−r)(q+r+2R) ⇒ 2x=(((q−r)(q+r+2R))/(q+r))−(q−r) x=(((q−r)R)/(q+r)) y^2 =(q+R)^2 −(q+(((q−r)R)/(q+r)))^2 y^2 =[q+R+q+(((q−r)R)/(q+r))][R−(((q−r)R)/(q+r))] y^2 =((4qrR)/(q+r))[1+(R/(q+r))] k_A =(√(((4qrR)/(q+r))(1+(R/(q+r))))) ⇒ k_A =(2/a)(√(qrR(a+R))) let Area of △ABC be △. △=((ak_A +bk_B +ck_C )/2) ⇒ (√(qrR(a+R)))+(√(rpR(b+R)))+ +(√(pqR(c+R))) = △ ....](Q64131.png)
Answered by ajfour last updated on 15/Jul/19
![let center of central circle be (h,k) and radius ρ. let B be origin. h^2 +k^2 =(q+ρ)^2 (h−q−r)^2 +k^2 =(r+ρ)^2 ⇒(q+r)[2h−(q+r)]=(q−r)(q+r+2ρ) 2h=(((q−r)(2ρ+q+r))/(q+r))+q+r h =((ρ(q−r))/(q+r))+q k^2 =(q+ρ)^2 −[((ρ(q−r))/(q+r))+q]^2 k^2 =ρ^2 +2qρ−((ρ^2 (q−r)^2 )/((q+r)^2 ))−((2qρ(q−r))/(q+r)) =((4qrρ^2 )/((q+r)^2 ))+((4qrρ)/((q+r))) = ((4qrρ[ρ+(q+r)])/((q+r)^2 )) let A(x_A , y_A ) x_A =(p+q)cos B y_B =(p+q)sin B [h−(p+q)cos B]^2 +[k−(p+q)sin B]^2 =(p+ρ)^2 ⇒ (q+ρ)^2 +(p+q)^2 −(ρ+p)^2 = 2(p+q)[hcos B+ksin B] ⇒ [((q^2 +qρ+pq−pρ)/(p+q))−hcos B]^2 =k^2 sin^2 B ⇒ [((q^2 +qρ+pq−pρ)/(p+q))−(((ρ(q−r))/(q+r))+q)cos B]^2 =((4qrρ[ρ+(q+r)])/((q+r)^2 ))sin^2 B ⇒[((ρ(q−p))/c)−((ρ(q−r)cos B)/a)+q(1−cos B)]^2 =((4qrρ^2 )/a^2 )sin^2 B+((4qrρ)/a)sin^2 B ⇒ quadratic in ρ ; one is radius of circumcircle of the three circles, and the other the radius of required central one. ⇒ [(A−B)ρ+C]^2 =Dρ^2 +Eρ [(A−B)^2 −D]ρ^2 +[2C(A−B)−E]ρ+C^2 =0 ρ=((−2C(A−B)+E−(√(−4C(A−B)+E^2 +4C^2 D)))/(2[(A−B)^2 −D])) ρ =((−2q(1−cos B)[((q−p)/c)−(((q−r))/a)cos B]+((4qr)/a)sin^2 B−(√(−4q(1−cos B)[((q−p)/c)−(((q−r))/a)cos B]+((16q^2 r^2 )/a^2 )sin^4 B+4q^2 (1−cos B)^2 (((4qr)/a^2 )sin^2 B))))/(2[((q−p)/c)−(((q−r))/a)cos B]^2 −((8qr)/a^2 )sin^2 B)) with cos B = ((c^2 +a^2 −b^2 )/(2ac)) and p=s−a , q=s−b , r=s−c ■](Q64137.png)
Commented by ajfour last updated on 15/Jul/19

Commented by mr W last updated on 15/Jul/19
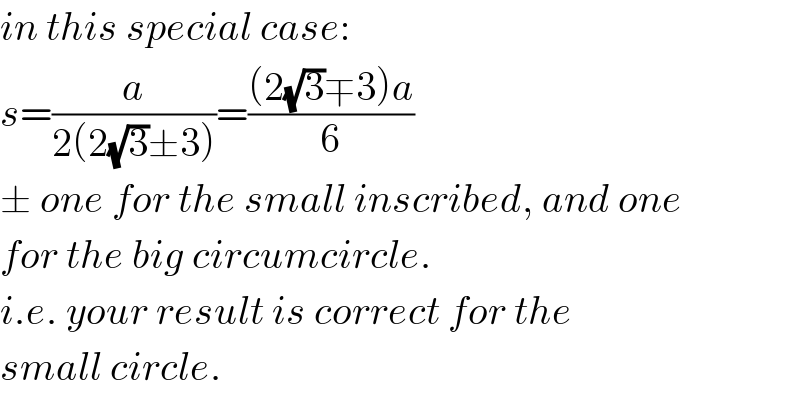
Commented by ajfour last updated on 15/Jul/19

Commented by ajfour last updated on 15/Jul/19

Commented by mr W last updated on 16/Jul/19
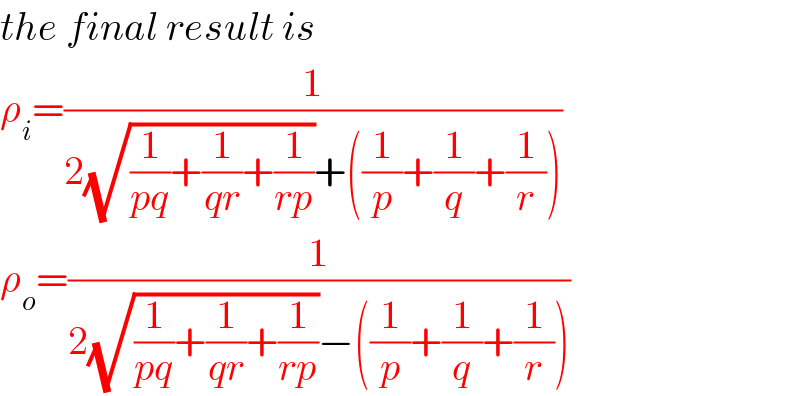
Answered by mr W last updated on 15/Jul/19
![a=q+r b=r+p c=p+q s=a+b+c ⇒p=s−a ⇒q=s−b ⇒r=s−c center of inscribed circle M MA=p+R MB=q+R MC=r+R cos θ_A =((MB^2 +MC^2 −a^2 )/(2MB×MC))=(((q+R)^2 +(r+R)^2 −a^2 )/(2(q+R)(r+R))) cos θ_B =(((r+R)^2 +(p+R)^2 −b^2 )/(2(r+R)(p+R))) cos θ_C =(((p+R)^2 +(q+R)^2 −c^2 )/(2(p+R)(q+R))) θ_A +θ_B +θ_C =2π cos (θ_A +θ_B )=cos (2π−θ_C ) (((q+R)^2 +(r+R)^2 −a^2 )/(2(q+R)(r+R)))×(((r+R)^2 +(p+R)^2 −b^2 )/(2(r+R)(p+R)))−((√({[2(q+R)(r+R)]^2 −[(q+R)^2 +(r+R)^2 −a^2 ]^2 }{[2(r+R)(p+R)]^2 −[(r+R)^2 +(p+R)^2 −b^2 ]^2 }))/(2(q+R)(r+R)2(r+R)(p+R)))=(((p+R)^2 +(q+R)^2 −c^2 )/(2(p+R)(q+R))) (({2R^2 +2(q+r)R+q^2 +r^2 −a^2 }{2R^2 +2(r+p)R+r^2 +p^2 −b^2 }−(√({[2(q+R)(r+R)]^2 −[(q+R)^2 +(r+R)^2 −a^2 ]^2 }{[2(r+R)(p+R)]^2 −[(r+R)^2 +(p+R)^2 −b^2 ]^2 })))/(2(r+R)^2 ))=2R^2 +2(p+q)R+p^2 +q^2 −c^2 {2R^2 +2(q+r)R+q^2 +r^2 −a^2 }{2R^2 +2(r+p)R+r^2 +p^2 −b^2 }−(√({(q+r+2R)^2 −a^2 }{a^2 −(q−r)^2 }{(r+p+2R)^2 −b^2 }{b^2 −(r−p)^2 }))=2(r+R)^2 {2R^2 +2(p+q)R+p^2 +q^2 −c^2 } {2R^2 +2(q+r)R+q^2 +r^2 −a^2 }{2R^2 +2(r+p)R+r^2 +p^2 −b^2 }−(√((q+r+2R+a)(q+r+2R−a)4qr(r+p+2R+b)(r+p+2R−b)4rp))=2(r+R)^2 {2R^2 +2(p+q)R+p^2 +q^2 −c^2 } {2R^2 +2(q+r)R−2qr}{2R^2 +2(r+p)R−2rp}−16Rr(√(pq(R+a)(R+b)))=2(r+R)^2 {2R^2 +2(p+q)R−2pq} {R^2 +(q+r)R−qr}{R^2 +(r+p)R−rp}−4Rr(√(pq(R+a)(R+b)))=(R^2 +2rR+r^2 ){R^2 +(p+q)R−pq} R^4 +(q+r)R^3 −qrR^2 +(r+p)R^3 +(q+r)(r+p)R^2 −qr(r+p)R−rpR^2 −rp(q+r)R+pqr^2 −4Rr(√(pq(R+a)(R+b)))=R^4 +2rR^3 +r^2 R^2 +(p+q)R^3 +2r(p+q)R^2 +r^2 (p+q)R−pqR^2 −2pqrR−pqr^2 (pq−qr−rp)R^2 −(p+q)r^2 R+pqr^2 =2Rr(√(pq(R+q+r)(R+r+p))) .....](Q64154.png)
Commented by ajfour last updated on 15/Jul/19
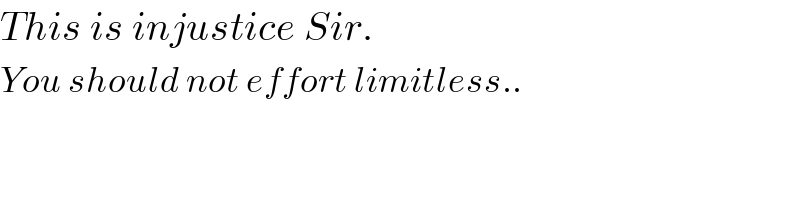
Commented by mr W last updated on 14/Jul/19

