
Question and Answers Forum
Question Number 64139 by Chi Mes Try last updated on 14/Jul/19
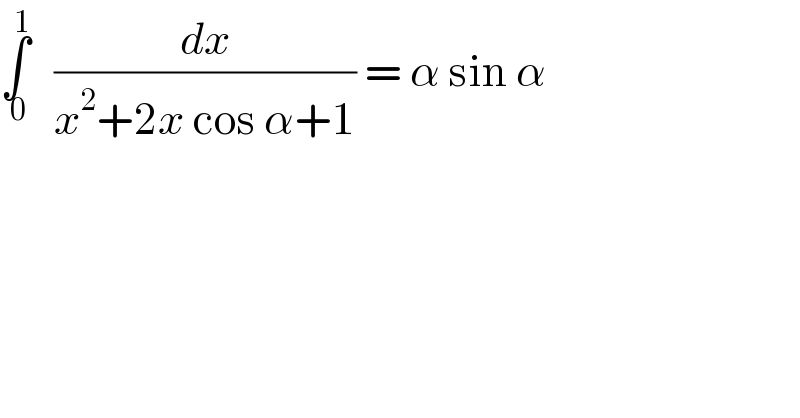
Commented by Prithwish sen last updated on 14/Jul/19
![∫_0 ^1 (dx/((x+cosα)^2 +(sinα)^2 )) =[(1/((sinα))).tan^(−1) (((x+cos)/(sinα)))]_0 ^1](Q64142.png)
Commented by mathmax by abdo last updated on 14/Jul/19
![let I =∫_0 ^1 (dx/(x^2 +2xcosα +1)) ⇒I =∫_0 ^1 (dx/(x^2 +2xcosα +cos^2 α +sin^2 α)) =∫_0 ^1 (dx/((x+cosα)^2 +sin^2 α)) changement x+cosα =sinα t give I = ∫_(cotanα) ^((1+cosα)/(sinα)) ((sinα dt)/(sin^2 α(1+t^2 ))) =(1/(sinα))[arctant]_(1/(tanα)) ^((1+cosα)/(sinα)) =(1/(sinα)){ arctan(((1+cosα)/(sinα)))−arctan((1/(tanα)))but ((1+cosα)/(sinα)) =((2cos^2 ((α/2)))/(2sin((α/2))cos((α/2)))) =(1/(tan((α/2)))) ⇒ arctan(((1+cosα)/(sinα)))=+^− (π/2) −(α/2) arctan((1/(tanα)))=+^− (π/2) −α ⇒ I =(1/(sinα)){+^− (π/2) +^− (π/2) +(α/2)} so there is a error in the question if not a equation...](Q64145.png)
Answered by Hope last updated on 15/Jul/19
![D_r =(x+cosα)^2 +sin^2 α t=x+cosα ∫_(cosα) ^(1+cosα) (dt/(t^2 +sin^2 α)) (1/(sinα))∣tan^(−1) ((t/(sinα)))∣_(cosα) ^(1+cosα) =(1/(sinα))[tan^(−1) (((1+cosα)/(sinα)))−tan^(−1) (((cosα)/(sinα)))] =(1/(sinα))[tan^(−1) (cot(α/2))−tan^(−1) (cotα)] =(1/(sinα))[tan^(−1) (tan((π/2)−(α/2)))−tan^(−1) ((π/2)−α)] =(1/(sinα))[(π/2)−(α/2)−(π/2)+α] =(α/(2sinα))](Q64190.png)
| ||
Question and Answers Forum | ||
Question Number 64139 by Chi Mes Try last updated on 14/Jul/19 | ||
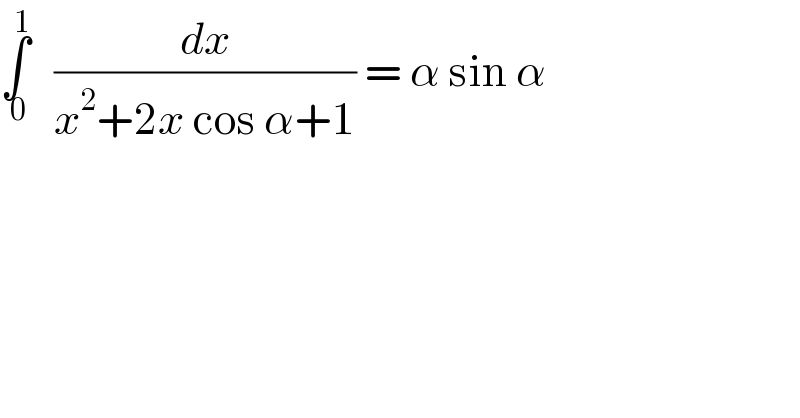 | ||
Commented by Prithwish sen last updated on 14/Jul/19 | ||
![∫_0 ^1 (dx/((x+cosα)^2 +(sinα)^2 )) =[(1/((sinα))).tan^(−1) (((x+cos)/(sinα)))]_0 ^1](Q64142.png) | ||
Commented by mathmax by abdo last updated on 14/Jul/19 | ||
![let I =∫_0 ^1 (dx/(x^2 +2xcosα +1)) ⇒I =∫_0 ^1 (dx/(x^2 +2xcosα +cos^2 α +sin^2 α)) =∫_0 ^1 (dx/((x+cosα)^2 +sin^2 α)) changement x+cosα =sinα t give I = ∫_(cotanα) ^((1+cosα)/(sinα)) ((sinα dt)/(sin^2 α(1+t^2 ))) =(1/(sinα))[arctant]_(1/(tanα)) ^((1+cosα)/(sinα)) =(1/(sinα)){ arctan(((1+cosα)/(sinα)))−arctan((1/(tanα)))but ((1+cosα)/(sinα)) =((2cos^2 ((α/2)))/(2sin((α/2))cos((α/2)))) =(1/(tan((α/2)))) ⇒ arctan(((1+cosα)/(sinα)))=+^− (π/2) −(α/2) arctan((1/(tanα)))=+^− (π/2) −α ⇒ I =(1/(sinα)){+^− (π/2) +^− (π/2) +(α/2)} so there is a error in the question if not a equation...](Q64145.png) | ||
Answered by Hope last updated on 15/Jul/19 | ||
![D_r =(x+cosα)^2 +sin^2 α t=x+cosα ∫_(cosα) ^(1+cosα) (dt/(t^2 +sin^2 α)) (1/(sinα))∣tan^(−1) ((t/(sinα)))∣_(cosα) ^(1+cosα) =(1/(sinα))[tan^(−1) (((1+cosα)/(sinα)))−tan^(−1) (((cosα)/(sinα)))] =(1/(sinα))[tan^(−1) (cot(α/2))−tan^(−1) (cotα)] =(1/(sinα))[tan^(−1) (tan((π/2)−(α/2)))−tan^(−1) ((π/2)−α)] =(1/(sinα))[(π/2)−(α/2)−(π/2)+α] =(α/(2sinα))](Q64190.png) | ||
| ||