Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 64160 by mathmax by abdo last updated on 14/Jul/19

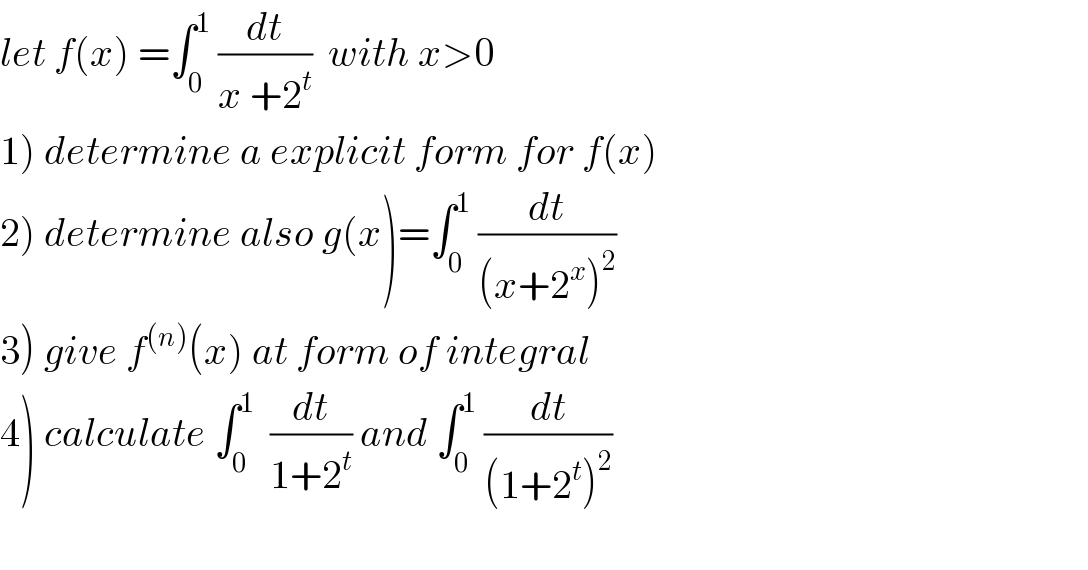
let f(x) =∫_0 ^1 (dt/(x +2^t )) with x>0 1) determine a explicit form for f(x) 2) determine also g(x)=∫_0 ^1 (dt/((x+2^x )^2 )) 3) give f^((n)) (x) at form of integral 4) calculate ∫_0 ^1 (dt/(1+2^t )) and ∫_0 ^1 (dt/((1+2^t )^2 ))

$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{x}\:+\mathrm{2}^{{t}} }\:\:{with}\:{x}>\mathrm{0} \\ $$ $$\left.\mathrm{1}\right)\:{determine}\:{a}\:{explicit}\:{form}\:{for}\:{f}\left({x}\right) \\ $$ $$\left.\mathrm{2}\right)\:{determine}\:{also}\:{g}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\left({x}+\mathrm{2}^{{x}} \right)^{\mathrm{2}} } \\ $$ $$\left.\mathrm{3}\right)\:{give}\:{f}^{\left({n}\right)} \left({x}\right)\:{at}\:{form}\:{of}\:{integral}\: \\ $$ $$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{1}+\mathrm{2}^{{t}} }\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\left(\mathrm{1}+\mathrm{2}^{{t}} \right)^{\mathrm{2}} } \\ $$ $$ \\ $$

Commented bymathmax by abdo last updated on 14/Jul/19

1)we have f(x)=∫_0 ^1 (dt/(x+2^t )) (x>0) changement 2^t =u give e^(tln2) =u ⇒tln(2)=lnu ⇒t=((ln(u))/(ln(2))) ⇒f(x) =∫_1 ^2 (du/(ln(2)u(x+u))) =(1/(ln(2))) (1/x)∫_1 ^2 {(1/u)−(1/(x+u))}du =(1/(xln(2)))[ln((u/(x+u)))]_1 ^2 =(1/(xln(2))){ln((2/(x+2)))−ln((1/(x+1)))}=(1/(xln(2))){ln2−ln(x+2)+ln(x+1)} f(x)=(1/x) +((ln(((x+1)/(x+2))))/(xln(2)))

$$\left.\mathrm{1}\right){we}\:{have}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{{x}+\mathrm{2}^{{t}} }\:\:\:\:\:\left({x}>\mathrm{0}\right)\:{changement}\:\mathrm{2}^{{t}} ={u}\:{give}\: \\ $$ $${e}^{{tln}\mathrm{2}} ={u}\:\Rightarrow{tln}\left(\mathrm{2}\right)={lnu}\:\Rightarrow{t}=\frac{{ln}\left({u}\right)}{{ln}\left(\mathrm{2}\right)}\:\Rightarrow{f}\left({x}\right)\:=\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\frac{{du}}{{ln}\left(\mathrm{2}\right){u}\left({x}+{u}\right)} \\ $$ $$=\frac{\mathrm{1}}{{ln}\left(\mathrm{2}\right)}\:\frac{\mathrm{1}}{{x}}\int_{\mathrm{1}} ^{\mathrm{2}} \left\{\frac{\mathrm{1}}{{u}}−\frac{\mathrm{1}}{{x}+{u}}\right\}{du}\:=\frac{\mathrm{1}}{{xln}\left(\mathrm{2}\right)}\left[{ln}\left(\frac{{u}}{{x}+{u}}\right)\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$ $$=\frac{\mathrm{1}}{{xln}\left(\mathrm{2}\right)}\left\{{ln}\left(\frac{\mathrm{2}}{{x}+\mathrm{2}}\right)−{ln}\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)\right\}=\frac{\mathrm{1}}{{xln}\left(\mathrm{2}\right)}\left\{{ln}\mathrm{2}−{ln}\left({x}+\mathrm{2}\right)+{ln}\left({x}+\mathrm{1}\right)\right\} \\ $$ $${f}\left({x}\right)=\frac{\mathrm{1}}{{x}}\:+\frac{{ln}\left(\frac{{x}+\mathrm{1}}{{x}+\mathrm{2}}\right)}{{xln}\left(\mathrm{2}\right)} \\ $$

Commented bymathmax by abdo last updated on 14/Jul/19

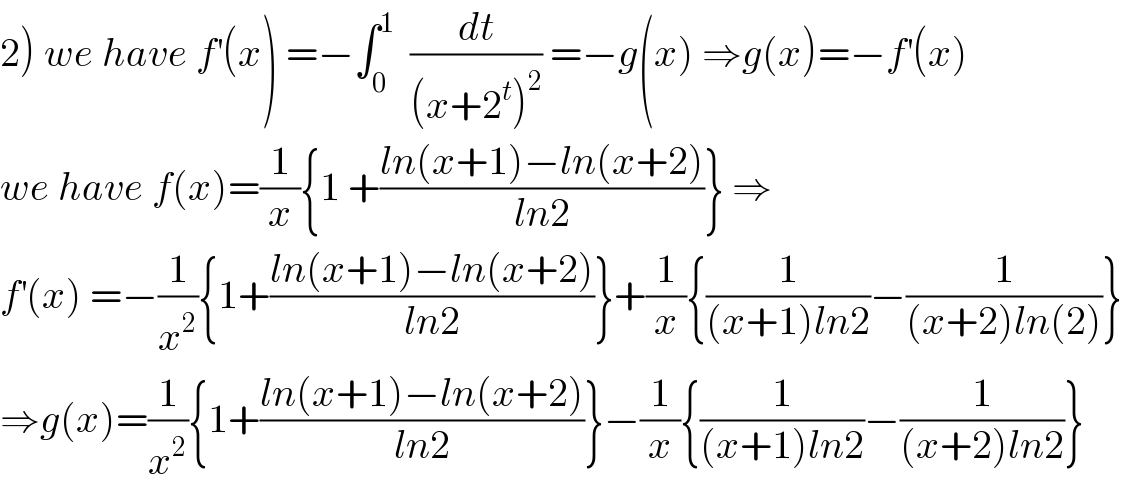
2) we have f^′ (x) =−∫_0 ^1 (dt/((x+2^t )^2 )) =−g(x) ⇒g(x)=−f^′ (x) we have f(x)=(1/x){1 +((ln(x+1)−ln(x+2))/(ln2))} ⇒ f^′ (x) =−(1/x^2 ){1+((ln(x+1)−ln(x+2))/(ln2))}+(1/x){(1/((x+1)ln2))−(1/((x+2)ln(2)))} ⇒g(x)=(1/x^2 ){1+((ln(x+1)−ln(x+2))/(ln2))}−(1/x){(1/((x+1)ln2))−(1/((x+2)ln2))}

$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\left({x}+\mathrm{2}^{{t}} \right)^{\mathrm{2}} }\:=−{g}\left({x}\right)\:\Rightarrow{g}\left({x}\right)=−{f}^{'} \left({x}\right) \\ $$ $${we}\:{have}\:{f}\left({x}\right)=\frac{\mathrm{1}}{{x}}\left\{\mathrm{1}\:+\frac{{ln}\left({x}+\mathrm{1}\right)−{ln}\left({x}+\mathrm{2}\right)}{{ln}\mathrm{2}}\right\}\:\Rightarrow \\ $$ $${f}^{'} \left({x}\right)\:=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left\{\mathrm{1}+\frac{{ln}\left({x}+\mathrm{1}\right)−{ln}\left({x}+\mathrm{2}\right)}{{ln}\mathrm{2}}\right\}+\frac{\mathrm{1}}{{x}}\left\{\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right){ln}\mathrm{2}}−\frac{\mathrm{1}}{\left({x}+\mathrm{2}\right){ln}\left(\mathrm{2}\right)}\right\} \\ $$ $$\Rightarrow{g}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left\{\mathrm{1}+\frac{{ln}\left({x}+\mathrm{1}\right)−{ln}\left({x}+\mathrm{2}\right)}{{ln}\mathrm{2}}\right\}−\frac{\mathrm{1}}{{x}}\left\{\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right){ln}\mathrm{2}}−\frac{\mathrm{1}}{\left({x}+\mathrm{2}\right){ln}\mathrm{2}}\right\} \\ $$

Commented bymathmax by abdo last updated on 14/Jul/19

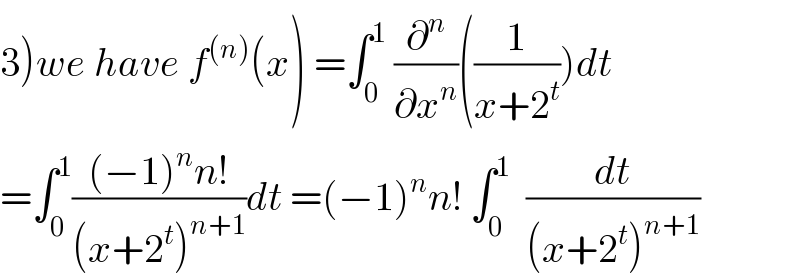
3)we have f^((n)) (x) =∫_0 ^1 (∂^n /∂x^n )((1/(x+2^t )))dt =∫_0 ^1 (((−1)^n n!)/((x+2^t )^(n+1) ))dt =(−1)^n n! ∫_0 ^1 (dt/((x+2^t )^(n+1) ))

$$\left.\mathrm{3}\right){we}\:{have}\:{f}^{\left({n}\right)} \left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\partial^{{n}} }{\partial{x}^{{n}} }\left(\frac{\mathrm{1}}{{x}+\mathrm{2}^{{t}} }\right){dt} \\ $$ $$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({x}+\mathrm{2}^{{t}} \right)^{{n}+\mathrm{1}} }{dt}\:=\left(−\mathrm{1}\right)^{{n}} {n}!\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\left({x}+\mathrm{2}^{{t}} \right)^{{n}+\mathrm{1}} } \\ $$

Commented bymathmax by abdo last updated on 14/Jul/19

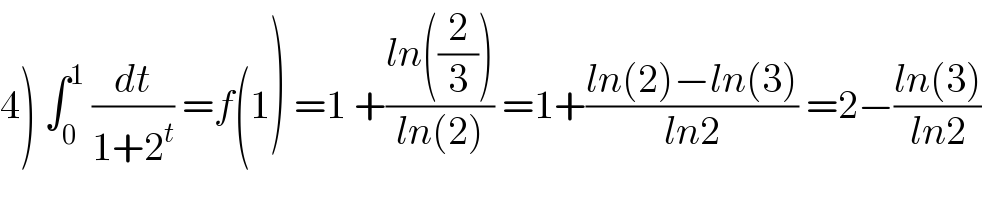
4) ∫_0 ^1 (dt/(1+2^t )) =f(1) =1 +((ln((2/3)))/(ln(2))) =1+((ln(2)−ln(3))/(ln2)) =2−((ln(3))/(ln2))

$$\left.\mathrm{4}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+\mathrm{2}^{{t}} }\:={f}\left(\mathrm{1}\right)\:=\mathrm{1}\:+\frac{{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{{ln}\left(\mathrm{2}\right)}\:=\mathrm{1}+\frac{{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{3}\right)}{{ln}\mathrm{2}}\:=\mathrm{2}−\frac{{ln}\left(\mathrm{3}\right)}{{ln}\mathrm{2}} \\ $$

Commented bymathmax by abdo last updated on 14/Jul/19

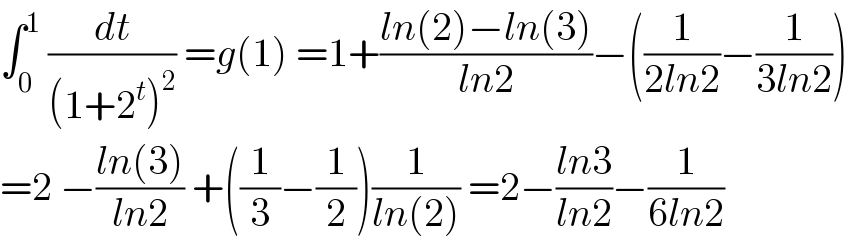
∫_0 ^1 (dt/((1+2^t )^2 )) =g(1) =1+((ln(2)−ln(3))/(ln2))−((1/(2ln2))−(1/(3ln2))) =2 −((ln(3))/(ln2)) +((1/3)−(1/2))(1/(ln(2))) =2−((ln3)/(ln2))−(1/(6ln2))

$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\left(\mathrm{1}+\mathrm{2}^{{t}} \right)^{\mathrm{2}} }\:={g}\left(\mathrm{1}\right)\:=\mathrm{1}+\frac{{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{3}\right)}{{ln}\mathrm{2}}−\left(\frac{\mathrm{1}}{\mathrm{2}{ln}\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}{ln}\mathrm{2}}\right) \\ $$ $$=\mathrm{2}\:−\frac{{ln}\left(\mathrm{3}\right)}{{ln}\mathrm{2}}\:+\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{\mathrm{1}}{{ln}\left(\mathrm{2}\right)}\:=\mathrm{2}−\frac{{ln}\mathrm{3}}{{ln}\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}{ln}\mathrm{2}} \\ $$

Answered by Eminem last updated on 14/Jul/19

1) let u=2^t dt=(du/(uln(2))) f(x)=∫_1 ^2 (du/(uln(2)(x+u)))=∫_1 ^2 (du/(xuln(2)))−∫_1 ^2 (du/(xln(2)(x+u)))=(1/x)−(1/(xln(2)))[ln(x+2)−ln(x+1)]

$$\left.\mathrm{1}\right)\:\:\:\:{let}\:{u}=\mathrm{2}^{{t}} \:\:\:\:\:{dt}=\frac{{du}}{{uln}\left(\mathrm{2}\right)} \\ $$ $${f}\left({x}\right)=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{du}}{{uln}\left(\mathrm{2}\right)\left({x}+{u}\right)}=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{du}}{{xuln}\left(\mathrm{2}\right)}−\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{du}}{{xln}\left(\mathrm{2}\right)\left({x}+{u}\right)}=\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{xln}\left(\mathrm{2}\right)}\left[{ln}\left({x}+\mathrm{2}\right)−{ln}\left({x}+\mathrm{1}\right)\right] \\ $$

Answered by Eminem last updated on 14/Jul/19

2) Same idea its g(x)=∫(dt/((x+2^t )^2 ))? f^((n)) libneiz formula explicite withe integral just swithe derivation withe integral f^n (x)=∫(d/dx^n )(dt/((x+2^t )))=∫(((−1)^n (n)!)/((x+2^t )^(n+1) ))dt 4.put x=1in f(x) 2 nd x=1 in f^′ (x)

$$\left.\mathrm{2}\right)\:{Same}\:{idea}\:{its}\:{g}\left({x}\right)=\int\frac{{dt}}{\left({x}+\mathrm{2}^{{t}} \right)^{\mathrm{2}} }? \\ $$ $${f}^{\left({n}\right)} \:{libneiz}\:{formula}\:{explicite}\: \\ $$ $${withe}\:{integral}\:{just}\:{swithe}\:{derivation}\:{withe}\:{integral} \\ $$ $${f}^{{n}} \left({x}\right)=\int\frac{{d}}{{dx}^{{n}} }\frac{{dt}}{\left({x}+\mathrm{2}^{{t}} \right)}=\int\frac{\left(−\mathrm{1}\right)^{{n}} \left({n}\right)!}{\left({x}+\mathrm{2}^{{t}} \right)^{{n}+\mathrm{1}} }{dt} \\ $$ $$\mathrm{4}.{put}\:\:{x}=\mathrm{1}{in}\:{f}\left({x}\right)\:\mathrm{2}\:{nd}\:{x}=\mathrm{1}\:{in}\:{f}^{'} \left({x}\right) \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com