
Question and Answers Forum
Question Number 64200 by aliesam last updated on 15/Jul/19

Commented by mathmax by abdo last updated on 15/Jul/19
![let I =∫_0 ^1 ((x−1)/(lnx))dx changement lnx=−t give x=e^(−t) I =−∫_0 ^∞ ((e^(−t) −1)/(−t))(−e^(−t) )dt =−∫_0 ^∞ ((e^(−2t) −e^(−t) )/t)dt let introduce the parametric function f(x) =∫_0 ^∞ ((e^(−2t) −e^(−t) )/t) e^(−xt) dt with x>0 we have f^′ (x) =−∫_0 ^∞ (e^(−2t) −e^(−t) )e^(−xt) dt =−∫_0 ^∞ { e^(−(x+2)t) −e^(−(x+1)t) }dt =∫_0 ^∞ (e^(−(x+1)t) −e^(−(x+2)t) )dt =[−(1/(x+1))e^(−(x+1)t) +(1/(x+2))e^(−(x+2)t) ]_0 ^(+∞) =(1/(x+1))−(1/(x+2)) ⇒f(x)=ln(x+1)−ln(x+2)+c=ln(((x+1)/(x+2))) +c ∃m>0 /∣f(x)∣≤m∫_0 ^∞ e^(−xt) dt =(m/x) →0 (x→+∞) c=lim_(x→+∞) (f(x)−ln(((x+1)/(x+2))))=0 f(x)=ln(((x+1)/(x+2))) I =lim_(x→0) −f(x) = ln(2) .](Q64212.png)
Answered by Hope last updated on 15/Jul/19
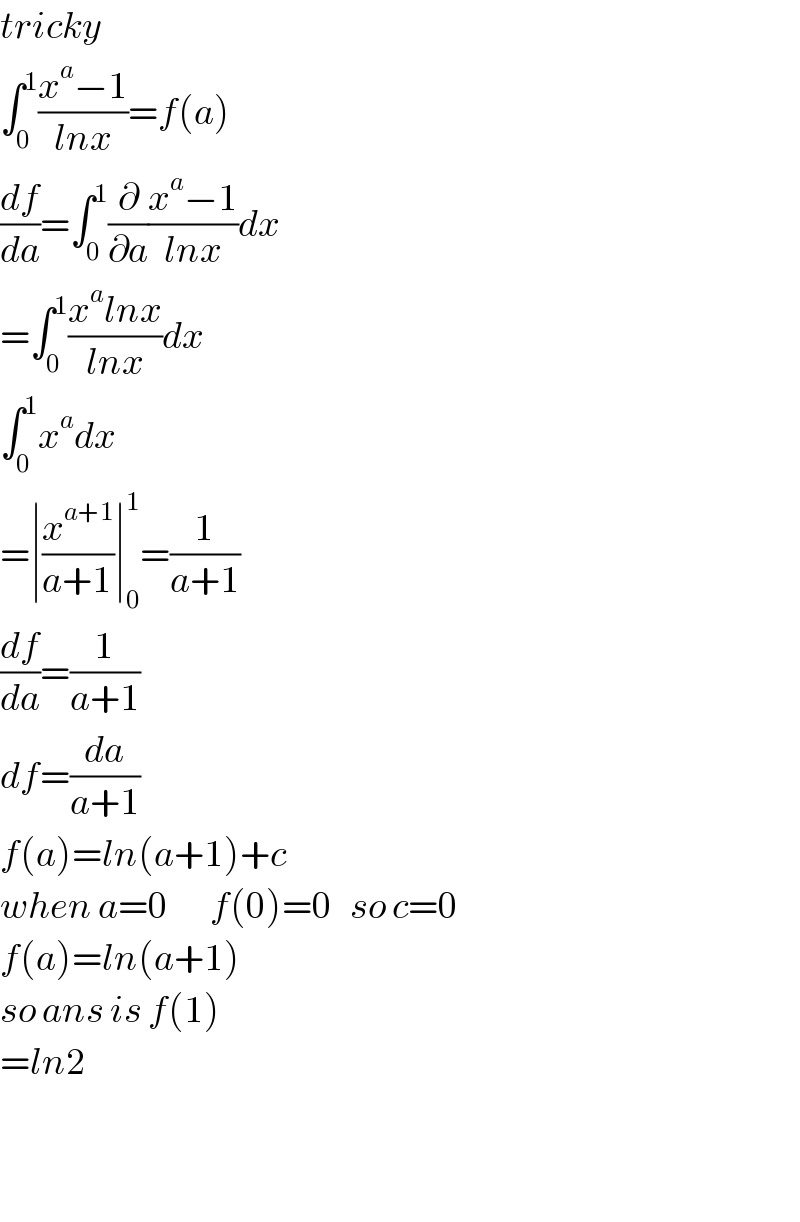
| ||
Question and Answers Forum | ||
Question Number 64200 by aliesam last updated on 15/Jul/19 | ||
 | ||
Commented by mathmax by abdo last updated on 15/Jul/19 | ||
![let I =∫_0 ^1 ((x−1)/(lnx))dx changement lnx=−t give x=e^(−t) I =−∫_0 ^∞ ((e^(−t) −1)/(−t))(−e^(−t) )dt =−∫_0 ^∞ ((e^(−2t) −e^(−t) )/t)dt let introduce the parametric function f(x) =∫_0 ^∞ ((e^(−2t) −e^(−t) )/t) e^(−xt) dt with x>0 we have f^′ (x) =−∫_0 ^∞ (e^(−2t) −e^(−t) )e^(−xt) dt =−∫_0 ^∞ { e^(−(x+2)t) −e^(−(x+1)t) }dt =∫_0 ^∞ (e^(−(x+1)t) −e^(−(x+2)t) )dt =[−(1/(x+1))e^(−(x+1)t) +(1/(x+2))e^(−(x+2)t) ]_0 ^(+∞) =(1/(x+1))−(1/(x+2)) ⇒f(x)=ln(x+1)−ln(x+2)+c=ln(((x+1)/(x+2))) +c ∃m>0 /∣f(x)∣≤m∫_0 ^∞ e^(−xt) dt =(m/x) →0 (x→+∞) c=lim_(x→+∞) (f(x)−ln(((x+1)/(x+2))))=0 f(x)=ln(((x+1)/(x+2))) I =lim_(x→0) −f(x) = ln(2) .](Q64212.png) | ||
Answered by Hope last updated on 15/Jul/19 | ||
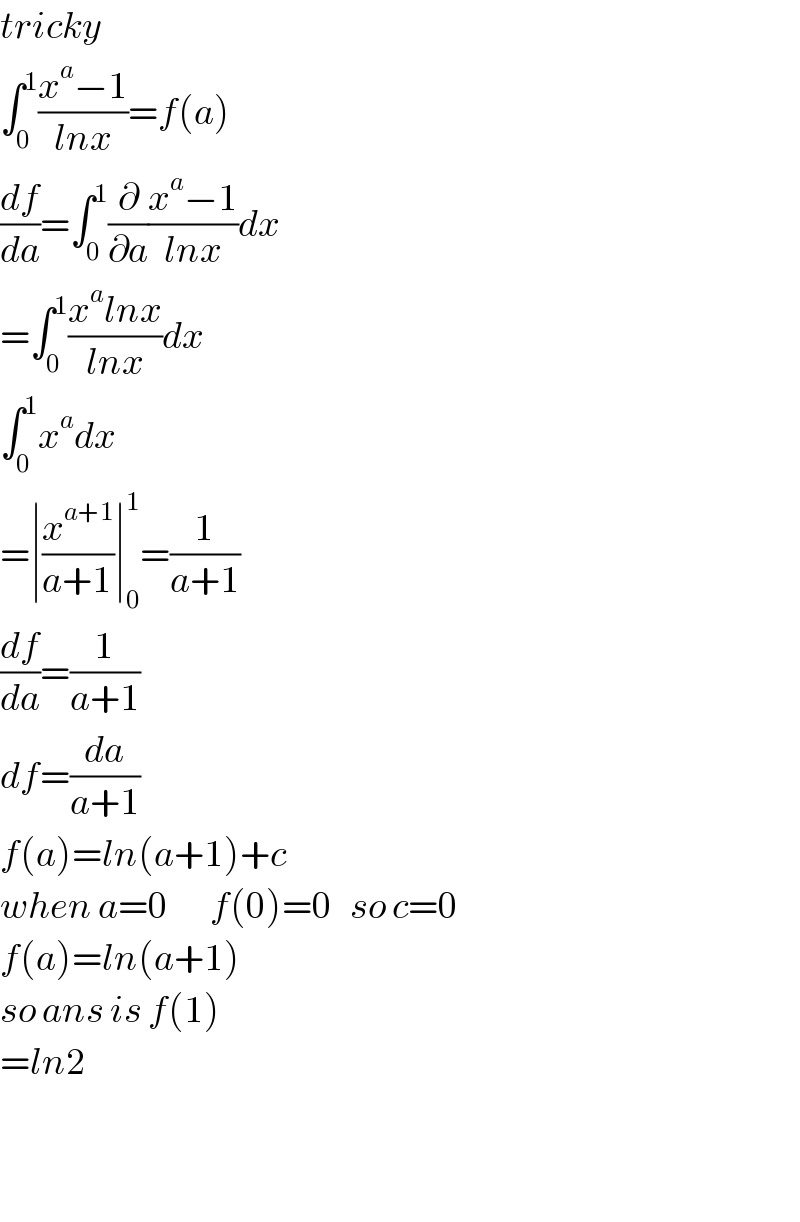 | ||
| ||