Question Number 64201 by Prithwish sen last updated on 15/Jul/19
$$\mathrm{Find}\:\mathrm{all}\:\mathrm{positive}\:\mathrm{solutions}\: \\ $$$$\mathrm{x}+\mathrm{y}+\mathrm{z}\:=\:\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +\:\mathrm{z}^{\mathrm{3}} \:+\:\mathrm{xyz}\:=\:\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{y}^{\mathrm{4}} \:+\:\mathrm{z}^{\mathrm{4}} \:+\mathrm{1} \\ $$
Answered by MJS last updated on 15/Jul/19
$${z}=\mathrm{1}−{x}−{y} \\ $$$$\Rightarrow \\ $$$${y}^{\mathrm{4}} +\mathrm{2}\left({x}−\mathrm{1}\right){y}^{\mathrm{3}} +\frac{\mathrm{6}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{3}}{\mathrm{2}}{y}^{\mathrm{2}} +\frac{\mathrm{4}{x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{1}}{\mathrm{2}}{y}+\frac{\mathrm{2}{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −{x}+\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$${y}={t}−\frac{{x}−\mathrm{1}}{\mathrm{2}} \\ $$$${t}^{\mathrm{4}} +\frac{{x}\left(\mathrm{3}{x}−\mathrm{2}\right)}{\mathrm{2}}{t}^{\mathrm{2}} +\frac{\mathrm{9}{x}^{\mathrm{4}} −\mathrm{12}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +\mathrm{7}}{\mathrm{16}}=\mathrm{0} \\ $$$$\Rightarrow\:{t}^{\mathrm{2}} =−\frac{{x}\left(\mathrm{3}{x}−\mathrm{2}\right)}{\mathrm{4}}\pm\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}\mathrm{i} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{at}\:\mathrm{all} \\ $$
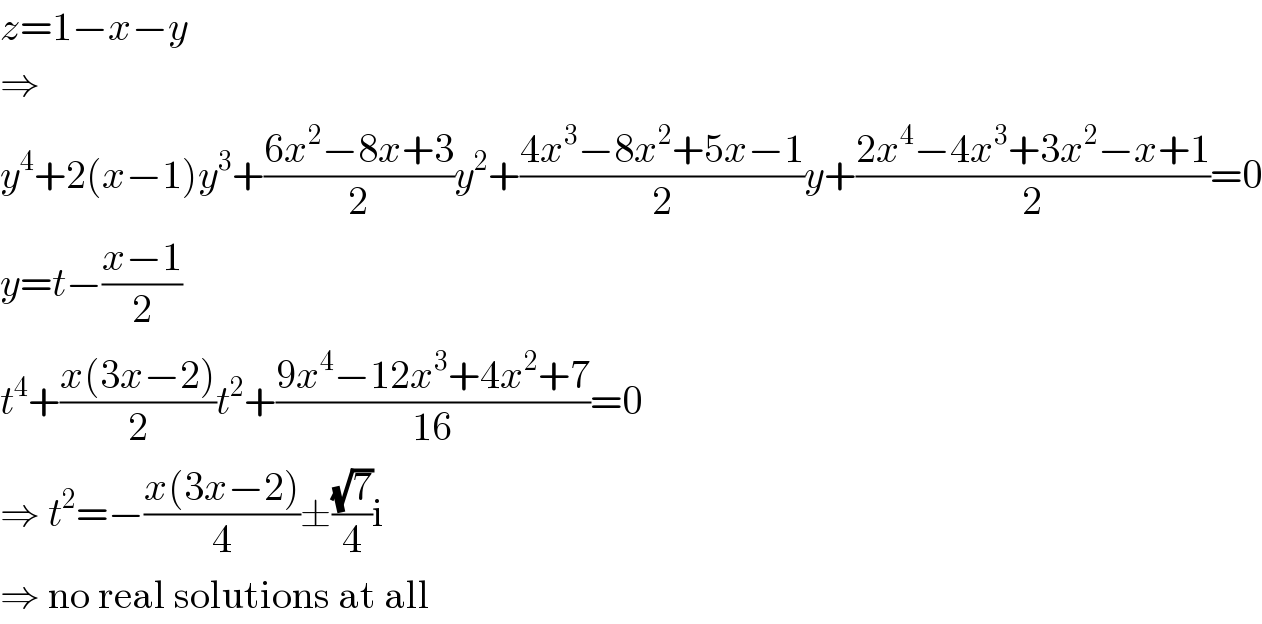
Commented by MJS last updated on 15/Jul/19
$$\mathrm{the}\:\mathrm{maximum}\:\mathrm{of} \\ $$$$−{x}^{\mathrm{4}} −{y}^{\mathrm{4}} −{z}^{\mathrm{4}} −\mathrm{1}+{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} +{xyz} \\ $$$$\mathrm{is}\:−\frac{\mathrm{7}}{\mathrm{8}} \\ $$
Commented by Prithwish sen last updated on 15/Jul/19
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 16/Jul/19
![(x+y+z)^4 =x^4 +(y+z)^4 +4x^3 (y+z) +6x^2 (y+z)^2 +4x(y+z)^3 ⇒ x^4 +y^4 +z^4 +4yz[(y+z)^2 −2yz) +6y^2 z^2 +6x^2 (y+z)^2 +4x(y+z)^3 =1 or since y+z=1−x ⇒ x^4 +y^4 +z^4 −2y^2 z^2 +6x^2 (1−x)^2 +4x(1−x)^3 =1 ________________________ ⇒ 2y^2 z^2 = x^4 +y^4 +z^4 +(2x^2 +4x)(1−x)^2 −1 ________________________ ......(i) (x+y+z)^3 =x^3 +y^3 +z^3 +3[x^2 (y+z)+y^2 (z+x)+z^2 (x+y)] +6xyz ⇒ x^3 +y^3 +z^3 +3x^2 (1−x)+3yz(1−x) +3x(1−2yz)+6xyz=1 ⇒ yz=((x^3 +y^3 +z^3 −3x^3 +3x^2 +3x−1)/(3x−3)) or 3(x−1)yz=x^3 +y^3 +z^3 +(1−x^2 )(3x−1) .......(ii) (i)−(ii) 2y^2 z^2 −3(x−1)yz=xyz−1 +2x(x+2)(1−x)^2 −1−(1−x^2 )(3x−1) ⇒ 2yz(yz+x)+2=(1−x)[−2x^3 −2x^2 +4x−3x^2 −2x+1) ⇒ 2yz(yz+x)+2+ (1−x)(2x^3 +5x^2 −2x−1)=0 say y^2 z^2 +x(yz)+1+f=0 yz=−(x/2)+(√((x^2 /4)−(1+f))) and y+z=1−x ⇒ y, z are roots of eq. s^2 −(1−x)s+(√((x^2 /4)−(1+f)))−(x/2)=0 ⇒ y, z = ((1−x)/2)±(√((((1−x)^2 )/4)+(x/2)−(√((x^2 /4)−(1+f))))) for +ve y and z , x<1 1+f < 0 2+2f=(1−x)(2x^3 +5x^2 −2x−1)+2< 0 ⇒ 2x^4 +3x^3 −7x^2 +x−1> 0 for x∈(0,1) but for no real x is this true, (see graph below)..](Q64228.png)
$$\left({x}+{y}+{z}\right)^{\mathrm{4}} ={x}^{\mathrm{4}} +\left({y}+{z}\right)^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} \left({y}+{z}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{6}{x}^{\mathrm{2}} \left({y}+{z}\right)^{\mathrm{2}} +\mathrm{4}{x}\left({y}+{z}\right)^{\mathrm{3}} \\ $$$$\Rightarrow\:{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +\mathrm{4}{yz}\left[\left({y}+{z}\right)^{\mathrm{2}} −\mathrm{2}{yz}\right) \\ $$$$\:\:+\mathrm{6}{y}^{\mathrm{2}} {z}^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{2}} \left({y}+{z}\right)^{\mathrm{2}} +\mathrm{4}{x}\left({y}+{z}\right)^{\mathrm{3}} =\mathrm{1} \\ $$$$ \\ $$$${or}\:\:{since}\:\:{y}+{z}=\mathrm{1}−{x} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} −\mathrm{2}{y}^{\mathrm{2}} {z}^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:+\mathrm{4}{x}\left(\mathrm{1}−{x}\right)^{\mathrm{3}} =\mathrm{1}\:\:\:\:\:\:\: \\ $$$$\:\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\:\mathrm{2}{y}^{\mathrm{2}} {z}^{\mathrm{2}} =\:{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}\right)\left(\mathrm{1}−{x}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$\:\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:......\left({i}\right) \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{3}} ={x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} \\ $$$$\:+\mathrm{3}\left[{x}^{\mathrm{2}} \left({y}+{z}\right)+{y}^{\mathrm{2}} \left({z}+{x}\right)+{z}^{\mathrm{2}} \left({x}+{y}\right)\right] \\ $$$$\:\:+\mathrm{6}{xyz} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)+\mathrm{3}{yz}\left(\mathrm{1}−{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{3}{x}\left(\mathrm{1}−\mathrm{2}{yz}\right)+\mathrm{6}{xyz}=\mathrm{1} \\ $$$$\Rightarrow\:{yz}=\frac{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{1}}{\mathrm{3}{x}−\mathrm{3}} \\ $$$${or} \\ $$$$\:\:\mathrm{3}\left({x}−\mathrm{1}\right){yz}={x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} +\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{3}{x}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.......\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right) \\ $$$$\mathrm{2}{y}^{\mathrm{2}} {z}^{\mathrm{2}} −\mathrm{3}\left({x}−\mathrm{1}\right){yz}={xyz}−\mathrm{1} \\ $$$$\:\:\:+\mathrm{2}{x}\left({x}+\mathrm{2}\right)\left(\mathrm{1}−{x}\right)^{\mathrm{2}} −\mathrm{1}−\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{3}{x}−\mathrm{1}\right) \\ $$$$\Rightarrow\:\: \\ $$$$\mathrm{2}{yz}\left({yz}+{x}\right)+\mathrm{2}=\left(\mathrm{1}−{x}\right)\left[−\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{2}{yz}\left({yz}+{x}\right)+\mathrm{2}+ \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{1}−{x}\right)\left(\mathrm{2}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${say} \\ $$$$\:\:\:{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{x}\left({yz}\right)+\mathrm{1}+{f}=\mathrm{0} \\ $$$$\:\:\:{yz}=−\frac{{x}}{\mathrm{2}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\left(\mathrm{1}+{f}\right)} \\ $$$$\:\:{and}\:\:\:{y}+{z}=\mathrm{1}−{x} \\ $$$$\Rightarrow \\ $$$$\:\:{y},\:{z}\:{are}\:{roots}\:{of}\:{eq}. \\ $$$$\:\:\:{s}^{\mathrm{2}} −\left(\mathrm{1}−{x}\right){s}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\left(\mathrm{1}+{f}\right)}−\frac{{x}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\:{y},\:{z}\:=\:\frac{\mathrm{1}−{x}}{\mathrm{2}}\pm\sqrt{\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\mathrm{4}}+\frac{{x}}{\mathrm{2}}−\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\left(\mathrm{1}+{f}\right)}} \\ $$$${for}\:+{ve}\:\:\:\:{y}\:{and}\:{z}\:\:,\:\:{x}<\mathrm{1} \\ $$$$\:\:\:\mathrm{1}+{f}\:<\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2}+\mathrm{2}{f}=\left(\mathrm{1}−{x}\right)\left(\mathrm{2}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)+\mathrm{2}<\:\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{2}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{3}} −\mathrm{7}{x}^{\mathrm{2}} +{x}−\mathrm{1}>\:\mathrm{0} \\ $$$$\:\:\:\:{for}\:{x}\in\left(\mathrm{0},\mathrm{1}\right) \\ $$$$\:\:\:\:\:{but}\:{for}\:{no}\:{real}\:{x}\:{is}\:{this}\:{true}, \\ $$$$\:\:\left({see}\:{graph}\:{below}\right).. \\ $$
Commented by ajfour last updated on 16/Jul/19
Commented by Prithwish sen last updated on 16/Jul/19
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir} \\ $$