Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 64204 by naka3546 last updated on 15/Jul/19

Commented by naka3546 last updated on 15/Jul/19

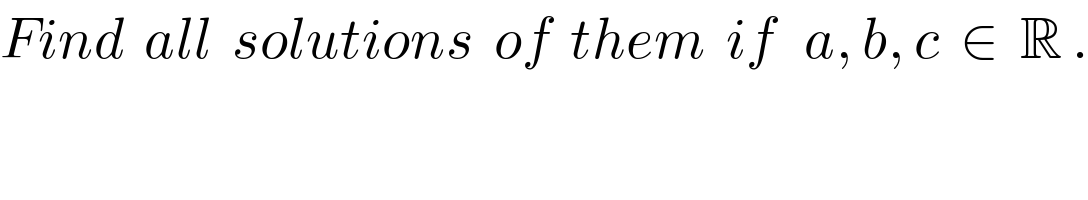
Find all solutions of them if a, b, c ∈ R .

$${Find}\:\:{all}\:\:{solutions}\:\:{of}\:\:{them}\:\:{if}\:\:\:{a},\:{b},\:{c}\:\:\in\:\:\mathbb{R}\:. \\ $$

Answered by MJS last updated on 16/Jul/19

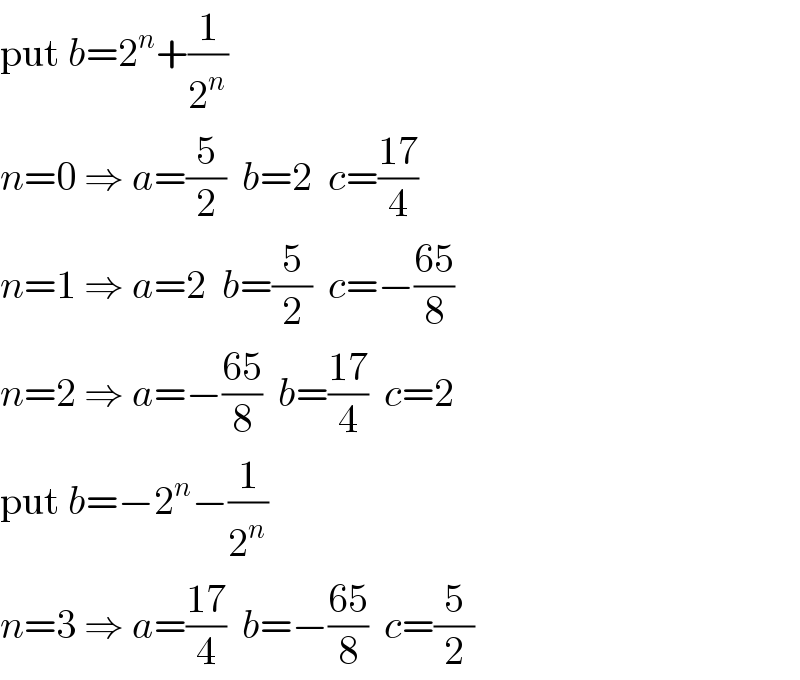
put b=2^n +(1/2^n ) n=0 ⇒ a=(5/2) b=2 c=((17)/4) n=1 ⇒ a=2 b=(5/2) c=−((65)/8) n=2 ⇒ a=−((65)/8) b=((17)/4) c=2 put b=−2^n −(1/2^n ) n=3 ⇒ a=((17)/4) b=−((65)/8) c=(5/2)

$$\mathrm{put}\:{b}=\mathrm{2}^{{n}} +\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$${n}=\mathrm{0}\:\Rightarrow\:{a}=\frac{\mathrm{5}}{\mathrm{2}}\:\:{b}=\mathrm{2}\:\:{c}=\frac{\mathrm{17}}{\mathrm{4}} \\ $$$${n}=\mathrm{1}\:\Rightarrow\:{a}=\mathrm{2}\:\:{b}=\frac{\mathrm{5}}{\mathrm{2}}\:\:{c}=−\frac{\mathrm{65}}{\mathrm{8}} \\ $$$${n}=\mathrm{2}\:\Rightarrow\:{a}=−\frac{\mathrm{65}}{\mathrm{8}}\:\:{b}=\frac{\mathrm{17}}{\mathrm{4}}\:\:{c}=\mathrm{2} \\ $$$$\mathrm{put}\:{b}=−\mathrm{2}^{{n}} −\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$${n}=\mathrm{3}\:\Rightarrow\:{a}=\frac{\mathrm{17}}{\mathrm{4}}\:\:{b}=−\frac{\mathrm{65}}{\mathrm{8}}\:\:{c}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$

Commented by ajfour last updated on 16/Jul/19

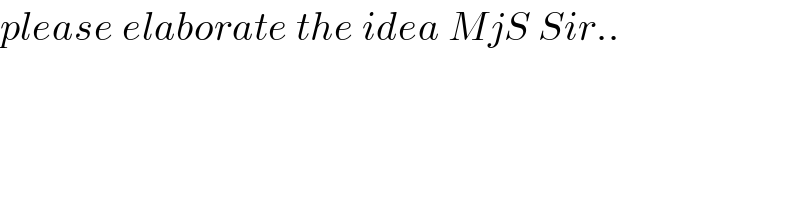
please elaborate the idea MjS Sir..

$${please}\:{elaborate}\:{the}\:{idea}\:{MjS}\:{Sir}.. \\ $$

Commented by MJS last updated on 16/Jul/19

the idea came at night by discovering the solutions I found by trying different paths had this structure, and looking at the right handed constants 3=((2^2 −1)/2^0 ) ((15)/2)=((2^4 −1)/2^1 ) ((63)/4)=((2^6 −1)/2^2 ) (5/2)=((2^2 +1)/2^1 )=2^1 +(1/2^1 ) ((17)/4)=((2^4 +1)/2^2 )=2^2 +(1/2^2 ) ((65)/8)=((2^6 +1)/2^3 )=2^3 +(1/2^3 ) and 2 can be written as 2^0 +(1/2^0 )

$$\mathrm{the}\:\mathrm{idea}\:\mathrm{came}\:\mathrm{at}\:\mathrm{night}\:\mathrm{by}\:\mathrm{discovering}\:\mathrm{the} \\ $$$$\mathrm{solutions}\:\mathrm{I}\:\mathrm{found}\:\mathrm{by}\:\mathrm{trying}\:\mathrm{different}\:\mathrm{paths} \\ $$$$\mathrm{had}\:\mathrm{this}\:\mathrm{structure},\:\mathrm{and}\:\mathrm{looking}\:\mathrm{at}\:\mathrm{the}\:\mathrm{right} \\ $$$$\mathrm{handed}\:\mathrm{constants} \\ $$$$\mathrm{3}=\frac{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}^{\mathrm{0}} } \\ $$$$\frac{\mathrm{15}}{\mathrm{2}}=\frac{\mathrm{2}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}^{\mathrm{1}} } \\ $$$$\frac{\mathrm{63}}{\mathrm{4}}=\frac{\mathrm{2}^{\mathrm{6}} −\mathrm{1}}{\mathrm{2}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{5}}{\mathrm{2}}=\frac{\mathrm{2}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }=\mathrm{2}^{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} } \\ $$$$\frac{\mathrm{17}}{\mathrm{4}}=\frac{\mathrm{2}^{\mathrm{4}} +\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }=\mathrm{2}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{65}}{\mathrm{8}}=\frac{\mathrm{2}^{\mathrm{6}} +\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }=\mathrm{2}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} } \\ $$$$\mathrm{and}\:\mathrm{2}\:\mathrm{can}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as}\:\mathrm{2}^{\mathrm{0}} +\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} } \\ $$

Commented by MJS last updated on 16/Jul/19

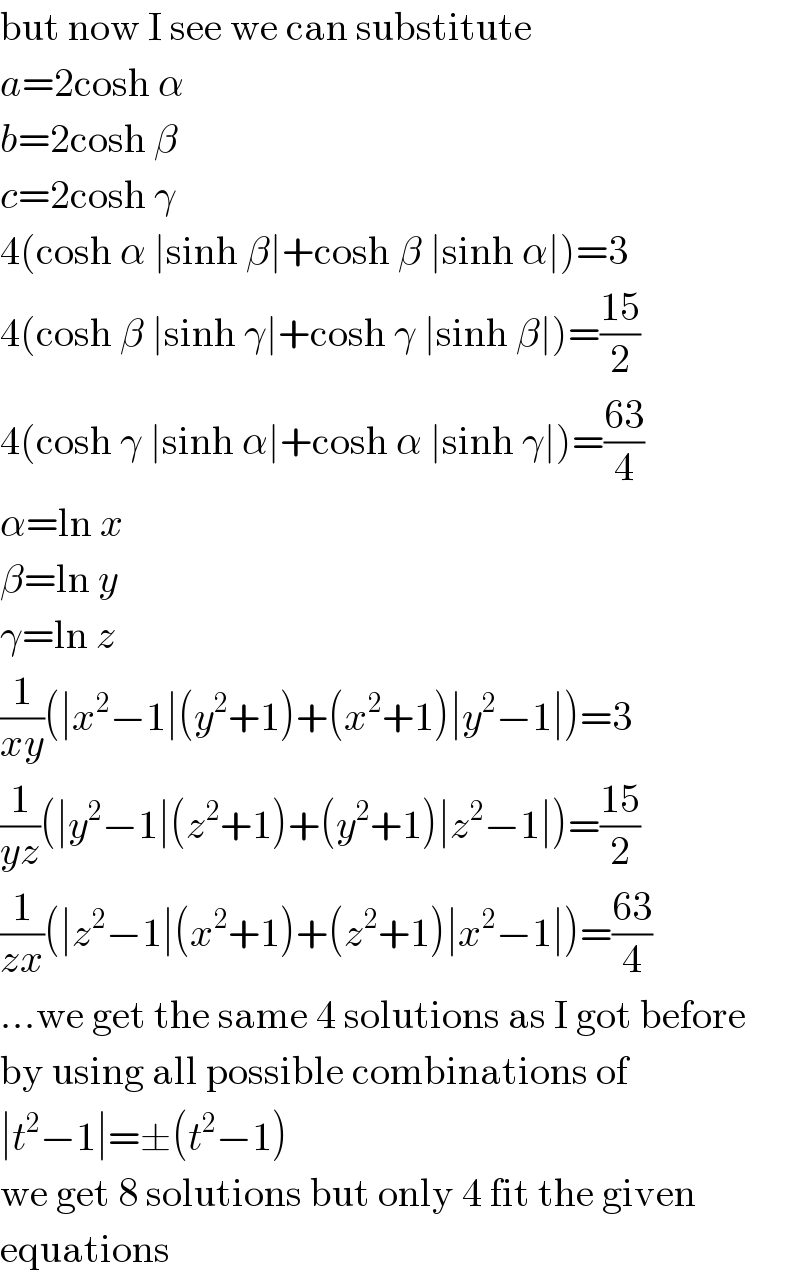
but now I see we can substitute a=2cosh α b=2cosh β c=2cosh γ 4(cosh α ∣sinh β∣+cosh β ∣sinh α∣)=3 4(cosh β ∣sinh γ∣+cosh γ ∣sinh β∣)=((15)/2) 4(cosh γ ∣sinh α∣+cosh α ∣sinh γ∣)=((63)/4) α=ln x β=ln y γ=ln z (1/(xy))(∣x^2 −1∣(y^2 +1)+(x^2 +1)∣y^2 −1∣)=3 (1/(yz))(∣y^2 −1∣(z^2 +1)+(y^2 +1)∣z^2 −1∣)=((15)/2) (1/(zx))(∣z^2 −1∣(x^2 +1)+(z^2 +1)∣x^2 −1∣)=((63)/4) ...we get the same 4 solutions as I got before by using all possible combinations of ∣t^2 −1∣=±(t^2 −1) we get 8 solutions but only 4 fit the given equations

$$\mathrm{but}\:\mathrm{now}\:\mathrm{I}\:\mathrm{see}\:\mathrm{we}\:\mathrm{can}\:\mathrm{substitute} \\ $$$${a}=\mathrm{2cosh}\:\alpha \\ $$$${b}=\mathrm{2cosh}\:\beta \\ $$$${c}=\mathrm{2cosh}\:\gamma \\ $$$$\mathrm{4}\left(\mathrm{cosh}\:\alpha\:\mid\mathrm{sinh}\:\beta\mid+\mathrm{cosh}\:\beta\:\mid\mathrm{sinh}\:\alpha\mid\right)=\mathrm{3} \\ $$$$\mathrm{4}\left(\mathrm{cosh}\:\beta\:\mid\mathrm{sinh}\:\gamma\mid+\mathrm{cosh}\:\gamma\:\mid\mathrm{sinh}\:\beta\mid\right)=\frac{\mathrm{15}}{\mathrm{2}} \\ $$$$\mathrm{4}\left(\mathrm{cosh}\:\gamma\:\mid\mathrm{sinh}\:\alpha\mid+\mathrm{cosh}\:\alpha\:\mid\mathrm{sinh}\:\gamma\mid\right)=\frac{\mathrm{63}}{\mathrm{4}} \\ $$$$\alpha=\mathrm{ln}\:{x} \\ $$$$\beta=\mathrm{ln}\:{y} \\ $$$$\gamma=\mathrm{ln}\:{z} \\ $$$$\frac{\mathrm{1}}{{xy}}\left(\mid{x}^{\mathrm{2}} −\mathrm{1}\mid\left({y}^{\mathrm{2}} +\mathrm{1}\right)+\left({x}^{\mathrm{2}} +\mathrm{1}\right)\mid{y}^{\mathrm{2}} −\mathrm{1}\mid\right)=\mathrm{3} \\ $$$$\frac{\mathrm{1}}{{yz}}\left(\mid{y}^{\mathrm{2}} −\mathrm{1}\mid\left({z}^{\mathrm{2}} +\mathrm{1}\right)+\left({y}^{\mathrm{2}} +\mathrm{1}\right)\mid{z}^{\mathrm{2}} −\mathrm{1}\mid\right)=\frac{\mathrm{15}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{zx}}\left(\mid{z}^{\mathrm{2}} −\mathrm{1}\mid\left({x}^{\mathrm{2}} +\mathrm{1}\right)+\left({z}^{\mathrm{2}} +\mathrm{1}\right)\mid{x}^{\mathrm{2}} −\mathrm{1}\mid\right)=\frac{\mathrm{63}}{\mathrm{4}} \\ $$$$...\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{4}\:\mathrm{solutions}\:\mathrm{as}\:\mathrm{I}\:\mathrm{got}\:\mathrm{before} \\ $$$$\mathrm{by}\:\mathrm{using}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{combinations}\:\mathrm{of} \\ $$$$\mid{t}^{\mathrm{2}} −\mathrm{1}\mid=\pm\left({t}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{8}\:\mathrm{solutions}\:\mathrm{but}\:\mathrm{only}\:\mathrm{4}\:\mathrm{fit}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{equations} \\ $$

Commented by mr W last updated on 16/Jul/19

great sir!

$${great}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com