
Question and Answers Forum
Question Number 64332 by Chi Mes Try last updated on 16/Jul/19
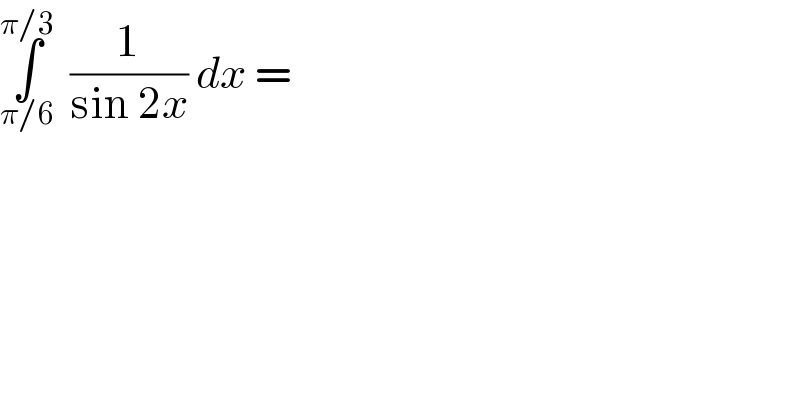
Commented by mathmax by abdo last updated on 16/Jul/19
![let A =∫_(π/6) ^(π/3) (dx/(sin(2x))) changement 2x=t give A =∫_(π/3) ^((2π)/3) (dt/(2sint)) =_(tan((t/2))=u) (1/2) ∫_(1/(√3)) ^(√3) ((2du)/((1+u^2 )((2u)/(1+u^2 )))) =(1/2) ∫_(1/(√3)) ^(√3) (du/u) =(1/2)[ln∣u∣]_(1/(√3)) ^(√3) =(1/2){ln((√3))+ln((√3))} =((ln(3))/2) A =((ln(3))/2) .](Q64344.png)
Commented by Tony Lin last updated on 17/Jul/19

| ||
Question and Answers Forum | ||
Question Number 64332 by Chi Mes Try last updated on 16/Jul/19 | ||
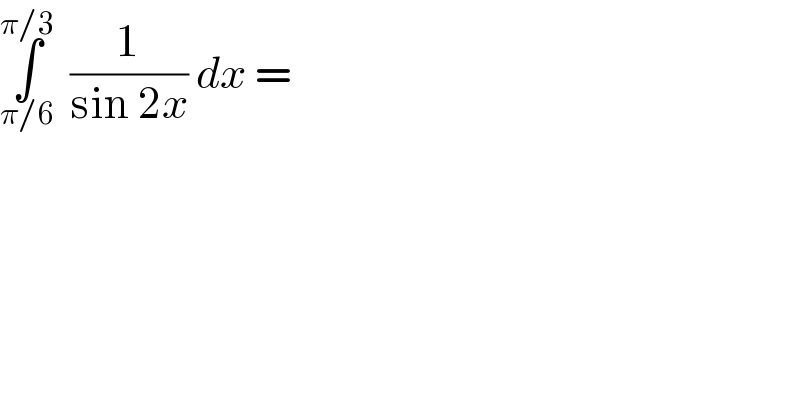 | ||
Commented by mathmax by abdo last updated on 16/Jul/19 | ||
![let A =∫_(π/6) ^(π/3) (dx/(sin(2x))) changement 2x=t give A =∫_(π/3) ^((2π)/3) (dt/(2sint)) =_(tan((t/2))=u) (1/2) ∫_(1/(√3)) ^(√3) ((2du)/((1+u^2 )((2u)/(1+u^2 )))) =(1/2) ∫_(1/(√3)) ^(√3) (du/u) =(1/2)[ln∣u∣]_(1/(√3)) ^(√3) =(1/2){ln((√3))+ln((√3))} =((ln(3))/2) A =((ln(3))/2) .](Q64344.png) | ||
Commented by Tony Lin last updated on 17/Jul/19 | ||
 | ||