I = ∫(dx/(sinx + sin2x))


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 6444 by sanusihammed last updated on 27/Jun/16

$I = \int \frac{d x}{s i n x + s i n 2 x}$
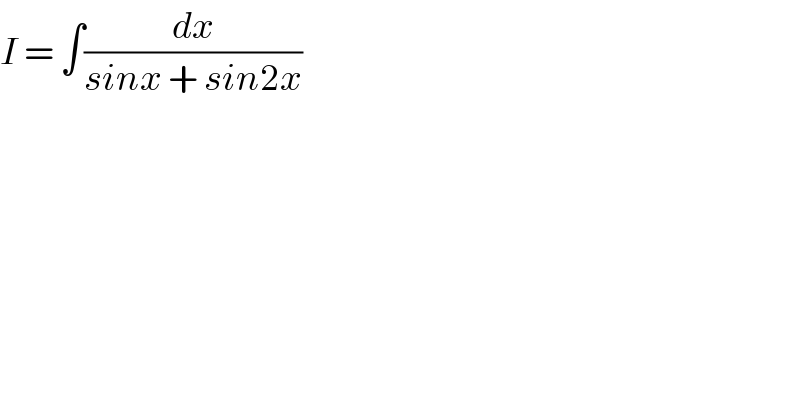
Commented by Temp last updated on 27/Jun/16

$Try www . WolframAlpha . com$ $search :$ $‘ ‘ i n t 1 / (s i n (x) + s i n (2 x)) {d x}^{″}$ $if you want, for example, \int_{1}^{2} x d x :$ $‘ ‘ i n t x d x f r o m x = 1 t o 2^{″}$
	Answered by Yozzii last updated on 27/Jun/16
	$I=∫(dx/(sinx+sin2x))=∫(dx/(sinx(1+2cosx))) Let u=tan0.5x⇒(2/(1+u^2 ))du=dx sinx=((2u)/(1+u^2 )) and cosx=((1−u^2 )/(1+u^2 )). ∴I=∫((2/(1+u^2 ))/(((2u)/(1+u^2 ))(1+((2(1−u^2 ))/(1+u^2 )))))du I=∫(((1+u^2 ))/(u(1+u^2 +2−2u^2 )))du I=∫((1+u^2 )/(u(3−u^2 )))du I=−∫((1+u^2 )/(u(u−(√3))(u+(√3))))du Let ((1+u^2 )/(u(u−(√3))(u+(√3))))≡(a/u)+(b/(u−(√3)))+(c/(u+(√3))) ≡((a(u^2 −3)+bu(u+(√3))+cu(u−(√3)))/(u(u+(√3))(u−(√3)))) ∴1+u^2 =a(u^2 −3)+bu(u+(√3))+cu(u−(√3)) Let u=0∴ 1=a(−3)⇒a=((−1)/3). Let u=(√3)⇒4=b(√3)(2(√3)) 4=6b⇒b=(2/3) Let u=−(√3)⇒4=c(−(√3))(−2(√3)) c=(2/3). ∴ I=−∫{(2/3)((1/(u+(√3)))+(1/(u−(√3))))−(1/(3u))}du I=−(1/3)∫{2((1/(u+(√3)))+(1/(u−(√3))))−(1/u)}du I=((−1)/3)[2ln∣(u+(√3))(u−(√3))∣−ln∣u∣]+C I=((−1)/3)ln∣(((u^2 −3)^2 )/u)∣+C I=(1/3)ln∣(u/((u^2 −3)^2 ))∣+C I=(1/3)ln∣((tan0.5x)/((tan^2 0.5x−3)^2 ))∣+C$
	$I = \int \frac{d x}{s i n x + s i n 2 x} = \int \frac{d x}{s i n x (1 + 2 c o s x)}$ $L e t u = t a n 0.5 x \Rightarrow \frac{2}{1 + u^{2}} d u = d x$ $s i n x = \frac{2 u}{1 + u^{2}} a n d c o s x = \frac{1 - u^{2}}{1 + u^{2}} .$ $∴ I = \int \frac{2 / (1 + u^{2})}{\frac{2 u}{1 + u^{2}} (1 + \frac{2 (1 - u^{2})}{1 + u^{2}})} d u$ $I = \int \frac{(1 + u^{2})}{u (1 + u^{2} + 2 - 2 u^{2})} d u$ $I = \int \frac{1 + u^{2}}{u (3 - u^{2})} d u$ $I = - \int \frac{1 + u^{2}}{u (u - \sqrt{3}) (u + \sqrt{3})} d u$ $L e t \frac{1 + u^{2}}{u (u - \sqrt{3}) (u + \sqrt{3})} \equiv \frac{a}{u} + \frac{b}{u - \sqrt{3}} + \frac{c}{u + \sqrt{3}}$ $\equiv \frac{a (u^{2} - 3) + b u (u + \sqrt{3}) + c u (u - \sqrt{3})}{u (u + \sqrt{3}) (u - \sqrt{3})}$ $∴ 1 + u^{2} = a (u^{2} - 3) + b u (u + \sqrt{3}) + c u (u - \sqrt{3})$ $L e t u = 0 ∴ 1 = a (- 3) \Rightarrow a = \frac{- 1}{3} .$ $L e t u = \sqrt{3} \Rightarrow 4 = b \sqrt{3} (2 \sqrt{3})$ $4 = 6 b \Rightarrow b = \frac{2}{3}$ $L e t u = - \sqrt{3} \Rightarrow 4 = c (- \sqrt{3}) (- 2 \sqrt{3})$ $c = \frac{2}{3} .$ $∴ I = - \int {\frac{2}{3} (\frac{1}{u + \sqrt{3}} + \frac{1}{u - \sqrt{3}}) - \frac{1}{3 u}} d u$ $I = - \frac{1}{3} \int {2 (\frac{1}{u + \sqrt{3}} + \frac{1}{u - \sqrt{3}}) - \frac{1}{u}} d u$ $I = \frac{- 1}{3} [2 l n ∣ (u + \sqrt{3}) (u - \sqrt{3}) ∣ - l n ∣ u ∣] + C$ $I = \frac{- 1}{3} l n ∣ \frac{{(u^{2} - 3)}^{2}}{u} ∣ + C$ $I = \frac{1}{3} l n ∣ \frac{u}{{(u^{2} - 3)}^{2}} ∣ + C$ $I = \frac{1}{3} l n ∣ \frac{t a n 0.5 x}{{({t a n}^{2} 0.5 x - 3)}^{2}} ∣ + C$
	Commented by nburiburu last updated on 27/Jun/16

	$t h e r e i s a n o t h e r w a y, i n s t e a d u n i v e r s a l t r i g o n o m e t r y s u b s t i t u t i o n :$ $\int \frac{1}{s i n x (1 + 2 c o s x)} . d x . \frac{s i n x}{s i n x} =$ $\int \frac{s i n x}{{s i n}^{2} x (1 + 2 c o s x)} . d x =$ $\int \frac{s i n x}{(1 - {c o s}^{2} x) (1 + 2 c o s x)} . d x$ $t = c o s x$ $d t = - s i n x d x$ $\int \frac{- 1}{(1 - t^{2}) (1 + 2 t)} . d t$ $a n d u s i n g r a t i o n a l d e s c o m p o s i t i o n i t i s s o l v e d .$ $1 - t^{2} = (1 - t) (1 + t)$ $= - \int \frac{A}{1 - t} d t - \int \frac{B}{1 + t} d t - \int \frac{C}{1 + 2 t} d t =$ $= A l n (1 - t) - B l n (1 + t) - \frac{C}{2} l n (1 + 2 t) + c$ $w h e r e$ $1 = A (1 + t) (1 + 2 t) + B (1 - t) (1 + 2 t) + C (1 - t^{2})$ $a n d i f t = 1 : 1 = A . 2.3 \Rightarrow A = \frac{1}{6}$ $i f t = - 1 : 1 = B (- 2) (- 1) \Rightarrow B = \frac{1}{2}$ $i f t = - \frac{1}{2} : 1 = C (1 - \frac{1}{4}) \Rightarrow C = \frac{4}{3}$ $s o$ $= \frac{1}{6} l n (1 - c o s x) - \frac{1}{2} l n (1 + c o s x) - \frac{2}{3} l n (1 + 2 c o s x) + c$
	Commented by sanusihammed last updated on 27/Jun/16

	$I r e a l l y a p p r e c i a t e$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum