
Question and Answers Forum
Question Number 64448 by mathmax by abdo last updated on 18/Jul/19
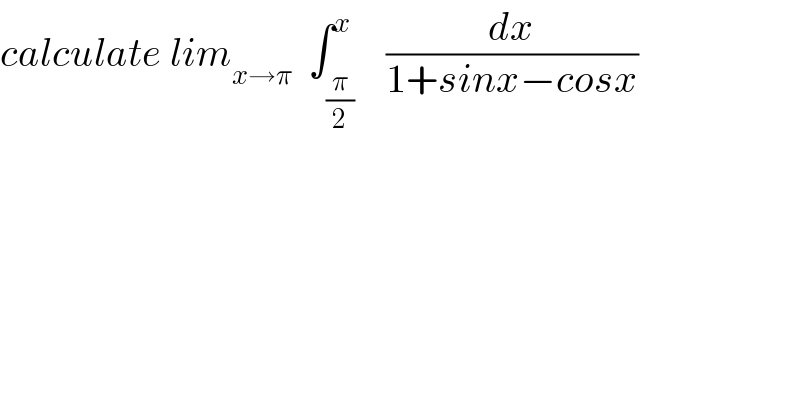
Commented by mathmax by abdo last updated on 19/Jul/19
![let A(x) =∫_(π/2) ^x (dt/(1+sint−cost)) changement tan((t/2))=u vive A(x) =∫_1 ^(tan((x/2))) ((2du)/((1+u^2 )(1+((2u)/(1+u^2 ))−((1−u^2 )/(1+u^2 ))))) =∫_1 ^(tan((x/2))) ((2du)/(1+u^2 +2u−1+u^2 )) =∫_1 ^(tan((x/2))) ((2du)/(2u^2 +2u)) =∫_1 ^(tan((x/2))) (du/(u(u+1))) =∫_1 ^(tan((x/2))) {(1/u)−(1/(u+1))}du =[ln∣(u/(u+1))∣]_1 ^(tan((x/2))) =ln∣((tan((x/2)))/(tan((x/2))+1))∣−ln((1/2)) ⇒lim_(x→π) A(x) =0+ln(2) =ln(2).](Q64567.png)
Answered by Tanmay chaudhury last updated on 18/Jul/19

| ||
Question and Answers Forum | ||
Question Number 64448 by mathmax by abdo last updated on 18/Jul/19 | ||
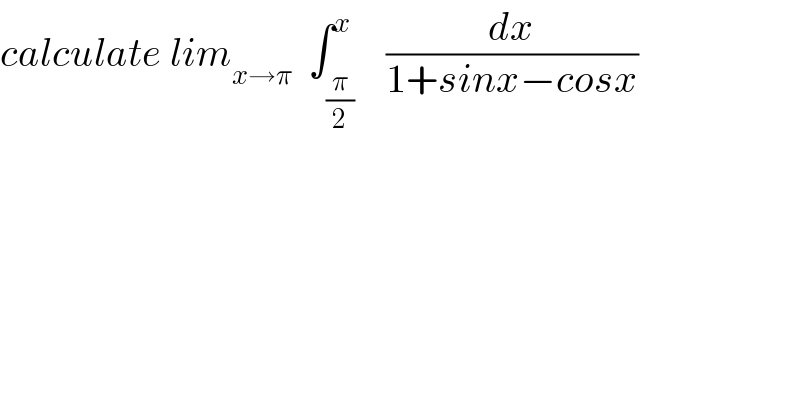 | ||
Commented by mathmax by abdo last updated on 19/Jul/19 | ||
![let A(x) =∫_(π/2) ^x (dt/(1+sint−cost)) changement tan((t/2))=u vive A(x) =∫_1 ^(tan((x/2))) ((2du)/((1+u^2 )(1+((2u)/(1+u^2 ))−((1−u^2 )/(1+u^2 ))))) =∫_1 ^(tan((x/2))) ((2du)/(1+u^2 +2u−1+u^2 )) =∫_1 ^(tan((x/2))) ((2du)/(2u^2 +2u)) =∫_1 ^(tan((x/2))) (du/(u(u+1))) =∫_1 ^(tan((x/2))) {(1/u)−(1/(u+1))}du =[ln∣(u/(u+1))∣]_1 ^(tan((x/2))) =ln∣((tan((x/2)))/(tan((x/2))+1))∣−ln((1/2)) ⇒lim_(x→π) A(x) =0+ln(2) =ln(2).](Q64567.png) | ||
Answered by Tanmay chaudhury last updated on 18/Jul/19 | ||
 | ||
| ||