Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 64640 by Tawa1 last updated on 19/Jul/19

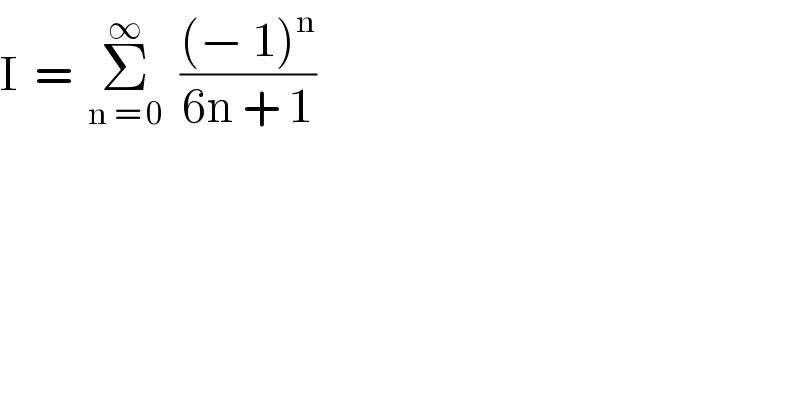
I = Σ_(n = 0) ^∞ (((− 1)^n )/(6n + 1))

$$\mathrm{I}\:\:=\:\:\underset{\mathrm{n}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}\:\:\frac{\left(−\:\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{6n}\:+\:\mathrm{1}} \\ $$

Commented by mathmax by abdo last updated on 20/Jul/19

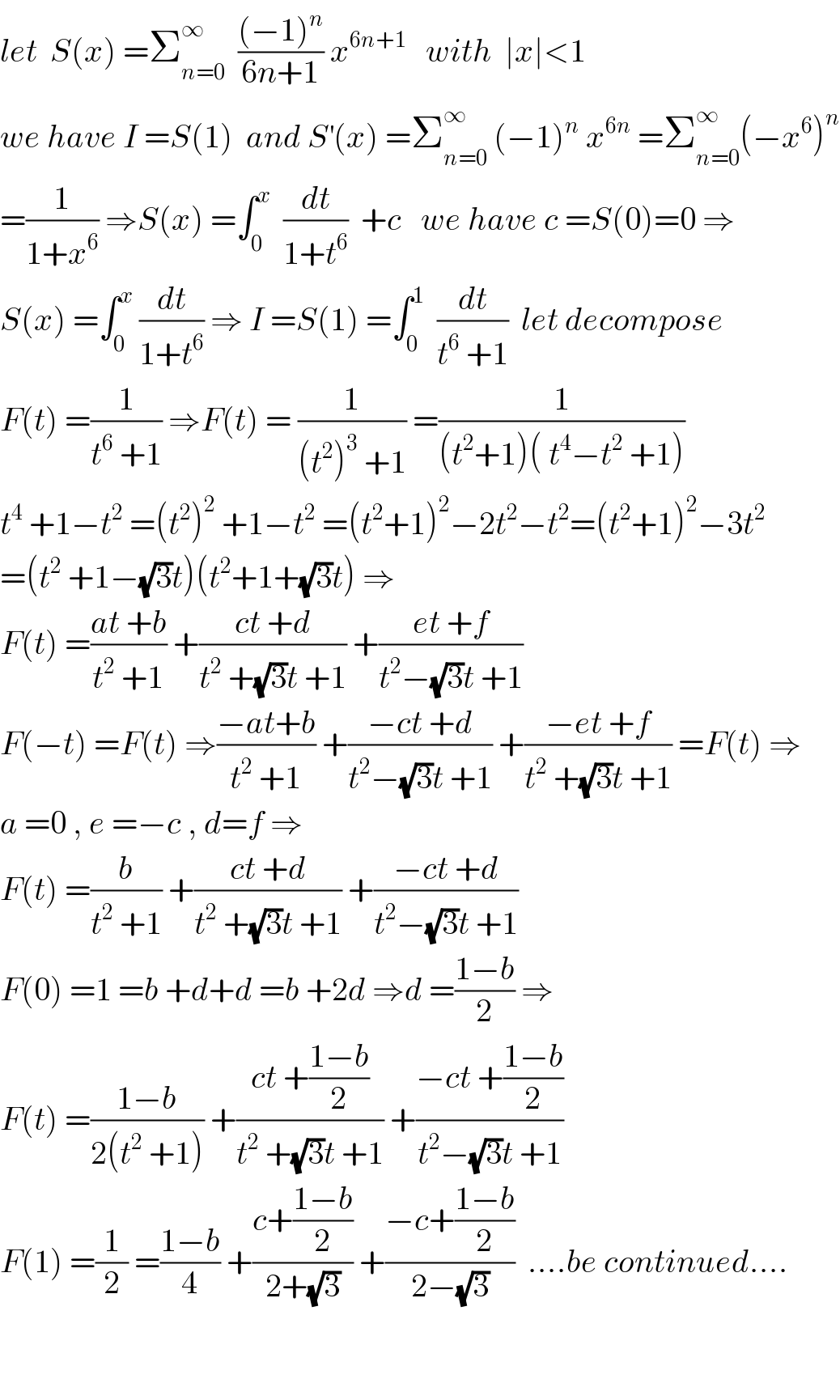
let S(x) =Σ_(n=0) ^∞ (((−1)^n )/(6n+1)) x^(6n+1) with ∣x∣<1 we have I =S(1) and S^′ (x) =Σ_(n=0) ^∞ (−1)^n x^(6n) =Σ_(n=0) ^∞ (−x^6 )^n =(1/(1+x^6 )) ⇒S(x) =∫_0 ^x (dt/(1+t^6 )) +c we have c =S(0)=0 ⇒ S(x) =∫_0 ^x (dt/(1+t^6 )) ⇒ I =S(1) =∫_0 ^1 (dt/(t^6 +1)) let decompose F(t) =(1/(t^6 +1)) ⇒F(t) = (1/((t^2 )^3 +1)) =(1/((t^2 +1)( t^4 −t^2 +1))) t^4 +1−t^2 =(t^2 )^2 +1−t^2 =(t^2 +1)^2 −2t^2 −t^2 =(t^2 +1)^2 −3t^2 =(t^2 +1−(√3)t)(t^2 +1+(√3)t) ⇒ F(t) =((at +b)/(t^2 +1)) +((ct +d)/(t^2 +(√3)t +1)) +((et +f)/(t^2 −(√3)t +1)) F(−t) =F(t) ⇒((−at+b)/(t^2 +1)) +((−ct +d)/(t^2 −(√3)t +1)) +((−et +f)/(t^2 +(√3)t +1)) =F(t) ⇒ a =0 , e =−c , d=f ⇒ F(t) =(b/(t^2 +1)) +((ct +d)/(t^2 +(√3)t +1)) +((−ct +d)/(t^2 −(√3)t +1)) F(0) =1 =b +d+d =b +2d ⇒d =((1−b)/2) ⇒ F(t) =((1−b)/(2(t^2 +1))) +((ct +((1−b)/2))/(t^2 +(√3)t +1)) +((−ct +((1−b)/2))/(t^2 −(√3)t +1)) F(1) =(1/2) =((1−b)/4) +((c+((1−b)/2))/(2+(√3))) +((−c+((1−b)/2))/(2−(√3))) ....be continued....

$${let}\:\:{S}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{6}{n}+\mathrm{1}}\:{x}^{\mathrm{6}{n}+\mathrm{1}} \:\:\:{with}\:\:\mid{x}\mid<\mathrm{1} \\ $$$${we}\:{have}\:{I}\:={S}\left(\mathrm{1}\right)\:\:{and}\:{S}^{'} \left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{6}{n}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−{x}^{\mathrm{6}} \right)^{{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{6}} }\:\Rightarrow{S}\left({x}\right)\:=\int_{\mathrm{0}} ^{{x}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{6}} }\:\:+{c}\:\:\:{we}\:{have}\:{c}\:={S}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow \\ $$$${S}\left({x}\right)\:=\int_{\mathrm{0}} ^{{x}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{6}} }\:\Rightarrow\:{I}\:={S}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{{t}^{\mathrm{6}} \:+\mathrm{1}}\:\:{let}\:{decompose} \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{1}}{{t}^{\mathrm{6}} \:+\mathrm{1}}\:\Rightarrow{F}\left({t}\right)\:=\:\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} \right)^{\mathrm{3}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left(\:{t}^{\mathrm{4}} −{t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${t}^{\mathrm{4}} \:+\mathrm{1}−{t}^{\mathrm{2}} \:=\left({t}^{\mathrm{2}} \right)^{\mathrm{2}} \:+\mathrm{1}−{t}^{\mathrm{2}} \:=\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{t}^{\mathrm{2}} −{t}^{\mathrm{2}} =\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3}{t}^{\mathrm{2}} \\ $$$$=\left({t}^{\mathrm{2}} \:+\mathrm{1}−\sqrt{\mathrm{3}}{t}\right)\left({t}^{\mathrm{2}} +\mathrm{1}+\sqrt{\mathrm{3}}{t}\right)\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{{at}\:+{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{t}\:+\mathrm{1}}\:+\frac{{et}\:+{f}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{3}}{t}\:+\mathrm{1}} \\ $$$${F}\left(−{t}\right)\:={F}\left({t}\right)\:\Rightarrow\frac{−{at}+{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−{ct}\:+{d}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{3}}{t}\:+\mathrm{1}}\:+\frac{−{et}\:+{f}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{t}\:+\mathrm{1}}\:={F}\left({t}\right)\:\Rightarrow \\ $$$${a}\:=\mathrm{0}\:,\:{e}\:=−{c}\:,\:{d}={f}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{t}\:+\mathrm{1}}\:+\frac{−{ct}\:+{d}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{3}}{t}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{1}\:={b}\:+{d}+{d}\:={b}\:+\mathrm{2}{d}\:\Rightarrow{d}\:=\frac{\mathrm{1}−{b}}{\mathrm{2}}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{1}−{b}}{\mathrm{2}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\frac{{ct}\:+\frac{\mathrm{1}−{b}}{\mathrm{2}}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{t}\:+\mathrm{1}}\:+\frac{−{ct}\:+\frac{\mathrm{1}−{b}}{\mathrm{2}}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{3}}{t}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{1}−{b}}{\mathrm{4}}\:+\frac{{c}+\frac{\mathrm{1}−{b}}{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{3}}}\:+\frac{−{c}+\frac{\mathrm{1}−{b}}{\mathrm{2}}}{\mathrm{2}−\sqrt{\mathrm{3}}}\:\:....{be}\:{continued}.... \\ $$$$ \\ $$$$ \\ $$

Commented by Tawa1 last updated on 20/Jul/19

God bless you sir. I will be waiting

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{be}\:\mathrm{waiting} \\ $$

Commented by mathmax by abdo last updated on 20/Jul/19

you are welcome.

$${you}\:{are}\:{welcome}. \\ $$

Answered by mr W last updated on 20/Jul/19

let S(x)=Σ_(n=0) ^∞ (((−1)^n x^(6n+1) )/(6n+1)) I=S(1) S′(x)=Σ_(n=0) ^∞ (−1)^n x^(6n) S′(x)=Σ_(n=0) ^∞ (−x^6 )^n =(1/(1+x^6 )) ⇒S(x)=∫(dx/(1+x^6 ))=(1/(4(√3))) ln ((x^2 +(√3)x+1)/(x^2 −(√3)x+1))+(1/6)[tan^(−1) (2x+(√3))+tan^(−1) (2x−(√3))]+(1/3)tan^(−1) x+C ⇒S(0)=C=0 ⇒S(x)=(1/(4(√3))) ln ((x^2 +(√3)x+1)/(x^2 −(√3)x+1))+(1/6)[tan^(−1) (2x+(√3))+tan^(−1) (2x−(√3))]+(1/3)tan^(−1) x ⇒I=S(1)=(1/(4(√3))) ln ((2+(√3))/(2−(√3)))+(1/6)[tan^(−1) (2+(√3))+tan^(−1) (2−(√3))]+(1/3)tan^(−1) 1 =(1/(2(√3))) ln (2+(√3))+(1/6)×(π/2)+(π/3)×(π/4) ⇒I=(1/6)[π+(√3) ln (2+(√3))]

$${let}\:{S}\left({x}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{6}{n}+\mathrm{1}} }{\mathrm{6}{n}+\mathrm{1}} \\ $$$${I}={S}\left(\mathrm{1}\right) \\ $$$${S}'\left({x}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{6}{n}} \\ $$$${S}'\left({x}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−{x}^{\mathrm{6}} \right)^{{n}} =\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{6}} } \\ $$$$\Rightarrow{S}\left({x}\right)=\int\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{6}} }=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\:\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)\right]+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} {x}+{C} \\ $$$$\Rightarrow{S}\left(\mathrm{0}\right)={C}=\mathrm{0} \\ $$$$\Rightarrow{S}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\:\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)\right]+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} {x} \\ $$$$\Rightarrow{I}={S}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\:\mathrm{ln}\:\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}−\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}+\sqrt{\mathrm{3}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\right]+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \mathrm{1} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{6}}×\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{3}}×\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow{I}=\frac{\mathrm{1}}{\mathrm{6}}\left[\pi+\sqrt{\mathrm{3}}\:\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\right] \\ $$

Commented by mathmax by abdo last updated on 21/Jul/19

thank you sir mrv.

$${thank}\:{you}\:{sir}\:{mrv}. \\ $$

Commented by mathmax by abdo last updated on 21/Jul/19

the important result here is that ∫ (dx/(1+x^6 )) =(1/(4(√3)))ln(((x^2 +(√3)x+1)/(x^2 −(√3)x+1)))+(1/6){ arctan(2x+(√3))+arctan(2x−(√3))}+(1/3)arctanx +c

$${the}\:{important}\:{result}\:{here}\:{is}\:{that} \\ $$$$\int\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{6}} }\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}{ln}\left(\frac{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}\right)+\frac{\mathrm{1}}{\mathrm{6}}\left\{\:{arctan}\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)+{arctan}\left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)\right\}+\frac{\mathrm{1}}{\mathrm{3}}{arctanx}\:+{c} \\ $$

Commented by mr W last updated on 21/Jul/19

thanks sir! can you confirm the result?

$${thanks}\:{sir}! \\ $$$${can}\:{you}\:{confirm}\:{the}\:{result}? \\ $$

Commented by Tawa1 last updated on 21/Jul/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mathmax by abdo last updated on 21/Jul/19

its correct sir the same result is given by integral calculator application its correct.

$${its}\:{correct}\:{sir}\:{the}\:{same}\:{result}\:{is}\:{given}\:{by}\:{integral}\:{calculator} \\ $$$${application}\:{its}\:{correct}. \\ $$

Commented by Cmr 237 last updated on 27/Aug/19

please can you prove that S(x)=Σ_(k=0) ^n (−x^6 )^k =(1/(1+x^6 )) please

$$\mathrm{please}\:\mathrm{can}\:\mathrm{you}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{S}\left(\mathrm{x}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\left(−\mathrm{x}^{\mathrm{6}} \right)^{\mathrm{k}} =\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{6}} } \\ $$$$\mathrm{please} \\ $$

Commented by mathmax by abdo last updated on 27/Aug/19

this equality is true if we know that ∣x∣<1 proof (1/(1+x^6 )) =(1/(1−(−x^6 ))) =Σ_(n=0) ^∞ (−x^6 )^n =Σ_(n=0) ^∞ (−1)^n x^(6n)

$${this}\:{equality}\:{is}\:{true}\:{if}\:\:{we}\:{know}\:{that}\:\mid{x}\mid<\mathrm{1} \\ $$$${proof}\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{6}} }\:=\frac{\mathrm{1}}{\mathrm{1}−\left(−{x}^{\mathrm{6}} \right)}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−{x}^{\mathrm{6}} \right)^{{n}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{6}{n}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com