Question Number 64709 by ajfour last updated on 20/Jul/19
Commented by ajfour last updated on 20/Jul/19
$${If}\:{regions}\:{A}\:{and}\:{B}\:{have}\:{the}\:{same} \\ $$$${area},\:{and}\:{both}\:{parabolas}\:{have} \\ $$$${the}\:{same}\:{shape}\:{but}\:{their}\:{axis}\:\bot\:{to} \\ $$$${each}\:{other},\:{then}\:{determine} \\ $$$${the}\:{equation}\:{of}\:{the}\:{red}\:{parabola}. \\ $$
Answered by mr W last updated on 22/Jul/19
![say both touch at point P(−h,h^2 ) y=x^2 (dy/dx)=2x eqn. of red parabola: x=−s+(y−t)^2 ⇒y=t±(√(x+s)) (dx/dy)=2(y−t) ⇒(dy/dx)=(1/(2(y−t))) at point P: −h=−s+(h^2 −t)^2 m=−2h=(1/(2(h^2 −t))) ⇒t=h^2 +(1/(4h)) ⇒s=h+(1/(16h^2 )) intersection of parabolas: x=−s+(x^2 −t)^2 ⇒x^4 −2tx^2 −x+t^2 −s=0 ⇒x^4 −(2h^2 +(1/(2h)))x^2 −x+(h^4 −(h/2))=0 (x+h)^2 (x^2 +qx+r)=0 (x^2 +2hx+h^2 )(x^2 +qx+r)=0 x^4 +(2h+q)x^3 +(h^2 +r+2hq)x^2 +(h^2 q+2hr)x+h^2 r=0 ⇒2h+q=0⇒q=−2h ⇒h^2 +r+2hq=−2h^2 −(1/(2h)) ⇒h^2 q+2hr=−1 ⇒h^2 r=h^4 −(h/2)⇒r=h^2 −(1/(2h)) h^2 +r+2hq=h^2 +h^2 −(1/(2h))−4h^2 =−2h^2 −(1/(2h))⇒ok h^2 q+2hr=−2h^3 +2h(h^2 −(1/(2h)))=−1⇒ok ⇒x^2 −2hx+h^2 −(1/(2h))=0 ⇒x=h±(√(h^2 −(h^2 −(1/(2h)))))=h±(1/(√(2h))) A=∫_(−h) ^(h−(1/(√(2h)))) [t−(√(x+s))−x^2 ]dx =[tx−(2/3)(x+s)^(3/2) −(1/3)x^3 ]_(−h) ^(h−(1/(√(2h)))) =(h^2 +(1/(4h)))(2h−(1/(√(2h))))−(2/3)(h−(1/(√(2h)))+h+(1/(16h^2 )))^(3/2) +(2/3)(−h+h+(1/(16h^2 )))^(3/2) −(1/3)(h−(1/(√(2h))))^3 −(1/3)h^3 =(h^2 +(1/(4h)))(2h−(1/(√(2h))))−(2/3)(2h−(1/(√(2h)))+(1/(16h^2 )))^(3/2) +(2/3)((1/(16h^2 )))^(3/2) −(1/3)(h−(1/(√(2h))))^3 −(1/3)h^3 A+B=∫_(−h) ^(h+(1/(√(2h)))) [t+(√(x+s))−x^2 ]dx+∫_(−s) ^(−h) 2(√(x+s))dx =[tx+(2/3)(x+s)^(3/2) −(1/3)x^3 ]_(−h) ^(h+(1/(√(2h)))) +(4/3)[(x+s)^(3/2) ]_(−s) ^(−h) =(h^2 +(1/(4h)))(2h+(1/(√(2h))))+(2/3)(h+(1/(√(2h)))+h+(1/(16h^2 )))^(3/2) −(2/3)(−h+h+(1/(16h^2 )))^(3/2) −(1/3)(h+(1/(√(2h))))^3 −(1/3)h^3 +(4/3)((1/(16h^2 )))^(3/2) =(h^2 +(1/(4h)))(2h+(1/(√(2h))))+(2/3)(2h+(1/(√(2h)))+(1/(16h^2 )))^(3/2) −(2/3)((1/(16h^2 )))^(3/2) −(1/3)(h+(1/(√(2h))))^3 −(1/3)h^3 +(4/3)((1/(16h^2 )))^(3/2) A+B=2A (h^2 +(1/(4h)))(2h+(1/(√(2h))))+(2/3)(2h+(1/(√(2h)))+(1/(16h^2 )))^(3/2) −(2/3)((1/(16h^2 )))^(3/2) −(1/3)(h+(1/(√(2h))))^3 −(1/3)h^3 +(4/3)((1/(16h^2 )))^(3/2) =2(h^2 +(1/(4h)))(2h−(1/(√(2h))))−(4/3)(2h−(1/(√(2h)))+(1/(16h^2 )))^(3/2) +(4/3)((1/(16h^2 )))^(3/2) −(2/3)(h−(1/(√(2h))))^3 −(2/3)h^3 ⇒(h^2 +(1/(4h)))((3/(√(2h)))−2h)+(2/3)(2h+(1/(√(2h)))+(1/(16h^2 )))^(3/2) +(4/3)(2h−(1/(√(2h)))+(1/(16h^2 )))^(3/2) −(2/3)((1/(16h^2 )))^(3/2) −(1/3)(h+(1/(√(2h))))^3 +(2/3)(h−(1/(√(2h))))^3 +(1/3)h^3 =0 ⇒h=2.55781774 ⇒h^2 =6.542431 eqn. of red parabola: ⇒x=−h−(1/(16h^2 ))+(y−h^2 −(1/(4h)))^2 i.e. x=−2.5673708+(y−6.6401712)^2 or x=y^2 −13.280342y+41.524503](Q64738.png)
$${say}\:{both}\:{touch}\:{at}\:{point}\:{P}\left(−{h},{h}^{\mathrm{2}} \right) \\ $$$${y}={x}^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2}{x} \\ $$$${eqn}.\:{of}\:{red}\:{parabola}: \\ $$$${x}=−{s}+\left({y}−{t}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{y}={t}\pm\sqrt{{x}+{s}} \\ $$$$\frac{{dx}}{{dy}}=\mathrm{2}\left({y}−{t}\right)\:\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\mathrm{2}\left({y}−{t}\right)} \\ $$$$ \\ $$$${at}\:{point}\:{P}: \\ $$$$−{h}=−{s}+\left({h}^{\mathrm{2}} −{t}\right)^{\mathrm{2}} \\ $$$${m}=−\mathrm{2}{h}=\frac{\mathrm{1}}{\mathrm{2}\left({h}^{\mathrm{2}} −{t}\right)} \\ $$$$\Rightarrow{t}={h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{h}} \\ $$$$\Rightarrow{s}={h}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} } \\ $$$$ \\ $$$${intersection}\:{of}\:{parabolas}: \\ $$$${x}=−{s}+\left({x}^{\mathrm{2}} −{t}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{4}} −\mathrm{2}{tx}^{\mathrm{2}} −{x}+{t}^{\mathrm{2}} −{s}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{4}} −\left(\mathrm{2}{h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}{h}}\right){x}^{\mathrm{2}} −{x}+\left({h}^{\mathrm{4}} −\frac{{h}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\left({x}+{h}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +{qx}+{r}\right)=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{2}{hx}+{h}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{qx}+{r}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +\left(\mathrm{2}{h}+{q}\right){x}^{\mathrm{3}} +\left({h}^{\mathrm{2}} +{r}+\mathrm{2}{hq}\right){x}^{\mathrm{2}} +\left({h}^{\mathrm{2}} {q}+\mathrm{2}{hr}\right){x}+{h}^{\mathrm{2}} {r}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{h}+{q}=\mathrm{0}\Rightarrow{q}=−\mathrm{2}{h} \\ $$$$\Rightarrow{h}^{\mathrm{2}} +{r}+\mathrm{2}{hq}=−\mathrm{2}{h}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{h}} \\ $$$$\Rightarrow{h}^{\mathrm{2}} {q}+\mathrm{2}{hr}=−\mathrm{1} \\ $$$$\Rightarrow{h}^{\mathrm{2}} {r}={h}^{\mathrm{4}} −\frac{{h}}{\mathrm{2}}\Rightarrow{r}={h}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{h}} \\ $$$${h}^{\mathrm{2}} +{r}+\mathrm{2}{hq}={h}^{\mathrm{2}} +{h}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{h}}−\mathrm{4}{h}^{\mathrm{2}} =−\mathrm{2}{h}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{h}}\Rightarrow{ok}\: \\ $$$${h}^{\mathrm{2}} {q}+\mathrm{2}{hr}=−\mathrm{2}{h}^{\mathrm{3}} +\mathrm{2}{h}\left({h}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{h}}\right)=−\mathrm{1}\Rightarrow{ok} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{hx}+{h}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{h}}=\mathrm{0} \\ $$$$\Rightarrow{x}={h}\pm\sqrt{{h}^{\mathrm{2}} −\left({h}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{h}}\right)}={h}\pm\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}} \\ $$$$ \\ $$$${A}=\int_{−{h}} ^{{h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}} \left[{t}−\sqrt{{x}+{s}}−{x}^{\mathrm{2}} \right]{dx} \\ $$$$=\left[{tx}−\frac{\mathrm{2}}{\mathrm{3}}\left({x}+{s}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} \right]_{−{h}} ^{{h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}} \\ $$$$=\left({h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{h}}\right)\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)−\frac{\mathrm{2}}{\mathrm{3}}\left({h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+{h}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{2}}{\mathrm{3}}\left(−{h}+{h}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{3}}\left({h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{3}}{h}^{\mathrm{3}} \\ $$$$=\left({h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{h}}\right)\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{3}}\left({h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{3}}{h}^{\mathrm{3}} \\ $$$$ \\ $$$${A}+{B}=\int_{−{h}} ^{{h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}} \left[{t}+\sqrt{{x}+{s}}−{x}^{\mathrm{2}} \right]{dx}+\int_{−{s}} ^{−{h}} \mathrm{2}\sqrt{{x}+{s}}{dx} \\ $$$$=\left[{tx}+\frac{\mathrm{2}}{\mathrm{3}}\left({x}+{s}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} \right]_{−{h}} ^{{h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}} +\frac{\mathrm{4}}{\mathrm{3}}\left[\left({x}+{s}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{−{s}} ^{−{h}} \\ $$$$=\left({h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{h}}\right)\left(\mathrm{2}{h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)+\frac{\mathrm{2}}{\mathrm{3}}\left({h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+{h}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{2}}{\mathrm{3}}\left(−{h}+{h}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{3}}\left({h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{3}}{h}^{\mathrm{3}} +\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$=\left({h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{h}}\right)\left(\mathrm{2}{h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}{h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{3}}\left({h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{3}}{h}^{\mathrm{3}} +\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$ \\ $$$${A}+{B}=\mathrm{2}{A} \\ $$$$\left({h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{h}}\right)\left(\mathrm{2}{h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}{h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{3}}\left({h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{3}}{h}^{\mathrm{3}} +\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\mathrm{2}\left({h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{h}}\right)\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)−\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{2}}{\mathrm{3}}\left({h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)^{\mathrm{3}} −\frac{\mathrm{2}}{\mathrm{3}}{h}^{\mathrm{3}} \\ $$$$\Rightarrow\left({h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{h}}\right)\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}{h}}}−\mathrm{2}{h}\right)+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}{h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{3}}\left({h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)^{\mathrm{3}} +\frac{\mathrm{2}}{\mathrm{3}}\left({h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{3}}{h}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow{h}=\mathrm{2}.\mathrm{55781774}\:\Rightarrow{h}^{\mathrm{2}} =\mathrm{6}.\mathrm{542431} \\ $$$${eqn}.\:{of}\:{red}\:{parabola}: \\ $$$$\Rightarrow{x}=−{h}−\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }+\left({y}−{h}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}{h}}\right)^{\mathrm{2}} \\ $$$${i}.{e}.\:{x}=−\mathrm{2}.\mathrm{5673708}+\left({y}−\mathrm{6}.\mathrm{6401712}\right)^{\mathrm{2}} \\ $$$${or}\:{x}={y}^{\mathrm{2}} −\mathrm{13}.\mathrm{280342}{y}+\mathrm{41}.\mathrm{524503} \\ $$
Commented by MJS last updated on 21/Jul/19
$$\mathrm{the}\:\mathrm{method}\:\mathrm{is}\:\mathrm{good}\:\mathrm{but}\:\mathrm{I}\:\mathrm{think}\:\mathrm{there}'\mathrm{s}\:\mathrm{an} \\ $$$$\mathrm{error}\:\mathrm{somewhere}.\:\mathrm{the}\:\mathrm{equation}\:\mathrm{for}\:{h}\:\mathrm{seems} \\ $$$$\mathrm{to}\:\mathrm{have}\:\mathrm{no}\:\mathrm{solution} \\ $$
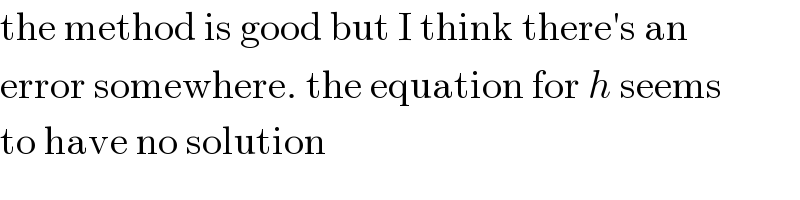
Commented by MJS last updated on 21/Jul/19
![I tried it similar but mirrored at y=x parabola 1: y^2 =x parabola 2: y=(x−p)^2 −q I put the tangential point as ((α),((−(√α))) ) this leads to (α)^(1/4) in some terms so I put α=β^4 I get these equations: parabola 1: y=±(√x) parabola 2: y=x^2 −((4β^6 +1)/(2β^2 ))x+((β^2 (2β^6 −1))/2) I get these points of interest: P_1 = (((β^4 −(√2)β+(1/(2β^2 )))),((β^2 −((√2)/(2β)))) ) [1^(st) intersection] P_2 = (((((4β^6 +1)/(4β^2 ))−((√(16β^6 +1))/(4β^2 )))),(0) ) [1^(st) zero] P_3 = ((β^4 ),((−β^2 )) ) [2^(nd) intersection] P_4 = (((((4β^6 +1)/(4β^2 ))+((√(16β^6 +1))/(4β^2 )))),(0) ) [2^(nd) zero] P_5 = (((β^4 +(√2)β+(1/(2β^2 )))),((β^2 +((√2)/(2β)))) ) [3^(rd) intersection] the equation of the integrals then leads to β^(12) −3(√2)β^9 +(3/4)β^6 −((3(√2))/8)β^3 +(1/(64))=0 [ignoring an absolute value ⇒ β≥(1/(2)^(1/6) )≈.890899 ⇒ α≥(1/(4)^(1/3) )≈.629961] β=(t)^(1/3) ; β≥(1/(2)^(1/6) )>0∧t≥(1/(√2))>0 t^4 −3(√2)t^3 +(3/4)t^2 −((3(√2))/8)t+(1/(64))=0 I solved this with my usual method putting (t−a−(√b))(t−a+(√b))(t−c−(√d))(t−c+(√d))=0 and got a=−1+((3(√2))/4) b=2−((3(√2))/2) c=1+((3(√2))/4) d=2+((3(√2))/2) t∈R∧t≥(1/(√2)) ⇒ t=1+((3(√2))/4)+((√(8+6(√2)))/2) ⇒ β=(t)^(1/3) ⇒ α=(t^4 )^(1/3) β=((1+((3(√2))/4)+((√(8+6(√2)))/2)))^(1/3) ≈1.59932 α=((((4481)/(64))+((99(√2))/2)+((3(65+46(√2))(√(4+3(√2))))/8)))^(1/3) ≈6.54243 parabola 2: y=x^2 −13.2803x+41.5245](Q64795.png)
$$\mathrm{I}\:\mathrm{tried}\:\mathrm{it}\:\mathrm{similar}\:\mathrm{but}\:\mathrm{mirrored}\:\mathrm{at}\:{y}={x} \\ $$$$\mathrm{parabola}\:\mathrm{1}:\:{y}^{\mathrm{2}} ={x} \\ $$$$\mathrm{parabola}\:\mathrm{2}:\:{y}=\left({x}−{p}\right)^{\mathrm{2}} −{q} \\ $$$$\mathrm{I}\:\mathrm{put}\:\mathrm{the}\:\mathrm{tangential}\:\mathrm{point}\:\mathrm{as}\:\begin{pmatrix}{\alpha}\\{−\sqrt{\alpha}}\end{pmatrix} \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\sqrt[{\mathrm{4}}]{\alpha}\:\mathrm{in}\:\mathrm{some}\:\mathrm{terms}\:\mathrm{so}\:\mathrm{I}\:\mathrm{put}\:\alpha=\beta^{\mathrm{4}} \\ $$$$\mathrm{I}\:\mathrm{get}\:\mathrm{these}\:\mathrm{equations}: \\ $$$$\mathrm{parabola}\:\mathrm{1}:\:{y}=\pm\sqrt{{x}} \\ $$$$\mathrm{parabola}\:\mathrm{2}:\:{y}={x}^{\mathrm{2}} −\frac{\mathrm{4}\beta^{\mathrm{6}} +\mathrm{1}}{\mathrm{2}\beta^{\mathrm{2}} }{x}+\frac{\beta^{\mathrm{2}} \left(\mathrm{2}\beta^{\mathrm{6}} −\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{I}\:\mathrm{get}\:\mathrm{these}\:\mathrm{points}\:\mathrm{of}\:\mathrm{interest}: \\ $$$${P}_{\mathrm{1}} =\begin{pmatrix}{\beta^{\mathrm{4}} −\sqrt{\mathrm{2}}\beta+\frac{\mathrm{1}}{\mathrm{2}\beta^{\mathrm{2}} }}\\{\beta^{\mathrm{2}} −\frac{\sqrt{\mathrm{2}}}{\mathrm{2}\beta}}\end{pmatrix}\:\:\left[\mathrm{1}^{\mathrm{st}} \:\mathrm{intersection}\right] \\ $$$${P}_{\mathrm{2}} =\begin{pmatrix}{\frac{\mathrm{4}\beta^{\mathrm{6}} +\mathrm{1}}{\mathrm{4}\beta^{\mathrm{2}} }−\frac{\sqrt{\mathrm{16}\beta^{\mathrm{6}} +\mathrm{1}}}{\mathrm{4}\beta^{\mathrm{2}} }}\\{\mathrm{0}}\end{pmatrix}\:\:\left[\mathrm{1}^{\mathrm{st}} \:\mathrm{zero}\right] \\ $$$${P}_{\mathrm{3}} =\begin{pmatrix}{\beta^{\mathrm{4}} }\\{−\beta^{\mathrm{2}} }\end{pmatrix}\:\:\left[\mathrm{2}^{\mathrm{nd}} \:\mathrm{intersection}\right] \\ $$$${P}_{\mathrm{4}} =\begin{pmatrix}{\frac{\mathrm{4}\beta^{\mathrm{6}} +\mathrm{1}}{\mathrm{4}\beta^{\mathrm{2}} }+\frac{\sqrt{\mathrm{16}\beta^{\mathrm{6}} +\mathrm{1}}}{\mathrm{4}\beta^{\mathrm{2}} }}\\{\mathrm{0}}\end{pmatrix}\:\:\left[\mathrm{2}^{\mathrm{nd}} \:\mathrm{zero}\right] \\ $$$${P}_{\mathrm{5}} =\begin{pmatrix}{\beta^{\mathrm{4}} +\sqrt{\mathrm{2}}\beta+\frac{\mathrm{1}}{\mathrm{2}\beta^{\mathrm{2}} }}\\{\beta^{\mathrm{2}} +\frac{\sqrt{\mathrm{2}}}{\mathrm{2}\beta}}\end{pmatrix}\:\:\left[\mathrm{3}^{\mathrm{rd}} \:\mathrm{intersection}\right] \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{integrals}\:\mathrm{then}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\beta^{\mathrm{12}} −\mathrm{3}\sqrt{\mathrm{2}}\beta^{\mathrm{9}} +\frac{\mathrm{3}}{\mathrm{4}}\beta^{\mathrm{6}} −\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{8}}\beta^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{64}}=\mathrm{0} \\ $$$$\left[\mathrm{ignoring}\:\mathrm{an}\:\mathrm{absolute}\:\mathrm{value}\:\Rightarrow\:\beta\geqslant\frac{\mathrm{1}}{\sqrt[{\mathrm{6}}]{\mathrm{2}}}\approx.\mathrm{890899}\:\Rightarrow\:\alpha\geqslant\frac{\mathrm{1}}{\sqrt[{\mathrm{3}}]{\mathrm{4}}}\approx.\mathrm{629961}\right] \\ $$$$\beta=\sqrt[{\mathrm{3}}]{{t}};\:\beta\geqslant\frac{\mathrm{1}}{\sqrt[{\mathrm{6}}]{\mathrm{2}}}>\mathrm{0}\wedge{t}\geqslant\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}>\mathrm{0} \\ $$$${t}^{\mathrm{4}} −\mathrm{3}\sqrt{\mathrm{2}}{t}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{4}}{t}^{\mathrm{2}} −\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{8}}{t}+\frac{\mathrm{1}}{\mathrm{64}}=\mathrm{0} \\ $$$$\mathrm{I}\:\mathrm{solved}\:\mathrm{this}\:\mathrm{with}\:\mathrm{my}\:\mathrm{usual}\:\mathrm{method}\:\mathrm{putting} \\ $$$$\left({t}−{a}−\sqrt{{b}}\right)\left({t}−{a}+\sqrt{{b}}\right)\left({t}−{c}−\sqrt{{d}}\right)\left({t}−{c}+\sqrt{{d}}\right)=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{got} \\ $$$${a}=−\mathrm{1}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}\:\:{b}=\mathrm{2}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:{c}=\mathrm{1}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}\:\:{d}=\mathrm{2}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${t}\in\mathbb{R}\wedge{t}\geqslant\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\Rightarrow\:{t}=\mathrm{1}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}+\frac{\sqrt{\mathrm{8}+\mathrm{6}\sqrt{\mathrm{2}}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\beta=\sqrt[{\mathrm{3}}]{{t}}\:\Rightarrow\:\alpha=\sqrt[{\mathrm{3}}]{{t}^{\mathrm{4}} } \\ $$$$\beta=\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}+\frac{\sqrt{\mathrm{8}+\mathrm{6}\sqrt{\mathrm{2}}}}{\mathrm{2}}}\approx\mathrm{1}.\mathrm{59932} \\ $$$$\alpha=\sqrt[{\mathrm{3}}]{\frac{\mathrm{4481}}{\mathrm{64}}+\frac{\mathrm{99}\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\mathrm{3}\left(\mathrm{65}+\mathrm{46}\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{4}+\mathrm{3}\sqrt{\mathrm{2}}}}{\mathrm{8}}}\approx\mathrm{6}.\mathrm{54243} \\ $$$$\mathrm{parabola}\:\mathrm{2}:\:{y}={x}^{\mathrm{2}} −\mathrm{13}.\mathrm{2803}{x}+\mathrm{41}.\mathrm{5245} \\ $$
Commented by mr W last updated on 22/Jul/19
$${thank}\:{you}\:{for}\:{checking}\:{and}\:{for}\:{the} \\ $$$${great}\:{solution}\:{sir}! \\ $$$${i}\:{had}\:{a}\:{mistake}\:{in}\:{the}\:{final}\:{equation}. \\ $$$${now}\:{it}\:{should}\:{be}\:{correct}.\:{our}\:{solutions} \\ $$$${are}\:{the}\:{same}\:{now}.\:{i}\:{got} \\ $$$${h}^{\mathrm{2}} =\mathrm{6}.\mathrm{542431} \\ $$$${h}^{\mathrm{2}} \:{is}\:\alpha\:{in}\:{your}\:{working}. \\ $$
Commented by MJS last updated on 22/Jul/19
![(h^2 +(1/(4h)))((3/(√(2h)))−2h)+(2/3)(2h+(1/(√(2h)))+(1/(16h^2 )))^(3/2) +(4/3)(2h−(1/(√(2h)))+(1/(16h^2 )))^(3/2) −(2/3)((1/(16h^2 )))^(3/2) −(1/3)(h+(1/(√(2h))))^3 +(2/3)(h−(1/(√(2h))))^3 +(1/3)h^3 =0 we know h>0 2h+(1/(√(2h)))+(1/(16h^2 ))=(((4(√2)h(√h)+1)/(4h)))^2 2h−(1/(√(2h)))+(1/(16h^2 ))=(((4(√2)h(√h)−1)/(4h)))^2 [believing 4(√2)h(√h)−1>0 ⇒ h>((2)^(1/3) /4)≈.314980] ⇒ the equation can be transformed to −((64h^6 −192(√2)h^(9/2) +48h^3 −24(√2)h^(3/2) +1)/(48h^3 ))=0 h^6 −3(√2)h^(9/2) +(3/4)h^3 −((3(√2))/8)h^(3/2) +(1/(64))=0 h=β^2 [β>0] β^(12) −3(√2)β^9 +(3/4)β^6 −((3(√2))/8)β^3 +(1/(64))=0 ... it′s the same as my solution](Q64839.png)
$$\left({h}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{h}}\right)\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}{h}}}−\mathrm{2}{h}\right)+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}{h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{2}{h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{3}}\left({h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)^{\mathrm{3}} +\frac{\mathrm{2}}{\mathrm{3}}\left({h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}\right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{3}}{h}^{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{know}\:{h}>\mathrm{0} \\ $$$$\mathrm{2}{h}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }=\left(\frac{\mathrm{4}\sqrt{\mathrm{2}}{h}\sqrt{{h}}+\mathrm{1}}{\mathrm{4}{h}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{h}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}{h}}}+\frac{\mathrm{1}}{\mathrm{16}{h}^{\mathrm{2}} }=\left(\frac{\mathrm{4}\sqrt{\mathrm{2}}{h}\sqrt{{h}}−\mathrm{1}}{\mathrm{4}{h}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\left[\mathrm{believing}\:\mathrm{4}\sqrt{\mathrm{2}}{h}\sqrt{{h}}−\mathrm{1}>\mathrm{0}\:\Rightarrow\:{h}>\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{4}}\approx.\mathrm{314980}\right] \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{equation}\:\mathrm{can}\:\mathrm{be}\:\mathrm{transformed}\:\mathrm{to} \\ $$$$−\frac{\mathrm{64}{h}^{\mathrm{6}} −\mathrm{192}\sqrt{\mathrm{2}}{h}^{\frac{\mathrm{9}}{\mathrm{2}}} +\mathrm{48}{h}^{\mathrm{3}} −\mathrm{24}\sqrt{\mathrm{2}}{h}^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{1}}{\mathrm{48}{h}^{\mathrm{3}} }=\mathrm{0} \\ $$$${h}^{\mathrm{6}} −\mathrm{3}\sqrt{\mathrm{2}}{h}^{\frac{\mathrm{9}}{\mathrm{2}}} +\frac{\mathrm{3}}{\mathrm{4}}{h}^{\mathrm{3}} −\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{8}}{h}^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{1}}{\mathrm{64}}=\mathrm{0} \\ $$$${h}=\beta^{\mathrm{2}} \:\left[\beta>\mathrm{0}\right] \\ $$$$\beta^{\mathrm{12}} −\mathrm{3}\sqrt{\mathrm{2}}\beta^{\mathrm{9}} +\frac{\mathrm{3}}{\mathrm{4}}\beta^{\mathrm{6}} −\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{8}}\beta^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{64}}=\mathrm{0} \\ $$$$... \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{my}\:\mathrm{solution} \\ $$
Commented by mr W last updated on 22/Jul/19
$${ajfour}\:{sir}: \\ $$$${you}\:{are}\:{absolutely}\:{right}!\:{good} \\ $$$${observation}!\:{i}\:{lost}\:{a}\:{tiny}\:{part}\:{in}\:{the} \\ $$$${area}\:{B}\:{indeed}. \\ $$$${i}\:{have}\:{fixed}\:{the}\:{result}. \\ $$
Commented by ajfour last updated on 22/Jul/19
$${Thank}\:{you}\:{Sir},\:{but}\:{MjS}\:{Sir}'{s} \\ $$$${answer}\:{is}\:{perfect}.\:{we}\:{wont}\:{know} \\ $$$${how}\:{to}\:{get}\:{the}\:{answer}\:{in}\:{radical} \\ $$$${form},\:{from}\:{our}\:{eq}.\:{in}\:{h}. \\ $$
Commented by ajfour last updated on 22/Jul/19
$${I}\:{salute}\:{you}\:{sir}! \\ $$
Commented by mr W last updated on 22/Jul/19
$${the}\:{solution}\:{of}\:{MJS}\:{sir}\:{is}\:{indeed}\:{a} \\ $$$${perfect}\:{one}.\:{even}\:{though}\:{i}\:{knew}\:{that} \\ $$$${i}\:{could}\:{transfer}\:{my}\:{final}\:{equation}\:{for} \\ $$$${h}\:{into}\:{a}\:{polynomial}\:{one},\:{but}\:{due}\:{to} \\ $$$${the}\:{high}\:{power}\:{of}\:{the}\:{eqn}.\:{i}\:{gave}\:{up}. \\ $$$${because}\:{i}\:{wouldn}'{t}\:{be}\:{able}\:{to}\:{solve}\:{it}. \\ $$