Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 64735 by mmkkmm000m last updated on 20/Jul/19

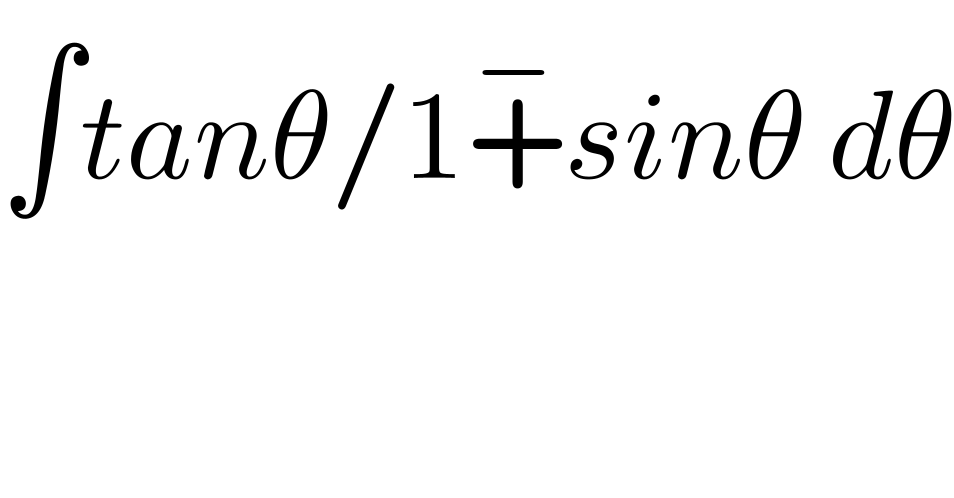
∫tanθ/1+^− sinθ dθ

$$\int{tan}\theta/\mathrm{1}\overset{−} {+}{sin}\theta\:{d}\theta \\ $$

Commented by mr W last updated on 21/Jul/19

dear sir: in Q64238 i asked if you could use a smaller font such that your posts become better readable for other people. it seems that you wouldn′t change this, what a pity! that′s ok, i don′t care. but i find it very unkind that you just ignore my kind request without any reply. i think, being polite to each other is the foundation of this forum, otherwise why should people help other people?

$${dear}\:{sir}: \\ $$$${in}\:{Q}\mathrm{64238}\:{i}\:{asked}\:{if}\:{you}\:{could}\:{use} \\ $$$${a}\:{smaller}\:{font}\:{such}\:{that}\:{your}\:{posts} \\ $$$${become}\:{better}\:{readable}\:{for}\:{other} \\ $$$${people}.\:{it}\:{seems}\:{that}\:{you}\:{wouldn}'{t} \\ $$$${change}\:{this},\:{what}\:{a}\:{pity}!\:{that}'{s}\:{ok}, \\ $$$${i}\:{don}'{t}\:{care}.\:{but}\:{i}\:{find}\:{it}\:{very}\:{unkind} \\ $$$${that}\:{you}\:{just}\:{ignore}\:{my}\:{kind}\:{request} \\ $$$${without}\:{any}\:{reply}.\:{i}\:{think},\:{being}\:{polite} \\ $$$${to}\:{each}\:{other}\:{is}\:{the}\:{foundation}\:{of} \\ $$$${this}\:{forum},\:{otherwise}\:{why}\:{should} \\ $$$${people}\:{help}\:{other}\:{people}? \\ $$

Commented by mathmax by abdo last updated on 21/Jul/19

let I =∫ ((tanθ)/(1+sinθ)) dθ changement tan((θ/2))=t give I =∫ (((2t)/(1−t^2 ))/(1+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) = ∫ ((4tdt)/((1−t^2 )(1+t^2 +2t))) =−∫ ((4t)/((t^2 −1)(t+1)^2 ))dt =−4∫ ((4t)/((t−1)(t+1)^3 ))dt let decompose F(t) =(t/((t−1)(t+1)^3 )) F(t) =(a/(t−1)) +(b/(t+1)) +(c/((t+1)^2 )) +(d/((t+1)^3 )) a =lim_(x→1) (t−1)F(t) =(1/8) d =lim_(t→−1) (t+1)^3 F(t) =(1/2) ⇒F(t) =(1/(8(t−1))) +(b/(t+1)) +(c/((t+1)^2 ))+(1/(2(t+1)^3 )) lim_(t→+∞) tF(t) =0 =a+b ⇒b =−(1/8) ⇒ F(t) =(1/(8(t−1))) −(1/(8(t+1))) +(c/((t+1)^2 )) +(1/(2(t+1)^3 )) F(0) =0 =−(1/8)−(1/8) +c +(1/2) =−(1/4)+(1/2) +c =(1/4) +c ⇒c =−(1/4) ⇒ F(t) =(1/(8(t−1))) −(1/(8(t+1)))−(1/(4(t+1)^2 )) +(1/(2(t+1)^3 )) ⇒ ∫ F(t)dt =(1/8)ln∣t−1∣−(1/8)ln∣t+1∣+(1/(4(t+1)))−(1/(4(t+1)^2 )) +C =(1/8)ln∣((t−1)/(t+1))∣ +(1/(4(t+1)))−(1/(4(t+1)^2 )) +C ⇒ I =−(1/2)ln∣((t−1)/(t+1))∣−(1/((t+1))) +(1/((t+1)^2 )) +C =−(1/2)ln∣((tan((θ/2))−1)/(tan((θ/2))+1))∣−(1/(1+tan((θ/2)))) +(1/((1+tan((θ/2)))^2 )) +C .

$${let}\:\:{I}\:=\int\:\:\frac{{tan}\theta}{\mathrm{1}+{sin}\theta}\:{d}\theta\:\:{changement}\:\:{tan}\left(\frac{\theta}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:=\int\:\:\frac{\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\int\:\:\frac{\mathrm{4}{tdt}}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \:+\mathrm{2}{t}\right)}\:=−\int\:\frac{\mathrm{4}{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=−\mathrm{4}\int\:\:\frac{\mathrm{4}{t}}{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)^{\mathrm{3}} }{dt}\:\:{let}\:{decompose}\:{F}\left({t}\right)\:=\frac{{t}}{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${F}\left({t}\right)\:=\frac{{a}}{{t}−\mathrm{1}}\:+\frac{{b}}{{t}+\mathrm{1}}\:+\frac{{c}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{d}}{\left({t}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{1}} \left({t}−\mathrm{1}\right){F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${d}\:={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right)^{\mathrm{3}} {F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{8}\left({t}−\mathrm{1}\right)}\:+\frac{{b}}{{t}+\mathrm{1}}\:+\frac{{c}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${lim}_{{t}\rightarrow+\infty} \:{tF}\left({t}\right)\:=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}\:=−\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{8}\left({t}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{8}\left({t}+\mathrm{1}\right)}\:+\frac{{c}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=−\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}}\:+{c}\:+\frac{\mathrm{1}}{\mathrm{2}}\:=−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\:+{c}\:=\frac{\mathrm{1}}{\mathrm{4}}\:+{c}\:\Rightarrow{c}\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{8}\left({t}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{8}\left({t}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{8}}{ln}\mid{t}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{8}}{ln}\mid{t}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:+{C}\:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid−\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:+{C} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{{tan}\left(\frac{\theta}{\mathrm{2}}\right)−\mathrm{1}}{{tan}\left(\frac{\theta}{\mathrm{2}}\right)+\mathrm{1}}\mid−\frac{\mathrm{1}}{\mathrm{1}+{tan}\left(\frac{\theta}{\mathrm{2}}\right)}\:+\frac{\mathrm{1}}{\left(\mathrm{1}+{tan}\left(\frac{\theta}{\mathrm{2}}\right)\right)^{\mathrm{2}} }\:+{C}\:. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com