Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 64829 by Tawa1 last updated on 22/Jul/19

Commented by Tawa1 last updated on 22/Jul/19

$$\mathrm{God}\mathrm{bless}\mathrm{you}\mathrm{sir}$$

Commented by Tony Lin last updated on 22/Jul/19

$$let\mathrm{\angle }BDC=\theta$$$$BC=\sqrt{{17}^2+{11}^2-2\times 17\times 11cos\theta }$$$$=\sqrt{410-374cos\theta }$$$$AB=\sqrt{{17}^2+{31}^2-2\times 17\times 31cos(\pi -\theta )}$$$$=\sqrt{{17}^2+{31}^2+2\times 17\times 31cos\theta }$$$$=\sqrt{1250+1054cos\theta }$$$$areaof△ABC$$$$=BC\times AB\times \frac{1}{2}$$$$=\frac{1}{2}\times (BD\times DC\times sin\theta +BD\times AD\times sin(\pi -\theta )$$$$=\frac{1}{2}\times 17\times (11+31)sin\theta$$$$=357sin\theta$$$$\Rightarrow \sqrt{(410-374cos\theta )(1250+1054cos\theta )}$$$$=714sin\theta$$$$\Rightarrow \sqrt{512500-35360cos\theta -394196{cos}^2\theta }$$$$=714sin\theta$$$$letcos\theta =t$$$$\Rightarrow \sqrt{512500-35360t-394196t^2}$$$$=714\sqrt{1-t^2}$$$$\Rightarrow 512500-35360t-394196t^2$$$$=509796-509796t^2$$$$\Rightarrow 115600t^2-35360t+2704=0$$$$\Rightarrow t=\frac{13}{85}$$$$areaof△BDC$$$$=\frac{1}{2}\times BD\times DC\times sin\theta$$$$=\frac{1}{2}\times 17\times 11\times \sqrt{1-{\left(\frac{13}{85}\right)}^2}$$$$=92.4$$

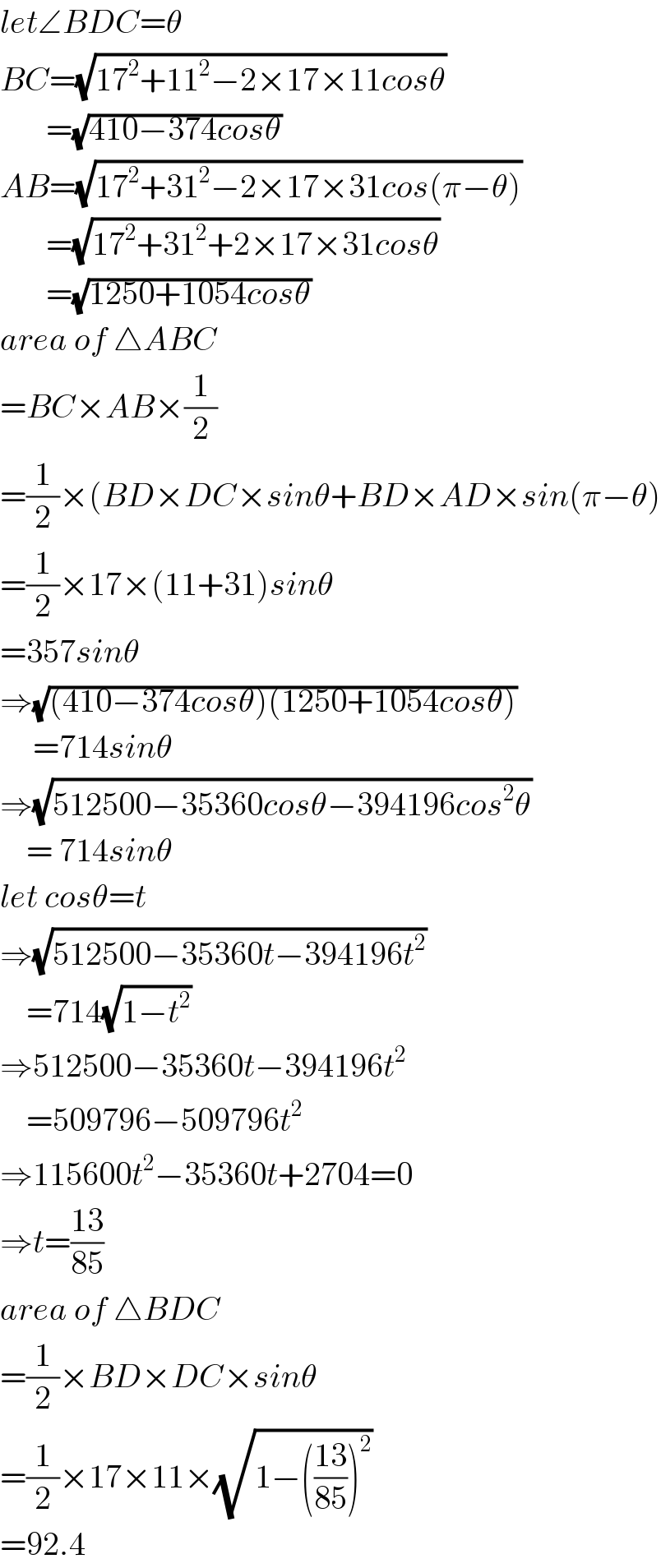
Commented by mathmax by abdo last updated on 23/Jul/19

$$whereareyoufromsirtony...$$

Commented by Tony Lin last updated on 23/Jul/19

$$Taiwan$$

Answered by MJS last updated on 22/Jul/19

$$\mathrm{put}\frac{A+C}{2}\mathrm{in}\mathrm{the}\mathrm{center}$$$$\Rightarrow A=\left(\begin{array}{c}-21\\ 0\end{array}\right)\mathrm{C}=\left(\begin{array}{c}21\\ 0\end{array}\right)D=\left(\begin{array}{c}10\\ 0\end{array}\right)$$$$B\mathrm{lies}\mathrm{on}\mathrm{the}\mathrm{circumcircle}{x}^2+y^2={21}^2$$$$B=\left(\begin{array}{c}x\\ \sqrt{441-x^2}\end{array}\right)$$$$\mid BD\mid =17$$$$\sqrt{{(x-10)}^2+{(\sqrt{441-x^2}-0)}^2}=17$$$$\sqrt{541-20x}=17$$$$x=\frac{63}{5}$$$$B=\left(\begin{array}{c}\frac{63}{5}\\ \frac{84}{5}\end{array}\right)$$$$\mid BC\mid =\sqrt{{(\frac{63}{5}-21)}^2+{(\frac{84}{5}-0)}^2}=\frac{42\sqrt{5}}{5}$$$$\Rightarrow \mathrm{the}\mathrm{shaded}\mathrm{triangle}\mathrm{has}\mathrm{sides}$$$$11,17,\frac{42\sqrt{5}}{5}$$$$\mathrm{the}\mathrm{area}\mathrm{of}\mathrm{a}\mathrm{triangle}\mathrm{with}\mathrm{sides}a,b,c\mathrm{is}$$$$\frac{\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}{4}$$$$\Rightarrow \mathrm{shaded}\mathrm{area}=\frac{462}{5}=92.4$$$$$$

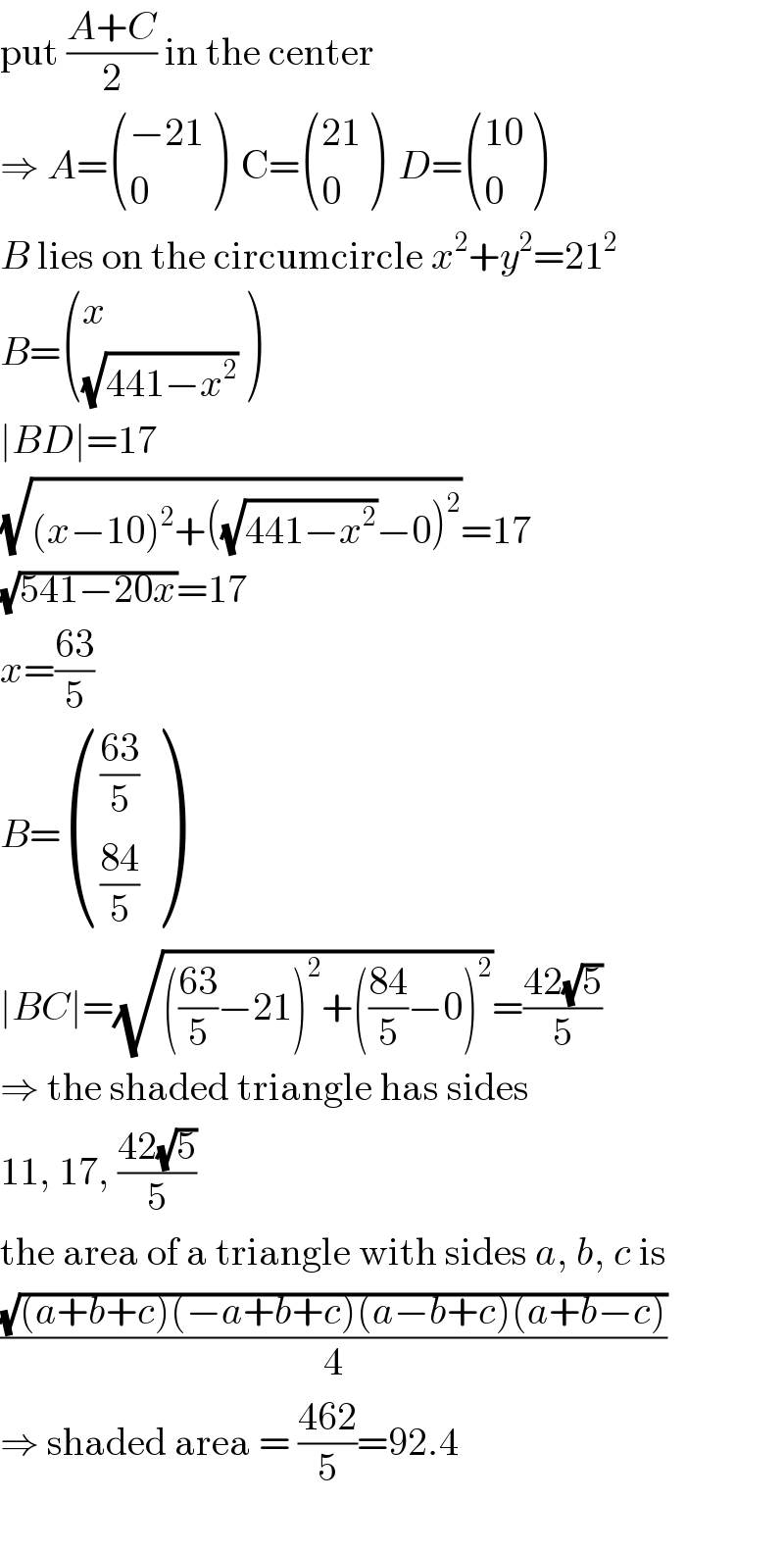
Commented by Tawa1 last updated on 22/Jul/19

$$\mathrm{God}\mathrm{bless}\mathrm{you}\mathrm{sir}$$

Answered by ajfour last updated on 22/Jul/19

Commented by ajfour last updated on 22/Jul/19

$$\cos \theta =\frac{{21}^2-{10}^2-{17}^2}{2\times 10\times 17}=\frac{13}{85}$$$$\sin \theta =\frac{\sqrt{7225-169}}{85}=\frac{84}{85}$$$$A_{rea}=\frac{1}{2}\times 11\times 17\sin \theta$$$$A_{rea}=\frac{11\times 17\times 84}{2\times 85}=\frac{11\times 42}{5}=\frac{462}{5}$$$$A_{rea}=92.4squnits◼$$

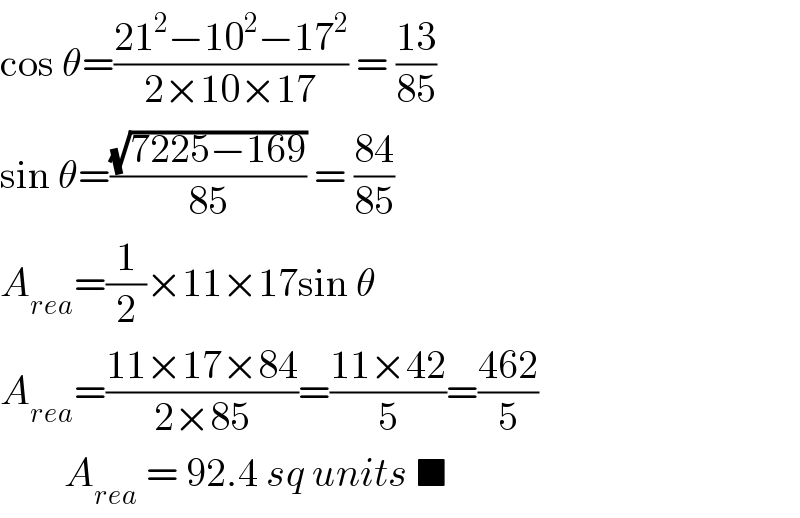
Commented by ajfour last updated on 22/Jul/19

$$soyoudontseemtolikethis$$$$solution,Tawa.$$

Commented by MJS last updated on 22/Jul/19

$${\mathrm{she}}^{\prime }\mathrm{s}\mathrm{not}\mathrm{yet}\mathrm{through}\mathrm{with}\mathrm{it}$$

Commented by Tawa1 last updated on 22/Jul/19

$$\mathrm{God}\mathrm{bless}\mathrm{you}\mathrm{sir}$$

Commented by Tawa1 last updated on 22/Jul/19

$$\mathrm{Hahaha}.\mathrm{No}\mathrm{sir},\mathrm{i}\mathrm{am}\mathrm{going}\mathrm{through}\mathrm{it}.$$

Commented by Tawa1 last updated on 22/Jul/19

$$\mathrm{And}\mathrm{i}\mathrm{am}\mathrm{grateful}\mathrm{sir}.\mathrm{God}\mathrm{bless}\mathrm{you}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com