
Question Number 64860 by Tawa1 last updated on 22/Jul/19

Commented by Tawa1 last updated on 22/Jul/19

$$\mathrm{Number}\:\mathrm{11}\:\mathrm{and}\:\mathrm{13} \\ $$
Commented by mathmax by abdo last updated on 22/Jul/19

$$\left.\mathrm{1}\right)\:{xy}^{''} \:+\left(\mathrm{2}{v}+\mathrm{1}\right){y}^{'} \:+{xy}\:=\mathrm{0}\:\:{let}\:{use}\:{the}\:{changement}\:{y}\:={x}^{−{v}} {z} \\ $$$$\Rightarrow{y}\:={e}^{−{vlnx}} {z}\:\Rightarrow{y}^{'} \:=−\frac{{v}}{{x}}\:{e}^{−{vlnx}} {z}\:+{e}^{−{vlnx}} {z}^{'} \\ $$$$=\left(−\frac{{v}}{{x}}\:{z}\:+{z}^{'} \right){e}^{−{vlnx}} \:\Rightarrow{y}^{''} \:=\left(\frac{{v}}{{x}^{\mathrm{2}} }{z}\:−\frac{{v}}{{x}}{z}'\:+{z}^{''} \right){e}^{−{vlnx}} \\ $$$$−\frac{{v}}{{x}}\:{e}^{−{vlnx}} \left(−\frac{{v}}{{x}}{z}\:+{z}^{'} \right)\:=\left(\frac{{v}}{{x}^{\mathrm{2}} }{z}−\frac{{v}}{{x}}{z}^{'} \:+{z}^{''} +\frac{{v}^{\mathrm{2}} }{{x}^{\mathrm{2}} }{z}−\frac{{v}}{{x}}{z}^{'} \right){e}^{−{vlnx}} \\ $$$$\left({e}\right)\Rightarrow\left(\frac{{v}}{{x}}{z}−{vz}^{'} \:+{xz}''\:+\frac{{v}}{{x}}{z}−{vz}^{'} \right){e}^{−{vlnx}} \:+\left(\mathrm{2}{v}+\mathrm{1}\right)\left(−\frac{{v}}{{x}}{z}\:+{z}^{'} \right){e}^{−{vlnx}} \\ $$$$+{xz}\:{e}^{−{vlnx}} \:=\mathrm{0}\:\Rightarrow \\ $$$$\frac{\mathrm{2}{v}}{{x}}{z}−\mathrm{2}{vz}^{'} \:+{xz}^{''} \:−\frac{\mathrm{2}{v}^{\mathrm{2}} }{{x}}{z}+\mathrm{2}{vz}^{'} −\frac{{v}}{{x}}{z}\:+{z}^{'} \:+{xz}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{2}{vz}\:−\mathrm{2}{vxz}^{'} \:+{x}^{\mathrm{2}} {z}^{''} \:−\mathrm{2}{v}^{\mathrm{2}} {z}\:+\mathrm{2}{vxz}^{'} −{vz}\:+{xz}^{'} \:+{x}^{\mathrm{2}} {z}\:=\mathrm{0}\:\Rightarrow \\ $$$${x}^{\mathrm{2}} {z}^{''} \:\:+\left(−\mathrm{2}{vx}\:+\mathrm{2}{vx}\:\:+{x}\right){z}^{'} \:+\left(\mathrm{2}{v}−{v}\:+{x}^{\mathrm{2}} \right){z}\:=\mathrm{0}\:\Rightarrow \\ $$$${x}^{\mathrm{2}} {z}^{''} \:+{xz}^{'} \:\:+\left({x}^{\mathrm{2}} \:+{v}\right){z}\:=\mathrm{0}\:\:\:{linear}\:\left({e}\right){at}\:\mathrm{2}^{{me}} \:{ordre}\:...{be}\:{continued}.... \\ $$
Commented by Tawa1 last updated on 22/Jul/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{waiting}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 24/Jul/19
$$\mathrm{Please}\:\mathrm{sir},\:\mathrm{the}\:\mathrm{rest}\:\mathrm{solution} \\ $$
Commented by mathmax by abdo last updated on 25/Jul/19
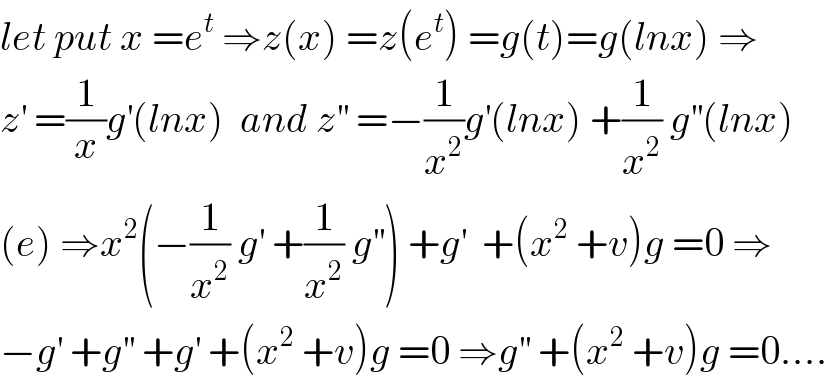
$${let}\:{put}\:{x}\:={e}^{{t}} \:\Rightarrow{z}\left({x}\right)\:={z}\left({e}^{{t}} \right)\:={g}\left({t}\right)={g}\left({lnx}\right)\:\Rightarrow \\ $$$${z}^{'} \:=\frac{\mathrm{1}}{{x}}{g}^{'} \left({lnx}\right)\:\:{and}\:{z}^{''} \:=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{g}^{'} \left({lnx}\right)\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{g}^{''} \left({lnx}\right) \\ $$$$\left({e}\right)\:\Rightarrow{x}^{\mathrm{2}} \left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{g}^{'} \:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{g}^{''} \right)\:+{g}^{'} \:\:+\left({x}^{\mathrm{2}} \:+{v}\right){g}\:=\mathrm{0}\:\Rightarrow \\ $$$$−{g}^{'} \:+{g}^{''} \:+{g}^{'} \:+\left({x}^{\mathrm{2}} \:+{v}\right){g}\:=\mathrm{0}\:\Rightarrow{g}^{''} \:+\left({x}^{\mathrm{2}} \:+{v}\right){g}\:=\mathrm{0}.... \\ $$
Commented by Tawa1 last updated on 25/Jul/19
$$\mathrm{Sir},\:\mathrm{the}\:\mathrm{final}\:\mathrm{answer}\:\mathrm{for}\:\mathrm{number}\:\mathrm{1}\:\:??? \\ $$
