Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 6491 by Temp last updated on 29/Jun/16

Is it possible such that two trancendental numbers add or multiply to give a whole number?

$$\mathrm{Is}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{such}\:\mathrm{that}\:\mathrm{two}\:\mathrm{trancendental} \\ $$$$\mathrm{numbers}\:\mathrm{add}\:\mathrm{or}\:\mathrm{multiply}\:\mathrm{to}\:\mathrm{give}\:\mathrm{a}\:\mathrm{whole}\:\mathrm{number}? \\ $$

Commented by prakash jain last updated on 29/Jun/16

π is transcendental. (1/π) is also transcendental. π×(1/π)=1

$$\pi\:\mathrm{is}\:\mathrm{transcendental}. \\ $$$$\frac{\mathrm{1}}{\pi}\:\mathrm{is}\:\mathrm{also}\:\mathrm{transcendental}. \\ $$$$\pi×\frac{\mathrm{1}}{\pi}=\mathrm{1} \\ $$

Commented by Temp last updated on 29/Jun/16

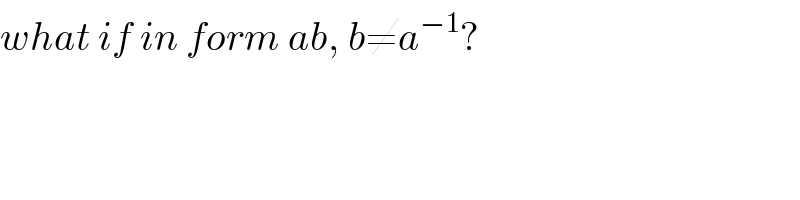
what if in form ab, b≠a^(−1) ?

$${what}\:{if}\:{in}\:{form}\:{ab},\:{b}\neq{a}^{−\mathrm{1}} ? \\ $$

Commented by Rasheed Soomro last updated on 29/Jun/16

π×(2/π)=2, where (2/π)≠π^(-1)

$$\pi×\frac{\mathrm{2}}{\pi}=\mathrm{2},\:{where}\:\frac{\mathrm{2}}{\pi}\neq\pi^{-\mathrm{1}} \\ $$

Commented by Temp last updated on 29/Jun/16

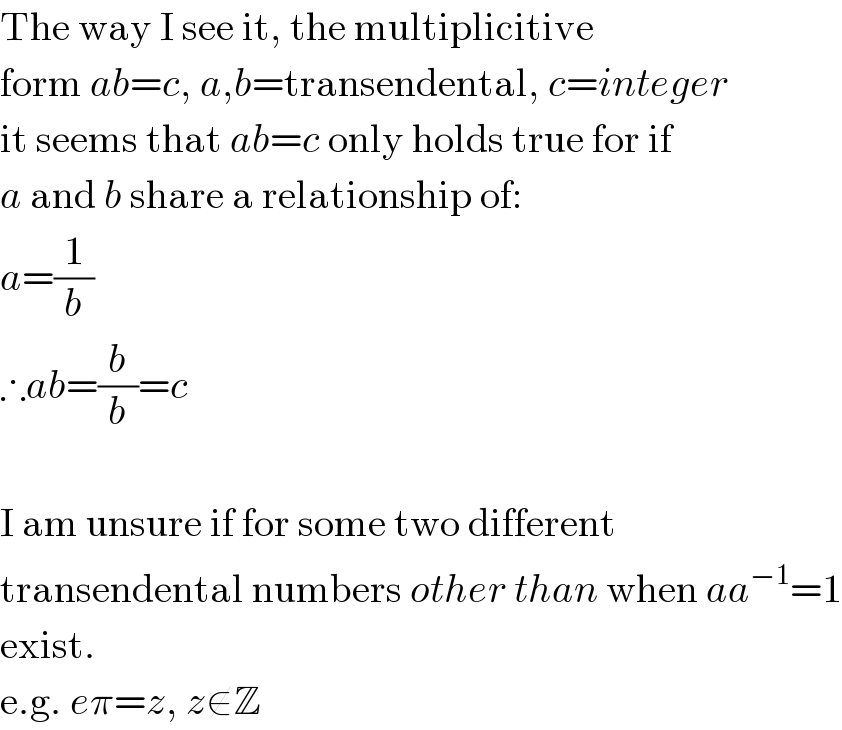
The way I see it, the multiplicitive form ab=c, a,b=transendental, c=integer it seems that ab=c only holds true for if a and b share a relationship of: a=(1/b) ∴ab=(b/b)=c I am unsure if for some two different transendental numbers other than when aa^(−1) =1 exist. e.g. eπ=z, z∉Z

$$\mathrm{The}\:\mathrm{way}\:\mathrm{I}\:\mathrm{see}\:\mathrm{it},\:\mathrm{the}\:\mathrm{multiplicitive} \\ $$$$\mathrm{form}\:{ab}={c},\:{a},{b}=\mathrm{transendental},\:{c}={integer} \\ $$$$\mathrm{it}\:\mathrm{seems}\:\mathrm{that}\:{ab}={c}\:\mathrm{only}\:\mathrm{holds}\:\mathrm{true}\:\mathrm{for}\:\mathrm{if} \\ $$$${a}\:\mathrm{and}\:{b}\:\mathrm{share}\:\mathrm{a}\:\mathrm{relationship}\:\mathrm{of}: \\ $$$${a}=\frac{\mathrm{1}}{{b}} \\ $$$$\therefore{ab}=\frac{{b}}{{b}}={c} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{unsure}\:\mathrm{if}\:\mathrm{for}\:\mathrm{some}\:\mathrm{two}\:\mathrm{different} \\ $$$$\mathrm{transendental}\:\mathrm{numbers}\:{other}\:{than}\:\mathrm{when}\:{aa}^{−\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{exist}. \\ $$$$\mathrm{e}.\mathrm{g}.\:{e}\pi={z},\:{z}\notin\mathbb{Z} \\ $$

Commented by Temp last updated on 29/Jun/16

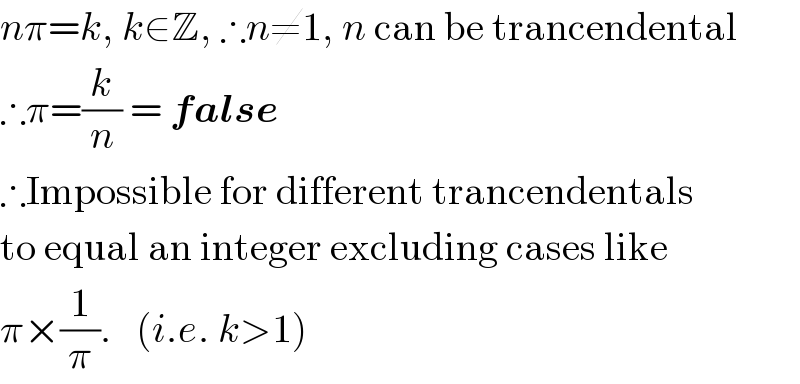
nπ=k, k∈Z, ∴n≠1, n can be trancendental ∴π=(k/n) = false ∴Impossible for different trancendentals to equal an integer excluding cases like π×(1/π). (i.e. k>1)

$${n}\pi={k},\:{k}\in\mathbb{Z},\:\therefore{n}\neq\mathrm{1},\:{n}\:\mathrm{can}\:\mathrm{be}\:\mathrm{trancendental} \\ $$$$\therefore\pi=\frac{{k}}{{n}}\:=\:\boldsymbol{{false}} \\ $$$$\therefore\mathrm{Impossible}\:\mathrm{for}\:\mathrm{different}\:\mathrm{trancendentals} \\ $$$$\mathrm{to}\:\mathrm{equal}\:\mathrm{an}\:\mathrm{integer}\:\mathrm{excluding}\:\mathrm{cases}\:\mathrm{like} \\ $$$$\pi×\frac{\mathrm{1}}{\pi}.\:\:\:\left({i}.{e}.\:{k}>\mathrm{1}\right) \\ $$

Commented by Rasheed Soomro last updated on 30/Jun/16

Say π,e and other transidental numbers, which can not be derived from one another by +,−,×,÷,power,root are said to be root-transedentals. π,−π,π^(−1) ,nπ,((mπ)/n)(m,n∈Z) are of same roots.e and π are root-transcidentals. Now what you want to say, can be said “Sum or product of two transidentals of different roots can′t be whole numbers” Am I right?

$${Say}\:\pi,{e}\:{and}\:{other}\:{transidental}\:{numbers}, \\ $$$${which}\:{can}\:{not}\:{be}\:{derived}\:{from}\:{one}\:{another} \\ $$$${by}\:+,−,×,\boldsymbol{\div},{power},{root}\:{are}\:{said}\:{to}\:{be}\:\boldsymbol{{root}}-\boldsymbol{{transedentals}}. \\ $$$$\:\pi,−\pi,\pi^{−\mathrm{1}} ,{n}\pi,\frac{{m}\pi}{{n}}\left({m},{n}\in\mathbb{Z}\right)\:{are} \\ $$$${of}\:{same}\:{roots}.\boldsymbol{{e}}\:{and}\:\pi\:{are}\:\:{root}-{transcidentals}. \\ $$$${Now}\:{what}\:{you}\:{want}\:{to}\:{say},\:{can}\:{be}\:{said}\: \\ $$$$``{Sum}\:{or}\:{product}\:{of}\:{two}\:{transidentals} \\ $$$${of}\:{different}\:{roots}\:{can}'{t}\:{be}\:{whole}\:{numbers}'' \\ $$$${Am}\:{I}\:{right}? \\ $$

Commented by prakash jain last updated on 29/Jun/16

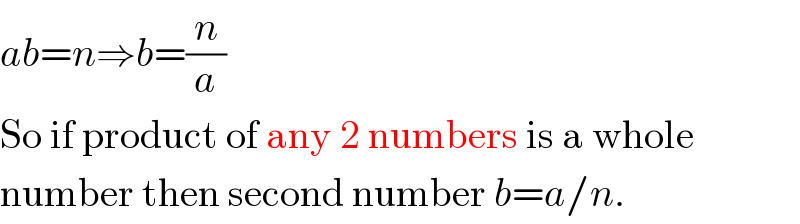
ab=n⇒b=(n/a) So if product of any 2 numbers is a whole number then second number b=a/n.

$${ab}={n}\Rightarrow{b}=\frac{{n}}{{a}} \\ $$$$\mathrm{So}\:\mathrm{if}\:\mathrm{product}\:\mathrm{of}\:\mathrm{any}\:\mathrm{2}\:\mathrm{numbers}\:\mathrm{is}\:\mathrm{a}\:\mathrm{whole} \\ $$$$\mathrm{number}\:\mathrm{then}\:\mathrm{second}\:\mathrm{number}\:{b}={a}/{n}. \\ $$

Answered by malwaan last updated on 02/Jul/16

e^(π(√(163))) is an integer e^(π(√(163))) = 262 537 412 640 768 744

$${e}^{\pi\sqrt{\mathrm{163}}} \:{is}\:{an}\:{integer} \\ $$$${e}^{\pi\sqrt{\mathrm{163}}} \:=\:\mathrm{262}\:\mathrm{537}\:\mathrm{412}\:\mathrm{640}\:\mathrm{768}\:\mathrm{744} \\ $$

Commented by malwaan last updated on 03/Jul/16

According to WolframAlpha e^(π(√(163))) =262537412640768743.99999999999925007.... what do you think? very small error because of calculation rounding

$${According}\:{to}\:{WolframAlpha} \\ $$$${e}^{\pi\sqrt{\mathrm{163}}} \:=\mathrm{262537412640768743}.\mathrm{99999999999925007}.... \\ $$$${what}\:{do}\:{you}\:{think}? \\ $$$${very}\:{small}\:{error}\:{because}\:{of}\:{calculation}\:{rounding} \\ $$

Commented by prakash jain last updated on 02/Jul/16

According to Wolfram alpha e^(π(√(163))) is a transcendental number. 2.6253..×10^(17)

$$\mathrm{According}\:\mathrm{to}\:\mathrm{Wolfram}\:\mathrm{alpha}\:{e}^{\pi\sqrt{\mathrm{163}}} \:\mathrm{is}\: \\ $$$$\mathrm{a}\:\mathrm{transcendental}\:\mathrm{number}. \\ $$$$\mathrm{2}.\mathrm{6253}..×\mathrm{10}^{\mathrm{17}} \\ $$

Commented by Rasheed Soomro last updated on 03/Jul/16

According to wikiepedia e^(π(√n)) is transcedental for any positive n

$${According}\:{to}\:{wikiepedia} \\ $$$${e}^{\pi\sqrt{{n}}} \:\:{is}\:{transcedental}\:{for}\:{any}\:{positive}\:{n} \\ $$

Commented by malwaan last updated on 03/Jul/16

e^(π(√(163))) had been conjectured around 1914 by the indian mathematician Srinivasa Ramanujan . In May 1974 John Brillo of the university of Arizona managed to prove that e^(π(√(163))) =262 537 412 640 768 744

$${e}^{\pi\sqrt{\mathrm{163}}} \:{had}\:{been}\:{conjectured}\:{around} \\ $$$$\mathrm{1914}\:{by}\:{the}\:{indian}\:{mathematician} \\ $$$${Srinivasa}\:{Ramanujan}\:. \\ $$$${In}\:{May}\:\mathrm{1974}\:{John}\:{Brillo}\:{of}\:{the} \\ $$$${university}\:{of}\:{Arizona}\:{managed}\:{to} \\ $$$${prove}\:{that} \\ $$$${e}^{\pi\sqrt{\mathrm{163}}} \:=\mathrm{262}\:\mathrm{537}\:\mathrm{412}\:\mathrm{640}\:\mathrm{768}\:\mathrm{744} \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 03/Jul/16

New knowledqe for me.

$${New}\:{knowledqe}\:{for}\:{me}. \\ $$

Commented by prakash jain last updated on 03/Jul/16

W. alpha clearly states that it is a trancendental number. It is almost an integer.

$$\mathrm{W}.\:\mathrm{alpha}\:\mathrm{clearly}\:\mathrm{states}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{a}\:\mathrm{trancendental} \\ $$$$\mathrm{number}. \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{almost}\:\mathrm{an}\:\mathrm{integer}. \\ $$

Commented by malwaan last updated on 04/Jul/16

I think you are right It is almost integer BUT my answer is from Crux Canadian mathematical Society. EUREKA NO. 4 June 1975

$${I}\:{think}\:{you}\:{are}\:{right} \\ $$$${It}\:{is}\:\boldsymbol{{almost}}\:{integer} \\ $$$$\boldsymbol{{BUT}}\:\:{my}\:{answer}\:{is}\:{from} \\ $$$$\boldsymbol{{Crux}} \\ $$$$\boldsymbol{{Canadian}}\:\boldsymbol{{mathematical}}\:\boldsymbol{{Society}}. \\ $$$$\boldsymbol{{EUREKA}}\:\boldsymbol{{NO}}.\:\mathrm{4}\:\boldsymbol{{June}}\:\mathrm{1975} \\ $$

Answered by Temp last updated on 01/Jul/16

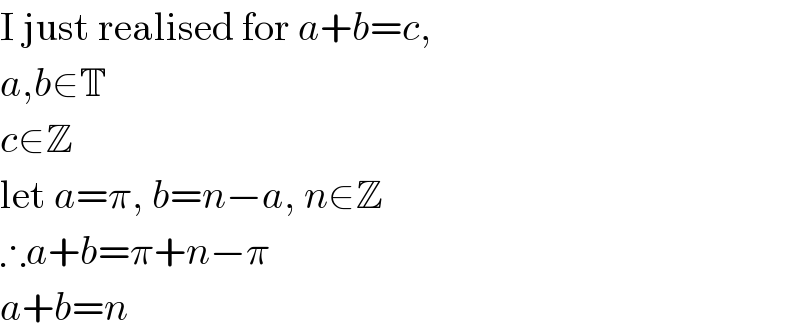
I just realised for a+b=c, a,b∈T c∈Z let a=π, b=n−a, n∈Z ∴a+b=π+n−π a+b=n

$$\mathrm{I}\:\mathrm{just}\:\mathrm{realised}\:\mathrm{for}\:{a}+{b}={c}, \\ $$$${a},{b}\in\mathbb{T} \\ $$$${c}\in\mathbb{Z} \\ $$$$\mathrm{let}\:{a}=\pi,\:{b}={n}−{a},\:{n}\in\mathbb{Z} \\ $$$$\therefore{a}+{b}=\pi+{n}−\pi \\ $$$${a}+{b}={n} \\ $$

Commented by Rasheed Soomro last updated on 01/Jul/16

π and n−π are derivations of same transcedental (π). Is there an example of two transcedentals which are not derivations of same transcedental and give the sum or product as whole number?

$$\pi\:{and}\:\:{n}−\pi\:{are}\:{derivations}\:{of}\:{same} \\ $$$${transcedental}\:\left(\pi\right). \\ $$$${Is}\:{there}\:{an}\:{example} \\ $$$${of}\:{two}\:{transcedentals}\:{which}\:{are}\:{not} \\ $$$${derivations}\:{of}\:{same}\:{transcedental} \\ $$$${and}\:{give}\:{the}\:{sum}\:{or}\:{product}\:{as}\:{whole} \\ $$$${number}? \\ $$

Commented by Temp last updated on 01/Jul/16

That is an interesting point which I am very interested to find

$$\mathrm{That}\:\mathrm{is}\:\mathrm{an}\:\mathrm{interesting}\:\mathrm{point}\:\mathrm{which} \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{very}\:\mathrm{interested}\:\mathrm{to}\:\mathrm{find} \\ $$

Commented by Rasheed Soomro last updated on 01/Jul/16

An other question is: Are there two transcedentals, (which are not derived from same transcedental/s) whose sum/product is an algebraic number?

$${An}\:{other}\:{question}\:{is}: \\ $$$${Are}\:\:{there}\:{two}\:{transcedentals},\:\left({which}\:{are}\right. \\ $$$$\left.{not}\:{derived}\:{from}\:{same}\:{transcedental}/{s}\right)\:{whose} \\ $$$${sum}/{product}\:{is}\:{an}\:\boldsymbol{{algebraic}}\:\boldsymbol{{number}}? \\ $$

Commented by prakash jain last updated on 01/Jul/16

If sum/product is algebraic the second transcendental number can be derived from the first algebraic number by adding or subtracting the first transcental number. The problem statement implies that that second transcental and first transcendental numbers can be derived using the sum. so the two conditions are contrdictory t_1 +t_2 =n for some n∈Z (1) also second condition is t_1 ≠n−t_1 ∀n∈Z (2) (2) contradicts with (1) same applies for multiplication.

$$\mathrm{If}\:\mathrm{sum}/\mathrm{product}\:\mathrm{is}\:\mathrm{algebraic}\:\mathrm{the}\:\mathrm{second} \\ $$$$\mathrm{transcendental}\:\mathrm{number}\:\mathrm{can}\:\mathrm{be}\:\mathrm{derived}\:\mathrm{from} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{algebraic}\:\mathrm{number}\:\mathrm{by}\:\mathrm{adding}\:\mathrm{or}\:\mathrm{subtracting} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{transcental}\:\mathrm{number}. \\ $$$$\mathrm{The}\:\mathrm{problem}\:\mathrm{statement}\:\mathrm{implies}\:\mathrm{that}\:\mathrm{that} \\ $$$$\mathrm{second}\:\mathrm{transcental}\:\mathrm{and}\:\mathrm{first}\:\mathrm{transcendental} \\ $$$$\mathrm{numbers}\:\mathrm{can}\:\mathrm{be}\:\mathrm{derived}\:\mathrm{using}\:\mathrm{the}\:\mathrm{sum}. \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{two}\:\mathrm{conditions}\:\mathrm{are}\:\mathrm{contrdictory} \\ $$$${t}_{\mathrm{1}} +{t}_{\mathrm{2}} ={n}\:{for}\:{some}\:{n}\in\mathbb{Z}\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{also}\:\mathrm{second}\:\mathrm{condition}\:\mathrm{is} \\ $$$${t}_{\mathrm{1}} \neq{n}−{t}_{\mathrm{1}} \:\forall{n}\in\mathbb{Z}\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{2}\right)\:\mathrm{contradicts}\:\mathrm{with}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{same}\:\mathrm{applies}\:\mathrm{for}\:\mathrm{multiplication}. \\ $$

Commented by Rasheed Soomro last updated on 03/Jul/16

Your comment is decisive!

$${Your}\:{comment}\:{is}\:{decisive}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com