
Question and Answers Forum
Question Number 65004 by mathmax by abdo last updated on 24/Jul/19
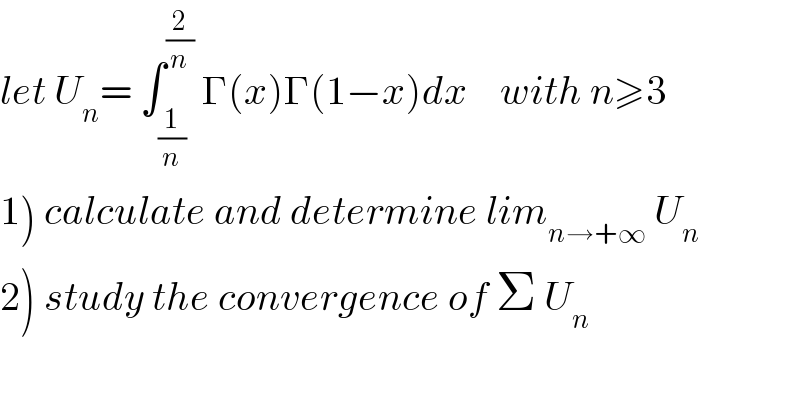
Commented by mathmax by abdo last updated on 24/Jul/19
![1) we have Γ(x).Γ(1−x) =(π/(sin(πx))) ⇒U_n =∫_(1/n) ^(2/n) (π/(sin(πx)))dx =_(πx =t) π ∫_(π/n) ^((2π)/n) (dt/(π sint)) =∫_(π/n) ^((2π)/n) (dt/(sint)) =_(tan((t/2))=u) ∫_(tan((π/(2n)))) ^(tan((π/n))) (1/((2u)/(1+u^2 ))) ((2du)/(1+u^2 )) = ∫_(tan((π/(2n)))) ^(tan((π/n))) (du/u) =[ln∣u∣]_(tan((π/(2n)))) ^(tan((π/n))) =ln∣((tan((π/n)))/(tan((π/(2n)))))∣ ⇒ U_n =ln∣((tan((π/n)))/(tan((π/(2n)))))∣ we have tan((π/n)) ∼(π/n) and tan((π/(2n))) ∼ (π/(2n)) ⇒ ((tan((π/n)))/(tan((π/(2n ))))) ∼(π/n) ((2n)/π) =2 ⇒lim_(n→+∞) U_n =ln(2) 2) lim_(n→+∞) U_n ≠0 ⇒Σ U_n diverges.](Q65079.png)
| ||
Question and Answers Forum | ||
Question Number 65004 by mathmax by abdo last updated on 24/Jul/19 | ||
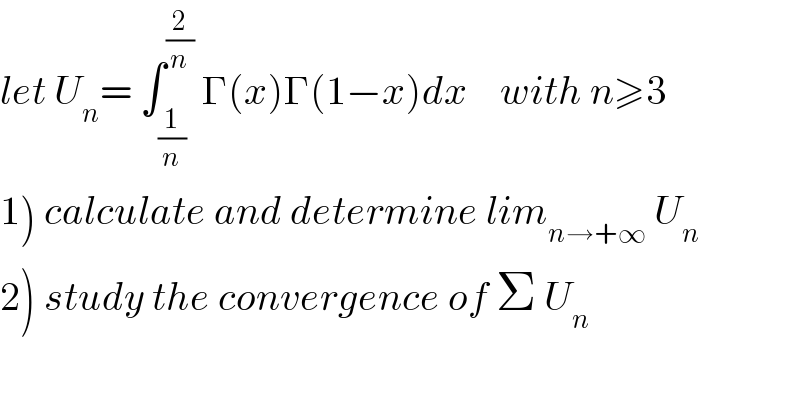 | ||
Commented by mathmax by abdo last updated on 24/Jul/19 | ||
![1) we have Γ(x).Γ(1−x) =(π/(sin(πx))) ⇒U_n =∫_(1/n) ^(2/n) (π/(sin(πx)))dx =_(πx =t) π ∫_(π/n) ^((2π)/n) (dt/(π sint)) =∫_(π/n) ^((2π)/n) (dt/(sint)) =_(tan((t/2))=u) ∫_(tan((π/(2n)))) ^(tan((π/n))) (1/((2u)/(1+u^2 ))) ((2du)/(1+u^2 )) = ∫_(tan((π/(2n)))) ^(tan((π/n))) (du/u) =[ln∣u∣]_(tan((π/(2n)))) ^(tan((π/n))) =ln∣((tan((π/n)))/(tan((π/(2n)))))∣ ⇒ U_n =ln∣((tan((π/n)))/(tan((π/(2n)))))∣ we have tan((π/n)) ∼(π/n) and tan((π/(2n))) ∼ (π/(2n)) ⇒ ((tan((π/n)))/(tan((π/(2n ))))) ∼(π/n) ((2n)/π) =2 ⇒lim_(n→+∞) U_n =ln(2) 2) lim_(n→+∞) U_n ≠0 ⇒Σ U_n diverges.](Q65079.png) | ||