Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 65052 by AnjanDey last updated on 24/Jul/19

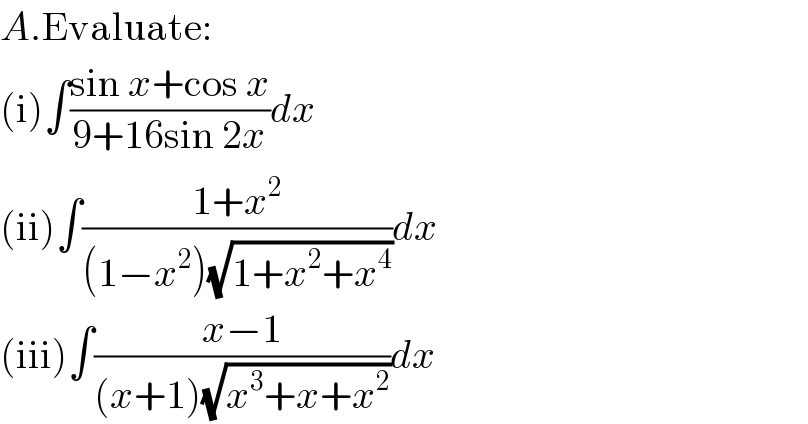
A.Evaluate: (i)∫((sin x+cos x)/(9+16sin 2x))dx (ii)∫((1+x^2 )/((1−x^2 )(√(1+x^2 +x^4 ))))dx (iii)∫((x−1)/((x+1)(√(x^3 +x+x^2 ))))dx

$${A}.\mathrm{Evaluate}: \\ $$$$\left(\mathrm{i}\right)\int\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{9}+\mathrm{16sin}\:\mathrm{2}{x}}{dx} \\ $$$$\left(\mathrm{ii}\right)\int\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }}{dx} \\ $$$$\left(\mathrm{iii}\right)\int\frac{{x}−\mathrm{1}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{3}} +{x}+{x}^{\mathrm{2}} }}{dx} \\ $$

Answered by MJS last updated on 24/Jul/19

(i) ∫((sin x +cos x)/(9+16sin 2x))dx= [t=2arctan x → dx=((2dt)/(t^2 +1))] =−2∫((t^2 −2t−1)/((t^2 −8t+9)(9t^2 +8t+1)))dt= =−18∫((t^2 −2t−1)/((t−4−(√7))(t−4+(√7))(9t+4−(√7))(9t+4+(√7))))dt= =−(1/(40))∫(dt/(t−4−(√7)))−(1/(40))∫(dt/(t−4+(√7)))+(9/(40))∫(dt/(9t+4−(√7)))+(9/(40))∫(dt/(9t+4+(√7)))= =−(1/(40))ln (t−4−(√7)) −(1/(40))ln (t−4+(√7)) +(1/(40))ln (9t+4−(√7)) +(1/(40))ln (9t+4+(√7)) = =(1/(40))ln ((81t^2 +72t+9)/(t^2 −8t+9)) =(1/(40))ln 9((5−4(√2)cos (x+(π/4)))/(5+4(√2)cos (x+(π/4)))) = =(1/(40))ln ∣((5−4(√2)cos (x+(π/4)))/(5+4(√2)cos (x+(π/4))))∣ +C

$$\left(\mathrm{i}\right) \\ $$$$\int\frac{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{\mathrm{9}+\mathrm{16sin}\:\mathrm{2}{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2arctan}\:{x}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=−\mathrm{2}\int\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{\left({t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{9}\right)\left(\mathrm{9}{t}^{\mathrm{2}} +\mathrm{8}{t}+\mathrm{1}\right)}{dt}= \\ $$$$=−\mathrm{18}\int\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{\left({t}−\mathrm{4}−\sqrt{\mathrm{7}}\right)\left({t}−\mathrm{4}+\sqrt{\mathrm{7}}\right)\left(\mathrm{9}{t}+\mathrm{4}−\sqrt{\mathrm{7}}\right)\left(\mathrm{9}{t}+\mathrm{4}+\sqrt{\mathrm{7}}\right)}{dt}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{40}}\int\frac{{dt}}{{t}−\mathrm{4}−\sqrt{\mathrm{7}}}−\frac{\mathrm{1}}{\mathrm{40}}\int\frac{{dt}}{{t}−\mathrm{4}+\sqrt{\mathrm{7}}}+\frac{\mathrm{9}}{\mathrm{40}}\int\frac{{dt}}{\mathrm{9}{t}+\mathrm{4}−\sqrt{\mathrm{7}}}+\frac{\mathrm{9}}{\mathrm{40}}\int\frac{{dt}}{\mathrm{9}{t}+\mathrm{4}+\sqrt{\mathrm{7}}}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{40}}\mathrm{ln}\:\left({t}−\mathrm{4}−\sqrt{\mathrm{7}}\right)\:−\frac{\mathrm{1}}{\mathrm{40}}\mathrm{ln}\:\left({t}−\mathrm{4}+\sqrt{\mathrm{7}}\right)\:+\frac{\mathrm{1}}{\mathrm{40}}\mathrm{ln}\:\left(\mathrm{9}{t}+\mathrm{4}−\sqrt{\mathrm{7}}\right)\:+\frac{\mathrm{1}}{\mathrm{40}}\mathrm{ln}\:\left(\mathrm{9}{t}+\mathrm{4}+\sqrt{\mathrm{7}}\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{40}}\mathrm{ln}\:\frac{\mathrm{81}{t}^{\mathrm{2}} +\mathrm{72}{t}+\mathrm{9}}{{t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{9}}\:=\frac{\mathrm{1}}{\mathrm{40}}\mathrm{ln}\:\mathrm{9}\frac{\mathrm{5}−\mathrm{4}\sqrt{\mathrm{2}}\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{5}+\mathrm{4}\sqrt{\mathrm{2}}\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{40}}\mathrm{ln}\:\mid\frac{\mathrm{5}−\mathrm{4}\sqrt{\mathrm{2}}\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{5}+\mathrm{4}\sqrt{\mathrm{2}}\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}\mid\:+{C} \\ $$

Answered by MJS last updated on 24/Jul/19

(ii) ∫((1+x^2 )/((1−x^2 )(√(1+x^2 +x^4 ))))dx= [t=2arctan x → dx=((1+x^2 )/2)dt] =(√2)∫(dt/(cos t (√(7+cos 2t))))= [u=tan t → dt=cos^2 t du] =∫(du/(√(3u^2 +4)))=((√3)/3)ln ((√3)u+(√(3u^2 +4))) = =((√3)/3)ln ((2(√3)sin t +(√(14+2cos 2t)))/(2cos t)) = =((√3)/3)ln (2(((√3)x+(√(x^4 +x^2 +1)))/(1−x^2 ))) = =((√3)/3)ln ∣(((√3)x+(√(x^4 +x^2 +1)))/(1−x^2 ))∣ +C

$$\left(\mathrm{ii}\right) \\ $$$$\int\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2arctan}\:{x}\:\rightarrow\:{dx}=\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{2}}{dt}\right] \\ $$$$=\sqrt{\mathrm{2}}\int\frac{{dt}}{\mathrm{cos}\:{t}\:\sqrt{\mathrm{7}+\mathrm{cos}\:\mathrm{2}{t}}}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{tan}\:{t}\:\rightarrow\:{dt}=\mathrm{cos}^{\mathrm{2}} \:{t}\:{du}\right] \\ $$$$=\int\frac{{du}}{\sqrt{\mathrm{3}{u}^{\mathrm{2}} +\mathrm{4}}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{ln}\:\left(\sqrt{\mathrm{3}}{u}+\sqrt{\mathrm{3}{u}^{\mathrm{2}} +\mathrm{4}}\right)\:= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{ln}\:\frac{\mathrm{2}\sqrt{\mathrm{3}}\mathrm{sin}\:{t}\:+\sqrt{\mathrm{14}+\mathrm{2cos}\:\mathrm{2}{t}}}{\mathrm{2cos}\:{t}}\:= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{ln}\:\left(\mathrm{2}\frac{\sqrt{\mathrm{3}}{x}+\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{1}−{x}^{\mathrm{2}} }\right)\:= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{3}}{x}+\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{1}−{x}^{\mathrm{2}} }\mid\:+{C} \\ $$$$ \\ $$

Answered by Tanmay chaudhury last updated on 25/Jul/19

1)∫((sinx+cosx)/(9+16(1−1+sin2x))) ∫((d(sinx−cosx))/(9+16−16(1−sin2x))) ∫((d(sinx−cosx))/(25−16(sinx−cosx)^2 )) (1/(16))∫((d(sinx−cosx))/(((5/4))^2 −(sinx−cosx)^2 )) (1/(16))×(1/(2×(5/4)))×ln((((5/4)+(sinx−cosx))/((5/4)−(sinx−cosx))))+c

$$\left.\mathrm{1}\right)\int\frac{{sinx}+{cosx}}{\mathrm{9}+\mathrm{16}\left(\mathrm{1}−\mathrm{1}+{sin}\mathrm{2}{x}\right)} \\ $$$$\int\frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{9}+\mathrm{16}−\mathrm{16}\left(\mathrm{1}−{sin}\mathrm{2}{x}\right)} \\ $$$$\int\frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{25}−\mathrm{16}\left({sinx}−{cosx}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\int\frac{{d}\left({sinx}−{cosx}\right)}{\left(\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} −\left({sinx}−{cosx}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}×\frac{\mathrm{1}}{\mathrm{2}×\frac{\mathrm{5}}{\mathrm{4}}}×{ln}\left(\frac{\frac{\mathrm{5}}{\mathrm{4}}+\left({sinx}−{cosx}\right)}{\frac{\mathrm{5}}{\mathrm{4}}−\left({sinx}−{cosx}\right)}\right)+{c} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by Tanmay chaudhury last updated on 25/Jul/19

ii)∫(((1/x^2 )+1)/(((1/x)−x)(√((1/x^2 )+1+x^2 ))))dx ∫((d(x−(1/x)))/(−(x−(1/x))(√((x−(1/x))^2 +3)))) x−(1/x)=(1/k) d(x−(1/x))=−(1/k^2 )dk ∫((−dk)/(k^2 ×((−1)/k)×(√((1/k^2 )+3)))) ∫(dk/(√(1+3k^2 ))) (1/(√3))∫(dk/(√(k^2 +(1/3)))) (1/(√3))×ln(k+(√(k^2 +(1/3))) )+c (1/(√3))ln[(x−(1/x))+(√((x−(1/x))^2 +(1/3))) ]+c

$$\left.{ii}\right)\int\frac{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}{\left(\frac{\mathrm{1}}{{x}}−{x}\right)\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}+{x}^{\mathrm{2}} }}{dx} \\ $$$$\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{−\left({x}−\frac{\mathrm{1}}{{x}}\right)\sqrt{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}} \\ $$$${x}−\frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{{k}} \\ $$$${d}\left({x}−\frac{\mathrm{1}}{{x}}\right)=−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }{dk} \\ $$$$\int\frac{−{dk}}{{k}^{\mathrm{2}} ×\frac{−\mathrm{1}}{{k}}×\sqrt{\frac{\mathrm{1}}{{k}^{\mathrm{2}} }+\mathrm{3}}} \\ $$$$\int\frac{{dk}}{\sqrt{\mathrm{1}+\mathrm{3}{k}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\int\frac{{dk}}{\sqrt{{k}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}}} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}×{ln}\left({k}+\sqrt{{k}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}}\:\right)+{c} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}{ln}\left[\left({x}−\frac{\mathrm{1}}{{x}}\right)+\sqrt{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}}\:\right]+{c} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com