Question and Answers Forum
Question Number 65054 by behi83417@gmail.com last updated on 24/Jul/19
![{ (((√(x+y))+(√(x−y))=a)),((x^2 +y^2 =b [a,b∈R])) :}](Q65054.png)
Commented by behi83417@gmail.com last updated on 24/Jul/19
![thanks in advance proph. Abdo. [u+v=a⇒u^2 +v^2 +2uv=a^2 ]please check.](Q65072.png)
Commented by mathmax by abdo last updated on 24/Jul/19

Answered by MJS last updated on 24/Jul/19
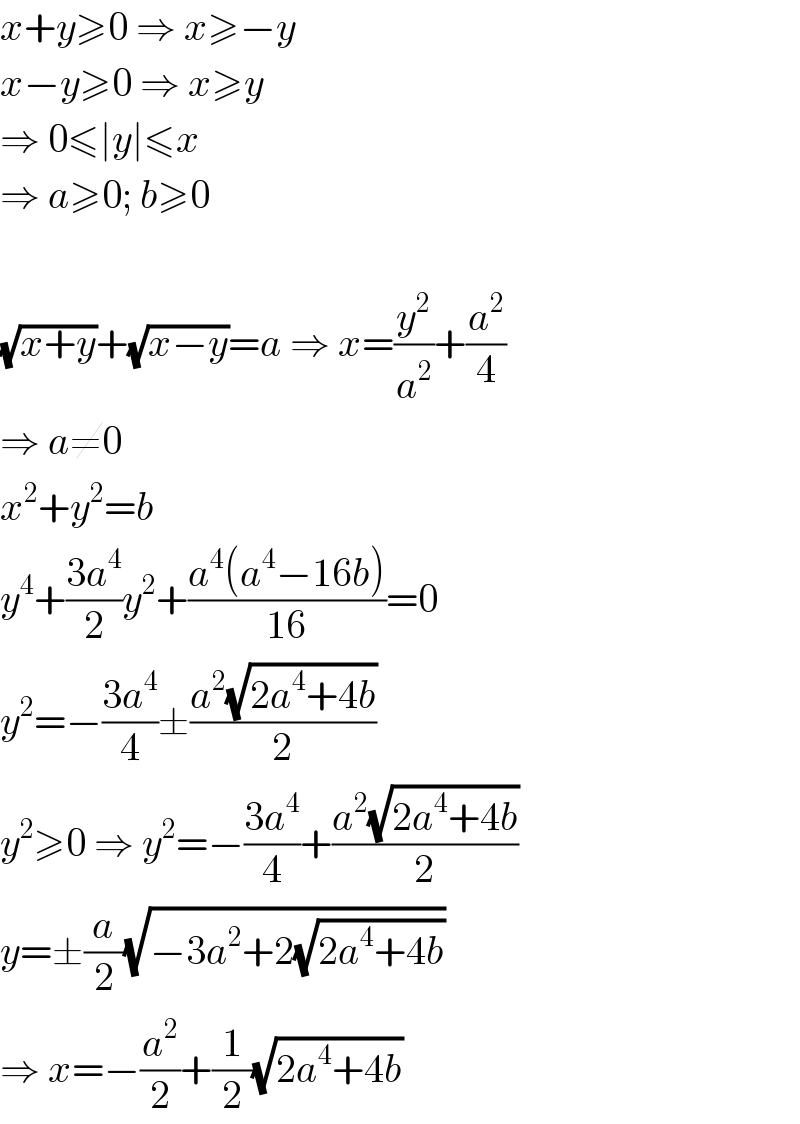
Commented by MJS last updated on 24/Jul/19

Commented by MJS last updated on 24/Jul/19
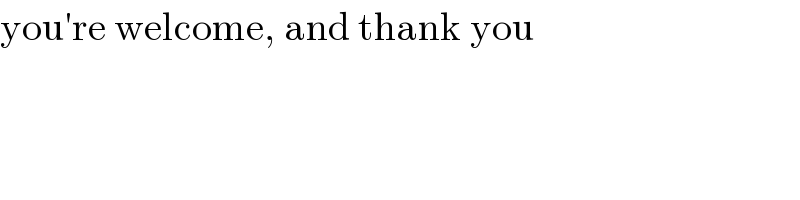
Commented by behi83417@gmail.com last updated on 24/Jul/19

Answered by mr W last updated on 24/Jul/19
![x+y=p x−y=q ⇒(√p)+(√q)=a>0 (x+y)^2 +(x−y)^2 =2(x^2 +y^2 ) ⇒p^2 +q^2 =2b let P=(√p) ,Q=(√q) P+Q=a⇒Q=a−P P^4 +Q^4 =2b⇒P^4 +(a−P)^4 =2b ⇒2P^4 −4aP^3 +6a^2 P^2 −4a^3 P+a^4 −2b=0 let λ=(P/a) ⇒λ^4 −2λ^3 +3λ^2 −2λ+((1/2)−(b/a^4 ))=0 ⇒λ^4 −2λ^3 +3λ^2 −2λ+δ=0 ⇒λ_(1,2) =(1/2)[1±(√(4(√(1−δ))−3))] ⇒λ_(2,3) =(1/2)[1±i(√(4(√(1−δ))+3))] P_(1,2) =aλ=(a/2)[1±(√(4(√(1−δ))−3))] Q_(1,2) =a−(a/2)[1±(√(4(√(1−δ))−3))]=(a/2)[1∓(√(4(√(1−δ))−3))] P_(3,4) =aλ=(a/2)[1±i(√(4(√(1−δ))+3))] Q_(3,4) =a−(a/2)[1±i(√(4(√(1−δ))+3))]=(a/2)[1∓i(√(4(√(1−δ))+3))] x=((p+q)/2)=((P^2 +Q^2 )/2) y=((p−q)/2)=((P^2 −Q^2 )/2) ⇒x_(1,2) =(a^2 /8){[1±(√(4(√(1−δ))−3))]^2 +[1∓(√(4(√(1−δ))−3))]^2 } ⇒x_(1,2) =(1/2)a^2 (2(√(1−δ))−1) ⇒x_(1,2) =(1/2)[(√(2(a^4 +2b)))−a^2 ] ⇒x_(3,4) =(a^2 /8){[1±i(√(4(√(1−δ))+3))]^2 +[1∓i(√(4(√(1−δ))+3))]^2 } ⇒x_(3,4) =−(a^2 /2)(2(√(1−δ))+1) ⇒x_(3,4) =−(1/2)[(√(2(a^4 +2b)))+a^2 ] ⇒y_(1,2) =(a^2 /8){[1±(√(4(√(1−δ))−3))]^2 −[1∓(√(4(√(1−δ))−3))]^2 } ⇒y_(1,2) =±(a^2 /2)(√(4(√(1−δ))−3)) ⇒y_(1,2) =±(a/2)(√(2(√(2(a^4 +2b)))−3a^2 )) ⇒y_(3,4) =(a^2 /8){[1±i(√(4(√(1−δ))+3))]^2 −[1∓i(√(4(√(1−δ))+3))]^2 } ⇒y_(3,4) =±((a^2 i)/2)(√(4(√(1−δ))+3)) ⇒y_(3,4) =±((ai)/2)(√(2(√(2(a^4 +2b)))+3a^2 ))](Q65076.png)
Commented by behi83417@gmail.com last updated on 24/Jul/19

Commented by mr W last updated on 25/Jul/19