Question Number 65062 by ajfour last updated on 24/Jul/19
$${If}\:\:{x}^{\mathrm{4}} +{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$$\Rightarrow\:{t}^{\mathrm{4}} +{At}^{\mathrm{2}} +{B}=\mathrm{0} \\ $$$${Find}\:{A}\:{and}\:{B}. \\ $$
Commented by MJS last updated on 24/Jul/19
$$\mathrm{I}\:\mathrm{once}\:\mathrm{posted}\:\mathrm{that}\:\mathrm{matrix}\:\mathrm{method}\:\mathrm{by} \\ $$$$\mathrm{Tschirnhaus}...\:\mathrm{cannot}\:\mathrm{find}\:\mathrm{it}\:\mathrm{right}\:\mathrm{now}, \\ $$$$\mathrm{must}\:\mathrm{be}\:\mathrm{somewhere}\:\mathrm{on}\:\mathrm{this}\:\mathrm{forum} \\ $$$$\mathrm{it}\:\mathrm{should}\:\mathrm{help}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$
Commented by MJS last updated on 24/Jul/19
$$\mathrm{found}\:\mathrm{it}:\:\mathrm{question}\:\mathrm{54775} \\ $$
Commented by MJS last updated on 24/Jul/19
$$\mathrm{you}'\mathrm{ll}\:\mathrm{have}\:\mathrm{to}\:\mathrm{adapt}\:\mathrm{it}\:\mathrm{to}\:\mathrm{remove}\:\mathrm{the}\:\mathrm{linear} \\ $$$$\mathrm{term}\:\mathrm{but}\:\mathrm{it}\:\mathrm{looks}\:\mathrm{possible} \\ $$
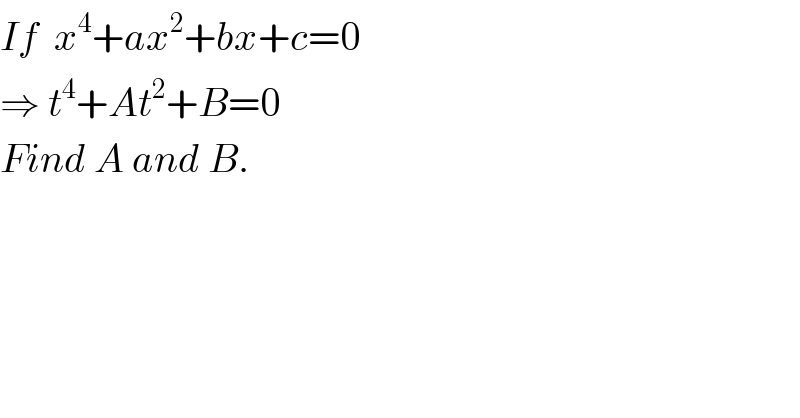
Commented by MJS last updated on 25/Jul/19
$$...\mathrm{you}\:\mathrm{also}\:\mathrm{need}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{how}\:\mathrm{to}\:\mathrm{use}\:\mathrm{the} \\ $$$$\mathrm{method}\:\mathrm{with}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{4}^{\mathrm{th}} \:\mathrm{degree}... \\ $$$$\mathrm{maybe}\:\mathrm{you}\:\mathrm{can}\:\mathrm{find}\:\mathrm{something}\:\mathrm{on}\:\mathrm{the}\:\mathrm{web} \\ $$
Commented by ajfour last updated on 25/Jul/19
$${MjS}\:{Sir},\:{thanks}\:{for}\:{your} \\ $$$${sincere}\:{suggestions}\:{and}\:{yes} \\ $$$${my}\:{method}\:{is}\:{hopelessly} \\ $$$${complicated}.. \\ $$
Answered by ajfour last updated on 26/Jul/19
![let x=((pt+q)/(t+1)) ⇒ p^4 t^4 +4p^3 qt^3 +6p^2 q^2 t^2 +4pq^3 t+q^4 +a(p^2 t^2 +2pqt+q^2 )(t^2 +2t+1) +b(pt+q)(t^3 +3t^2 +3t+1) +c(t^4 +4t^3 +6t^2 +4t+1)=0 ⇒ (p^4 +ap^2 +bp+c)t^4 + (4p^3 q+2ap^2 +2apq+3bp+bq+4c)t^3 +(6p^2 q^2 +ap^2 +4apq+aq^2 + 3bp+3bq+6c)t^2 + (4pq^3 +2apq+2aq^2 +bp+3bq+4c)t +(q^4 +aq^2 +bq+c)=0 since coefficients of t^3 , t have to be zero, ⇒ 4p^3 q+2ap^2 +2apq+3bp+bq+4c=0 ....(I) 4pq^3 +2apq+2aq^2 +bp+3bq+4c=0 ....(II) subtracting ⇒ 2pq(p^2 −q^2 )+a(p^2 −q^2 )+b(p−q)=0 And as p≠q , ⇒ 2pq(p+q)+a(p+q)+b=0 ...(i) Adding (I),(II) 2pq(p^2 +q^2 )+a(p^2 +q^2 )+2apq+ 2b(p+q)+4c=0 .....(ii) let p+q=s , pq=m transforming (i)&(ii) ________________________ s(2m+a)+b=0 ....(A) (2m+a)(s^2 −2m)+ 2am+2bs+4c=0 ....(B) ________________________ (A) ⇒ m=−(((as+b)/(2s))) Substituting in (B) −(b/s)(s^2 +((as+b)/s))−((a(as+b))/s) +2bs+4c=0 ⇒ ((b(as+b))/s^2 )+((a(as+b))/s)=bs+4c ________________________ ⇒ bs^3 +(4c−a^2 )s^2 −2abs−b^2 =0 s is obtained from this eq. m=−(((as+b)/(2s))) p, q are then roots of quadratic z^2 −sz+m=0 ________________________ Now (p^4 +ap^2 +bp+c)t^4 + +(6p^2 q^2 +ap^2 +4apq+aq^2 + 3bp+3bq+6c)t^2 + +(q^4 +aq^2 +bq+c)=0 ⇒ t^4 +(((6p^2 q^2 +ap^2 +4apq+aq^2 +3bp+3bq+6c)/(p^4 +ap^2 +bp+c)))t^2 +((q^4 +aq^2 +bq+c)/(p^4 +ap^2 +bp+c)) = 0 t^4 +[((6p^2 q^2 +a(p+q)^2 +2apq+3b(p+q))/(p^4 +ap^2 +bp+c))]t^2 +((q^4 +aq^2 +bq+c)/(p^4 +ap^2 +bp++c)) = 0 ⇒ t^4 +[((6m^2 +as^2 +2am+3bs)/(f(p)))]t^2 +((f(q))/(f(p)))=0 x=((pt+q)/(t+1)) .](Q65065.png)
$${let}\:\:{x}=\frac{{pt}+{q}}{{t}+\mathrm{1}} \\ $$$$\Rightarrow\:{p}^{\mathrm{4}} {t}^{\mathrm{4}} +\mathrm{4}{p}^{\mathrm{3}} {qt}^{\mathrm{3}} +\mathrm{6}{p}^{\mathrm{2}} {q}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{4}{pq}^{\mathrm{3}} {t}+{q}^{\mathrm{4}} \\ $$$$\:\:\:+{a}\left({p}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{2}{pqt}+{q}^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right) \\ $$$$\:\:\:+{b}\left({pt}+{q}\right)\left({t}^{\mathrm{3}} +\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{t}+\mathrm{1}\right) \\ $$$$\:\:\:+{c}\left({t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{3}} +\mathrm{6}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:\left({p}^{\mathrm{4}} +{ap}^{\mathrm{2}} +{bp}+{c}\right){t}^{\mathrm{4}} + \\ $$$$\left(\mathrm{4}{p}^{\mathrm{3}} {q}+\mathrm{2}{ap}^{\mathrm{2}} +\mathrm{2}{apq}+\mathrm{3}{bp}+{bq}+\mathrm{4}{c}\right){t}^{\mathrm{3}} \\ $$$$+\left(\mathrm{6}{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{ap}^{\mathrm{2}} +\mathrm{4}{apq}+{aq}^{\mathrm{2}} +\right. \\ $$$$\left.\:\:\:\:\:\:\mathrm{3}{bp}+\mathrm{3}{bq}+\mathrm{6}{c}\right){t}^{\mathrm{2}} + \\ $$$$\left(\mathrm{4}{pq}^{\mathrm{3}} +\mathrm{2}{apq}+\mathrm{2}{aq}^{\mathrm{2}} +{bp}+\mathrm{3}{bq}+\mathrm{4}{c}\right){t} \\ $$$$+\left({q}^{\mathrm{4}} +{aq}^{\mathrm{2}} +{bq}+{c}\right)=\mathrm{0} \\ $$$$ \\ $$$${since}\:{coefficients}\:{of}\:{t}^{\mathrm{3}} \:,\:{t}\:{have} \\ $$$${to}\:{be}\:{zero},\:\Rightarrow \\ $$$$\mathrm{4}{p}^{\mathrm{3}} {q}+\mathrm{2}{ap}^{\mathrm{2}} +\mathrm{2}{apq}+\mathrm{3}{bp}+{bq}+\mathrm{4}{c}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:....\left({I}\right) \\ $$$$\mathrm{4}{pq}^{\mathrm{3}} +\mathrm{2}{apq}+\mathrm{2}{aq}^{\mathrm{2}} +{bp}+\mathrm{3}{bq}+\mathrm{4}{c}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:....\left({II}\right) \\ $$$${subtracting}\:\Rightarrow \\ $$$$\mathrm{2}{pq}\left({p}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)+{a}\left({p}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)+{b}\left({p}−{q}\right)=\mathrm{0} \\ $$$${And}\:{as}\:\:{p}\neq{q}\:,\:\Rightarrow \\ $$$$\mathrm{2}{pq}\left({p}+{q}\right)+{a}\left({p}+{q}\right)+{b}=\mathrm{0}\:\:\:\:...\left({i}\right) \\ $$$${Adding}\:\left({I}\right),\left({II}\right) \\ $$$$\mathrm{2}{pq}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)+{a}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)+\mathrm{2}{apq}+ \\ $$$$\:\:\mathrm{2}{b}\left({p}+{q}\right)+\mathrm{4}{c}=\mathrm{0}\:\:\:\:\:\:.....\left({ii}\right) \\ $$$$ \\ $$$${let}\:\:{p}+{q}={s}\:,\:{pq}={m} \\ $$$${transforming}\:\left({i}\right)\&\left({ii}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${s}\left(\mathrm{2}{m}+{a}\right)+{b}=\mathrm{0}\:\:\:\:\:\:\:....\left({A}\right) \\ $$$$\left(\mathrm{2}{m}+{a}\right)\left({s}^{\mathrm{2}} −\mathrm{2}{m}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}{am}+\mathrm{2}{bs}+\mathrm{4}{c}=\mathrm{0}\:\:\:\:....\left({B}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\left({A}\right)\:\Rightarrow\:\:\:\:{m}=−\left(\frac{{as}+{b}}{\mathrm{2}{s}}\right) \\ $$$${Substituting}\:{in}\:\left({B}\right) \\ $$$$\:\:−\frac{{b}}{{s}}\left({s}^{\mathrm{2}} +\frac{{as}+{b}}{{s}}\right)−\frac{{a}\left({as}+{b}\right)}{{s}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}{bs}+\mathrm{4}{c}=\mathrm{0} \\ $$$$\Rightarrow\:\:\frac{{b}\left({as}+{b}\right)}{{s}^{\mathrm{2}} }+\frac{{a}\left({as}+{b}\right)}{{s}}={bs}+\mathrm{4}{c} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\:{bs}^{\mathrm{3}} +\left(\mathrm{4}{c}−{a}^{\mathrm{2}} \right){s}^{\mathrm{2}} −\mathrm{2}{abs}−{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:{s}\:{is}\:{obtained}\:{from}\:{this}\:{eq}. \\ $$$$\:\:\:\:\:\:\:{m}=−\left(\frac{{as}+{b}}{\mathrm{2}{s}}\right) \\ $$$$\:{p},\:{q}\:{are}\:{then}\:{roots}\:{of}\:{quadratic} \\ $$$$\:\:\:\:\:{z}^{\mathrm{2}} −{sz}+{m}=\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${Now} \\ $$$$\:\left({p}^{\mathrm{4}} +{ap}^{\mathrm{2}} +{bp}+{c}\right){t}^{\mathrm{4}} + \\ $$$$+\left(\mathrm{6}{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{ap}^{\mathrm{2}} +\mathrm{4}{apq}+{aq}^{\mathrm{2}} +\right. \\ $$$$\left.\:\:\:\:\:\:\mathrm{3}{bp}+\mathrm{3}{bq}+\mathrm{6}{c}\right){t}^{\mathrm{2}} + \\ $$$$+\left({q}^{\mathrm{4}} +{aq}^{\mathrm{2}} +{bq}+{c}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:{t}^{\mathrm{4}} +\left(\frac{\mathrm{6}{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{ap}^{\mathrm{2}} +\mathrm{4}{apq}+{aq}^{\mathrm{2}} +\mathrm{3}{bp}+\mathrm{3}{bq}+\mathrm{6}{c}}{{p}^{\mathrm{4}} +{ap}^{\mathrm{2}} +{bp}+{c}}\right){t}^{\mathrm{2}} \\ $$$$\:\:\:+\frac{{q}^{\mathrm{4}} +{aq}^{\mathrm{2}} +{bq}+{c}}{{p}^{\mathrm{4}} +{ap}^{\mathrm{2}} +{bp}+{c}}\:=\:\mathrm{0} \\ $$$$\boldsymbol{{t}}^{\mathrm{4}} +\left[\frac{\mathrm{6}\boldsymbol{{p}}^{\mathrm{2}} \boldsymbol{{q}}^{\mathrm{2}} +\boldsymbol{{a}}\left(\boldsymbol{{p}}+\boldsymbol{{q}}\right)^{\mathrm{2}} +\mathrm{2}\boldsymbol{{apq}}+\mathrm{3}\boldsymbol{{b}}\left(\boldsymbol{{p}}+\boldsymbol{{q}}\right)}{\boldsymbol{{p}}^{\mathrm{4}} +\boldsymbol{{ap}}^{\mathrm{2}} +\boldsymbol{{bp}}+\boldsymbol{{c}}}\right]\boldsymbol{{t}}^{\mathrm{2}} \\ $$$$\:\:\:+\frac{\boldsymbol{{q}}^{\mathrm{4}} +\boldsymbol{{aq}}^{\mathrm{2}} +\boldsymbol{{bq}}+\boldsymbol{{c}}}{\boldsymbol{{p}}^{\mathrm{4}} +\boldsymbol{{ap}}^{\mathrm{2}} +\boldsymbol{{bp}}++\boldsymbol{{c}}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{t}^{\mathrm{4}} +\left[\frac{\mathrm{6}{m}^{\mathrm{2}} +{as}^{\mathrm{2}} +\mathrm{2}{am}+\mathrm{3}{bs}}{{f}\left({p}\right)}\right]{t}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{{f}\left({q}\right)}{{f}\left({p}\right)}=\mathrm{0} \\ $$$$\:\:\:{x}=\frac{{pt}+{q}}{{t}+\mathrm{1}}\:\:.\:\:\:\:\:\: \\ $$