
Question Number 6512 by Rasheed Soomro last updated on 30/Jun/16
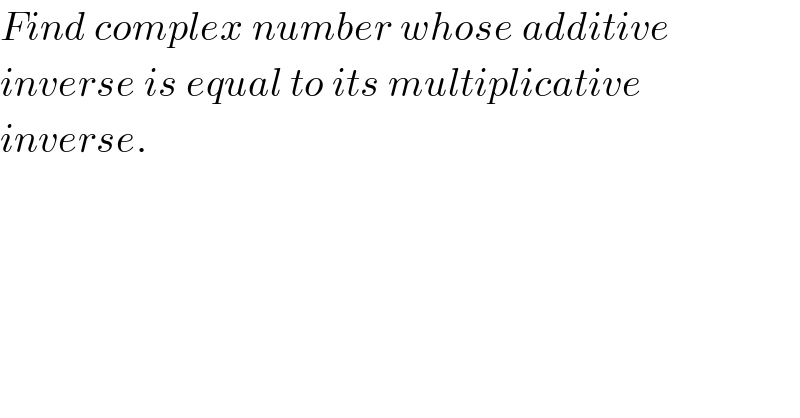
$${Find}\:{complex}\:{number}\:{whose}\:{additive}\: \\ $$$${inverse}\:{is}\:{equal}\:{to}\:{its}\:{multiplicative} \\ $$$${inverse}. \\ $$
Commented by Temp last updated on 30/Jun/16
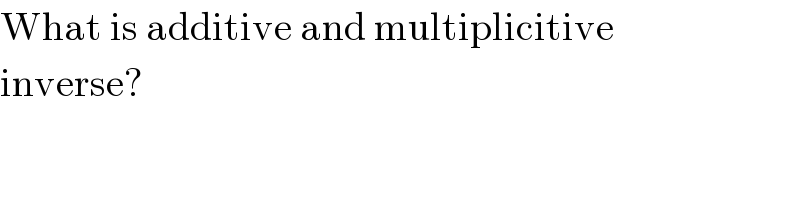
$$\mathrm{What}\:\mathrm{is}\:\mathrm{additive}\:\mathrm{and}\:\mathrm{multiplicitive} \\ $$$$\mathrm{inverse}? \\ $$
Commented by Rasheed Soomro last updated on 30/Jun/16
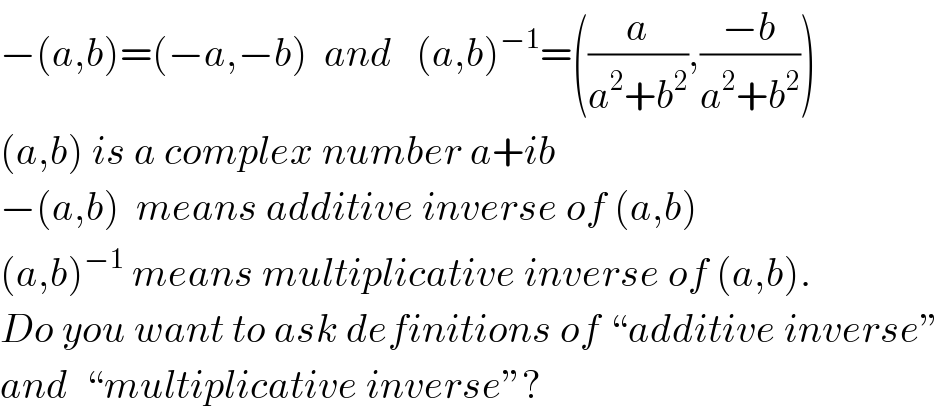
$$−\left({a},{b}\right)=\left(−{a},−{b}\right)\:\:{and}\:\:\:\left({a},{b}\right)^{−\mathrm{1}} =\left(\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} },\frac{−{b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right) \\ $$$$\left({a},{b}\right)\:{is}\:{a}\:{complex}\:{number}\:{a}+{ib} \\ $$$$−\left({a},{b}\right)\:\:{means}\:{additive}\:{inverse}\:{of}\:\left({a},{b}\right) \\ $$$$\left({a},{b}\right)^{−\mathrm{1}} \:{means}\:{multiplicative}\:{inverse}\:{of}\:\left({a},{b}\right). \\ $$$${Do}\:{you}\:{want}\:{to}\:{ask}\:{definitions}\:{of}\:``{additive}\:{inverse}'' \\ $$$${and}\:\:``{multiplicative}\:{inverse}''? \\ $$
Answered by Yozzii last updated on 30/Jun/16
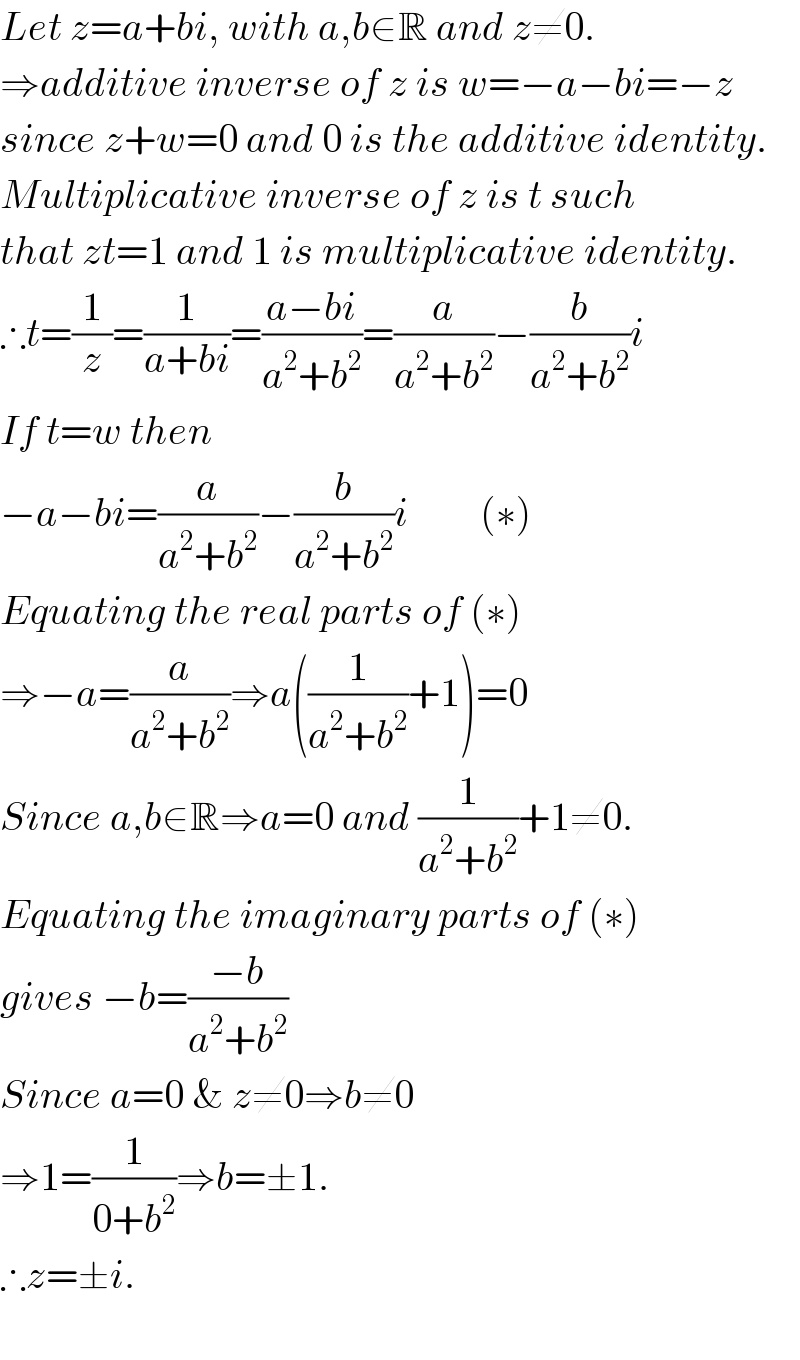
$${Let}\:{z}={a}+{bi},\:{with}\:{a},{b}\in\mathbb{R}\:{and}\:{z}\neq\mathrm{0}. \\ $$$$\Rightarrow{additive}\:{inverse}\:{of}\:{z}\:{is}\:{w}=−{a}−{bi}=−{z} \\ $$$${since}\:{z}+{w}=\mathrm{0}\:{and}\:\mathrm{0}\:{is}\:{the}\:{additive}\:{identity}. \\ $$$${Multiplicative}\:{inverse}\:{of}\:{z}\:{is}\:{t}\:{such} \\ $$$${that}\:{zt}=\mathrm{1}\:{and}\:\mathrm{1}\:{is}\:{multiplicative}\:{identity}. \\ $$$$\therefore{t}=\frac{\mathrm{1}}{{z}}=\frac{\mathrm{1}}{{a}+{bi}}=\frac{{a}−{bi}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−\frac{{b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{i} \\ $$$${If}\:{t}={w}\:{then} \\ $$$$−{a}−{bi}=\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−\frac{{b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{i}\:\:\:\:\:\:\:\:\:\left(\ast\right) \\ $$$${Equating}\:{the}\:{real}\:{parts}\:{of}\:\left(\ast\right) \\ $$$$\Rightarrow−{a}=\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\Rightarrow{a}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\mathrm{1}\right)=\mathrm{0} \\ $$$${Since}\:{a},{b}\in\mathbb{R}\Rightarrow{a}=\mathrm{0}\:{and}\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\mathrm{1}\neq\mathrm{0}. \\ $$$${Equating}\:{the}\:{imaginary}\:{parts}\:{of}\:\left(\ast\right) \\ $$$${gives}\:−{b}=\frac{−{b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${Since}\:{a}=\mathrm{0}\:\&\:{z}\neq\mathrm{0}\Rightarrow{b}\neq\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}=\frac{\mathrm{1}}{\mathrm{0}+{b}^{\mathrm{2}} }\Rightarrow{b}=\pm\mathrm{1}. \\ $$$$\therefore{z}=\pm{i}. \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 30/Jun/16

$$\mathcal{TH}\alpha{n}\mathcal{X}! \\ $$
Answered by Rasheed Soomro last updated on 01/Jul/16
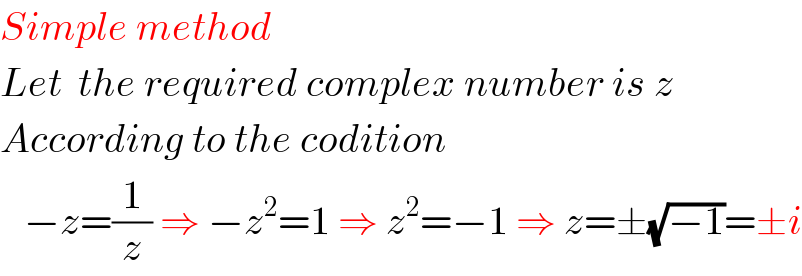
$${Simple}\:{method} \\ $$$${Let}\:\:{the}\:{required}\:{complex}\:{number}\:{is}\:{z} \\ $$$${According}\:{to}\:{the}\:{codition} \\ $$$$\:\:\:−{z}=\frac{\mathrm{1}}{{z}}\:\Rightarrow\:−{z}^{\mathrm{2}} =\mathrm{1}\:\Rightarrow\:{z}^{\mathrm{2}} =−\mathrm{1}\:\Rightarrow\:{z}=\pm\sqrt{−\mathrm{1}}=\pm{i} \\ $$
