Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 66693 by mathmax by abdo last updated on 18/Aug/19

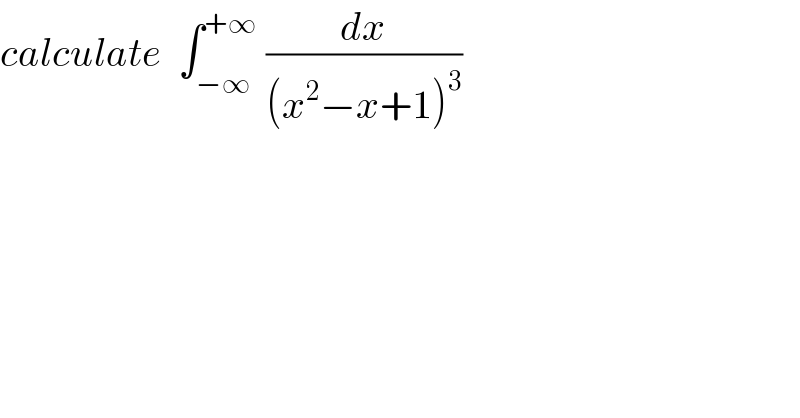
calculate ∫_(−∞) ^(+∞) (dx/((x^2 −x+1)^3 ))

$${calculate}\:\:\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$

Commented by mathmax by abdo last updated on 19/Aug/19

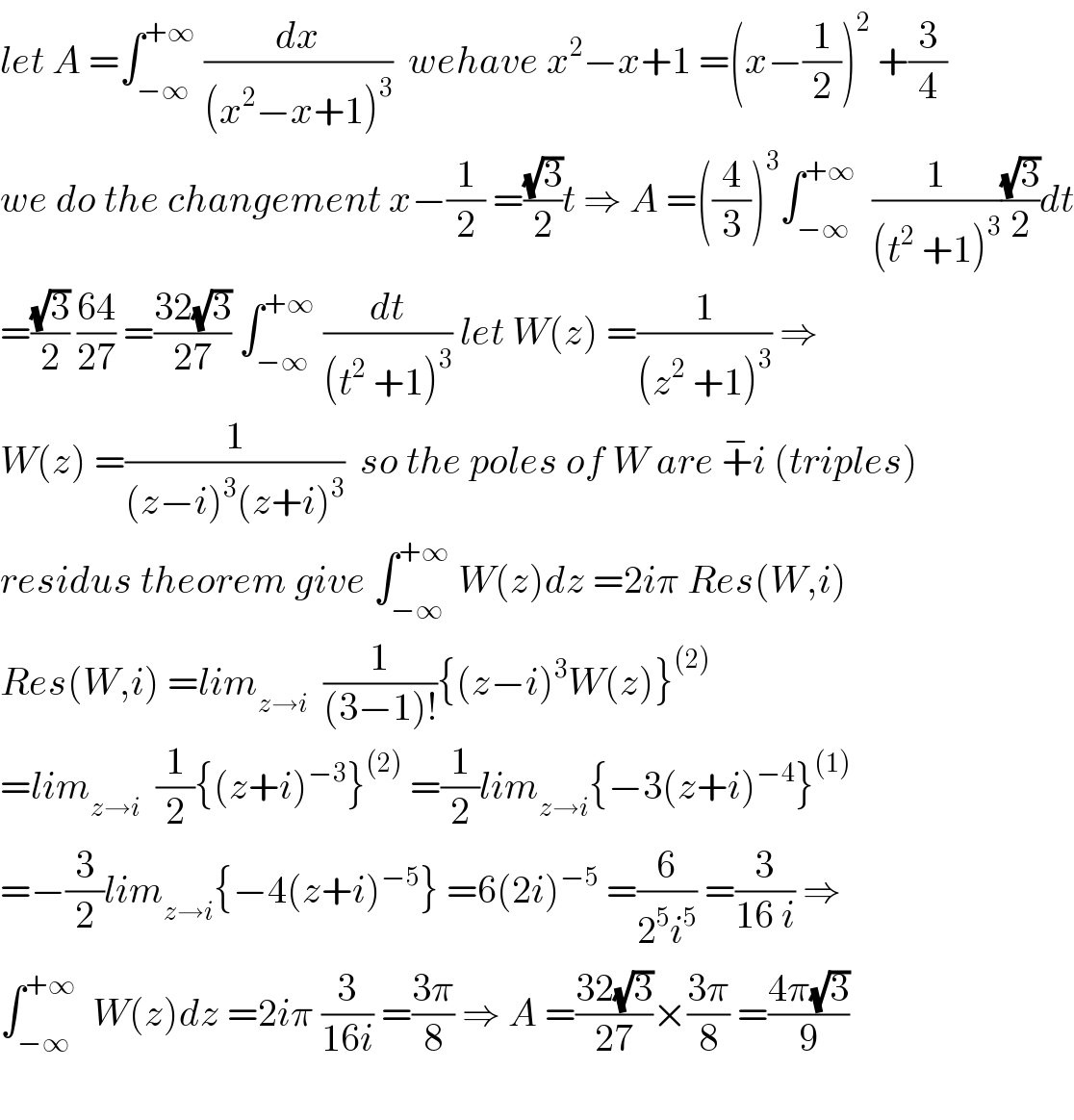
let A =∫_(−∞) ^(+∞) (dx/((x^2 −x+1)^3 )) wehave x^2 −x+1 =(x−(1/2))^2 +(3/4) we do the changement x−(1/2) =((√3)/2)t ⇒ A =((4/3))^3 ∫_(−∞) ^(+∞) (1/((t^2 +1)^3 ))((√3)/2)dt =((√3)/2) ((64)/(27)) =((32(√3))/(27)) ∫_(−∞) ^(+∞) (dt/((t^2 +1)^3 )) let W(z) =(1/((z^2 +1)^3 )) ⇒ W(z) =(1/((z−i)^3 (z+i)^3 )) so the poles of W are +^− i (triples) residus theorem give ∫_(−∞) ^(+∞) W(z)dz =2iπ Res(W,i) Res(W,i) =lim_(z→i) (1/((3−1)!)){(z−i)^3 W(z)}^((2)) =lim_(z→i) (1/2){(z+i)^(−3) }^((2)) =(1/2)lim_(z→i) {−3(z+i)^(−4) }^((1)) =−(3/2)lim_(z→i) {−4(z+i)^(−5) } =6(2i)^(−5) =(6/(2^5 i^5 )) =(3/(16 i)) ⇒ ∫_(−∞) ^(+∞) W(z)dz =2iπ (3/(16i)) =((3π)/8) ⇒ A =((32(√3))/(27))×((3π)/8) =((4π(√3))/9)

$${let}\:{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{3}} }\:\:{wehave}\:{x}^{\mathrm{2}} −{x}+\mathrm{1}\:=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${we}\:{do}\:{the}\:{changement}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}\:\Rightarrow\:{A}\:=\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{3}} \int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\frac{\mathrm{64}}{\mathrm{27}}\:=\frac{\mathrm{32}\sqrt{\mathrm{3}}}{\mathrm{27}}\:\int_{−\infty} ^{+\infty} \:\frac{{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:{let}\:{W}\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$${W}\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}−{i}\right)^{\mathrm{3}} \left({z}+{i}\right)^{\mathrm{3}} }\:\:{so}\:{the}\:{poles}\:{of}\:{W}\:{are}\:\overset{−} {+}{i}\:\left({triples}\right) \\ $$$${residus}\:{theorem}\:{give}\:\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left({W},{i}\right) \\ $$$${Res}\left({W},{i}\right)\:={lim}_{{z}\rightarrow{i}} \:\:\frac{\mathrm{1}}{\left(\mathrm{3}−\mathrm{1}\right)!}\left\{\left({z}−{i}\right)^{\mathrm{3}} {W}\left({z}\right)\right\}^{\left(\mathrm{2}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\left({z}+{i}\right)^{−\mathrm{3}} \right\}^{\left(\mathrm{2}\right)} \:=\frac{\mathrm{1}}{\mathrm{2}}{lim}_{{z}\rightarrow{i}} \left\{−\mathrm{3}\left({z}+{i}\right)^{−\mathrm{4}} \right\}^{\left(\mathrm{1}\right)} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}{lim}_{{z}\rightarrow{i}} \left\{−\mathrm{4}\left({z}+{i}\right)^{−\mathrm{5}} \right\}\:=\mathrm{6}\left(\mathrm{2}{i}\right)^{−\mathrm{5}} \:=\frac{\mathrm{6}}{\mathrm{2}^{\mathrm{5}} {i}^{\mathrm{5}} }\:=\frac{\mathrm{3}}{\mathrm{16}\:{i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{\mathrm{3}}{\mathrm{16}{i}}\:=\frac{\mathrm{3}\pi}{\mathrm{8}}\:\Rightarrow\:{A}\:=\frac{\mathrm{32}\sqrt{\mathrm{3}}}{\mathrm{27}}×\frac{\mathrm{3}\pi}{\mathrm{8}}\:=\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$$$ \\ $$

Answered by mind is power last updated on 18/Aug/19

let f(a)=∫_(−∞) ^(+∞) (dx/((x^2 −x+a))) withe a>(1/4) f(a)=∫_(−∞) ^(+∞) (dx/(((x−(1/2))^2 +((4a−1)/4)))) f(a)=∫_(−∞) ^(+∞) (dx/(((((2x−1)/(√((4a−1)))))^2 +1))).(4/(4a−1)) f(a)=(2/(√(4a−1)))∫_(−∞) ^(+∞) (d((2x−1)/(√(4a−1)))/(((((2x−1)/((√(4a−1))))))^2 +1))) =f(a)=(2/(√(4a−1)))[arctg(((2x−1)/(√(4a−1))))]_(−∞) ^(+∞) =((2π)/(√(4a−1))) f′(a)=(d/da)∫_(−∞) ^(+∞) (1/(x^2 −x+a))dx=∫_(−∞) ^(+∞) −(dx/((x^2 −x+a)^2 )) f′′(a)=∫_(−∞) ^(+∞) ((2dx)/((a+x+x^2 )^3 )) ∫_(−∞) ^(+∞) ((2dx)/((1+x+x^2 )^3 ))=f′′(1) f′(a)=(((2π)/(√(4a−1))))′=−4π(4a−1)^((−3)/2) f′′(a)=24π(4a−1)^(−(5/2)) ..>f′′(1)=24π(3)^(−(5/2)) ==>2∫_(−∞) ^(+∞) (dx/((1+x+x^2 )^3 ))=((24π)/(9(√3)))==>∫_(−∞) ^(+∞) (dx/((1+x+x^2 )^3 ))=((4π)/(3(√3)))

$${let}\:{f}\left({a}\right)=\int_{−\infty} ^{+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+{a}\right)}\:{withe}\:{a}>\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${f}\left({a}\right)=\int_{−\infty} ^{+\infty} \frac{{dx}}{\left(\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{4}{a}−\mathrm{1}}{\mathrm{4}}\right)} \\ $$$${f}\left({a}\right)=\int_{−\infty} ^{+\infty} \frac{{dx}}{\left(\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\left(\mathrm{4}{a}−\mathrm{1}\right)}}\right)^{\mathrm{2}} +\mathrm{1}\right)}.\frac{\mathrm{4}}{\mathrm{4}{a}−\mathrm{1}} \\ $$$${f}\left({a}\right)=\frac{\mathrm{2}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}\int_{−\infty} ^{+\infty} \frac{{d}\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}}{\left(\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\left.\sqrt{\mathrm{4}{a}−\mathrm{1}}\right)}\right)^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$={f}\left({a}\right)=\frac{\mathrm{2}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}\left[{arctg}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}\right)\right]_{−\infty} ^{+\infty} =\frac{\mathrm{2}\pi}{\sqrt{\mathrm{4}{a}−\mathrm{1}}} \\ $$$${f}'\left({a}\right)=\frac{{d}}{{da}}\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}+{a}}{dx}=\int_{−\infty} ^{+\infty} −\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+{a}\right)^{\mathrm{2}} } \\ $$$${f}''\left({a}\right)=\int_{−\infty} ^{+\infty} \frac{\mathrm{2}{dx}}{\left({a}+{x}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$\int_{−\infty} ^{+\infty} \frac{\mathrm{2}{dx}}{\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }={f}''\left(\mathrm{1}\right) \\ $$$${f}'\left({a}\right)=\left(\frac{\mathrm{2}\pi}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}\right)'=−\mathrm{4}\pi\left(\mathrm{4}{a}−\mathrm{1}\right)^{\frac{−\mathrm{3}}{\mathrm{2}}} \\ $$$${f}''\left({a}\right)=\mathrm{24}\pi\left(\mathrm{4}{a}−\mathrm{1}\right)^{−\frac{\mathrm{5}}{\mathrm{2}}} ..>{f}''\left(\mathrm{1}\right)=\mathrm{24}\pi\left(\mathrm{3}\right)^{−\frac{\mathrm{5}}{\mathrm{2}}} \\ $$$$==>\mathrm{2}\int_{−\infty} ^{+\infty} \frac{{dx}}{\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }=\frac{\mathrm{24}\pi}{\mathrm{9}\sqrt{\mathrm{3}}}==>\int_{−\infty} ^{+\infty} \frac{{dx}}{\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }=\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com