
Question and Answers Forum
Question Number 65133 by turbo msup by abdo last updated on 25/Jul/19
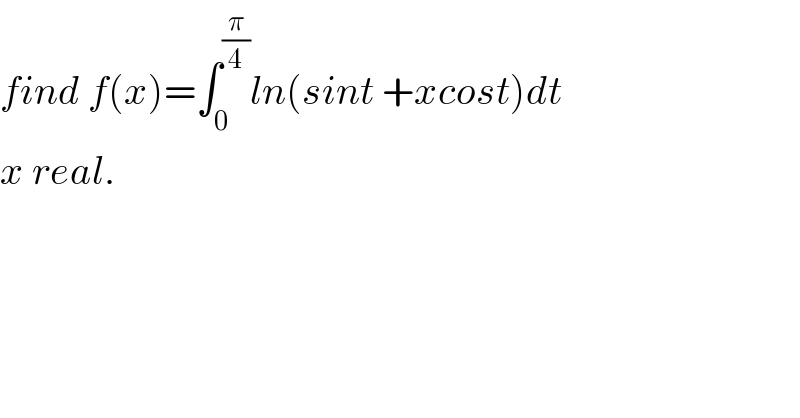
Commented by mathmax by abdo last updated on 27/Jul/19
![we have f^′ (x) =∫_0 ^(π/4) ((cost)/(sint +xcost))dt changement tan((t/2)) =u give f^′ (x) = ∫_0 ^((√2)−1) (((1−u^2 )/(1+u^2 ))/(((2u)/(1+u^2 )) +x((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) =2∫_0 ^((√2)−1) ((1−u^2 )/((1+u^2 )(2u +x−xu^2 )))du =2 ∫_0 ^((√2)−1) ((u^2 −1)/((u^2 +1)(xu^2 −2u −x)))du let decompose F(u) =((u^2 −1)/((u^2 +1)(xu^2 −2u −x))) xu^2 −2u−x =0→Δ^′ =1+x^2 >0 ⇒u_1 (x)=((1+(√(1+x^2 )))/x) u_2 (x)=((1−(√(1+x^2 )))/x) ⇒F(u) =((u^2 −1)/(x(u^2 +1)(u−u_1 )(u−u_2 ))) F(u) =(a/(u−u_1 )) +(b/(u−u_2 )) +((cu +d)/(u^2 +1)) a =lim_(u→u_1 ) (u−u_(1 ) )F(u) =((u_1 ^2 −1)/(x(u_1 ^2 +1)(u_1 −u_2 ))) b =lim_(u→u_2 ) (u−u_2 )F(u) =((u_2 ^2 −1)/(x(u_2 ^2 +1)(u_2 −u_1 ))) lim_(u→+∞) uF(u) =0 =a+b +c ⇒c =−a−b F(0) =(1/x) =−(a/u_1 ) −(b/u_2 ) +d ⇒d =(1/x) +(a/u_1 ) +(b/u_2 ) ⇒ F(u) =(a/(u−u_1 )) +(b/(u−u_2 )) +((−(a+b)u +(1/x)+(a/u_1 )+(b/u_2 ))/(u^2 +1)) ⇒ f^′ (x) =2 ∫_0 ^((√2)−1) ((a/(u−u_1 )) +(b/(u−u_2 )) +((−(a+b)u +λ_x )/(u^(2 ) +1)) )du =2a [ln∣u−u_1 ∣]_0 ^((√2)−1) +2b [ln∣u−u_2 ∣]_0 ^((√2)−1) −(a+b)[ln(u^2 +1)]_0 ^((√2)−1) +2λ_x [arctanu]_0 ^((√2)−1) =2a ln∣(((√2)−1−u_1 )/u_1 )∣ +2b ln∣(((√2)−1−u_2 )/u_2 )∣−(a+b)ln( ((√2)−1)^2 +1) +2λ_x (π/8) ⇒ f(x) =2a ∫ ln∣(((√2)−1−u_1 (x))/(u_1 (x)))∣dx +2b∫ ln∣(((√2)−1−u_2 (x))/(u_2 (x)))∣dx −(a+b)ln(4−2(√2))x +(π/4) ∫ λ_x dx +c ....be continued....](Q65283.png)
| ||
Question and Answers Forum | ||
Question Number 65133 by turbo msup by abdo last updated on 25/Jul/19 | ||
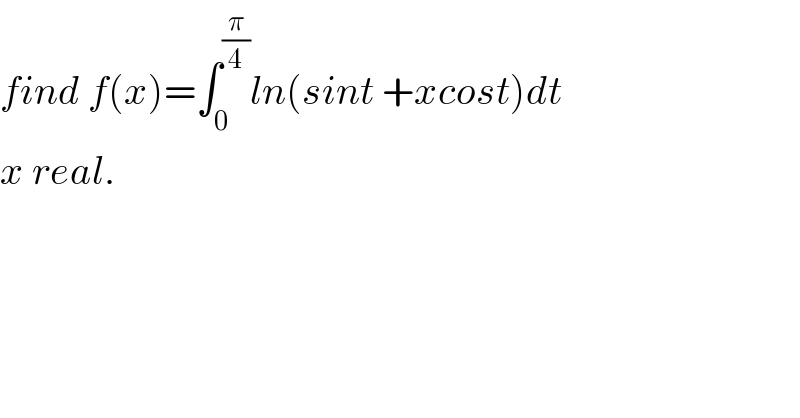 | ||
Commented by mathmax by abdo last updated on 27/Jul/19 | ||
![we have f^′ (x) =∫_0 ^(π/4) ((cost)/(sint +xcost))dt changement tan((t/2)) =u give f^′ (x) = ∫_0 ^((√2)−1) (((1−u^2 )/(1+u^2 ))/(((2u)/(1+u^2 )) +x((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) =2∫_0 ^((√2)−1) ((1−u^2 )/((1+u^2 )(2u +x−xu^2 )))du =2 ∫_0 ^((√2)−1) ((u^2 −1)/((u^2 +1)(xu^2 −2u −x)))du let decompose F(u) =((u^2 −1)/((u^2 +1)(xu^2 −2u −x))) xu^2 −2u−x =0→Δ^′ =1+x^2 >0 ⇒u_1 (x)=((1+(√(1+x^2 )))/x) u_2 (x)=((1−(√(1+x^2 )))/x) ⇒F(u) =((u^2 −1)/(x(u^2 +1)(u−u_1 )(u−u_2 ))) F(u) =(a/(u−u_1 )) +(b/(u−u_2 )) +((cu +d)/(u^2 +1)) a =lim_(u→u_1 ) (u−u_(1 ) )F(u) =((u_1 ^2 −1)/(x(u_1 ^2 +1)(u_1 −u_2 ))) b =lim_(u→u_2 ) (u−u_2 )F(u) =((u_2 ^2 −1)/(x(u_2 ^2 +1)(u_2 −u_1 ))) lim_(u→+∞) uF(u) =0 =a+b +c ⇒c =−a−b F(0) =(1/x) =−(a/u_1 ) −(b/u_2 ) +d ⇒d =(1/x) +(a/u_1 ) +(b/u_2 ) ⇒ F(u) =(a/(u−u_1 )) +(b/(u−u_2 )) +((−(a+b)u +(1/x)+(a/u_1 )+(b/u_2 ))/(u^2 +1)) ⇒ f^′ (x) =2 ∫_0 ^((√2)−1) ((a/(u−u_1 )) +(b/(u−u_2 )) +((−(a+b)u +λ_x )/(u^(2 ) +1)) )du =2a [ln∣u−u_1 ∣]_0 ^((√2)−1) +2b [ln∣u−u_2 ∣]_0 ^((√2)−1) −(a+b)[ln(u^2 +1)]_0 ^((√2)−1) +2λ_x [arctanu]_0 ^((√2)−1) =2a ln∣(((√2)−1−u_1 )/u_1 )∣ +2b ln∣(((√2)−1−u_2 )/u_2 )∣−(a+b)ln( ((√2)−1)^2 +1) +2λ_x (π/8) ⇒ f(x) =2a ∫ ln∣(((√2)−1−u_1 (x))/(u_1 (x)))∣dx +2b∫ ln∣(((√2)−1−u_2 (x))/(u_2 (x)))∣dx −(a+b)ln(4−2(√2))x +(π/4) ∫ λ_x dx +c ....be continued....](Q65283.png) | ||