
Question Number 6519 by benny last updated on 30/Jun/16
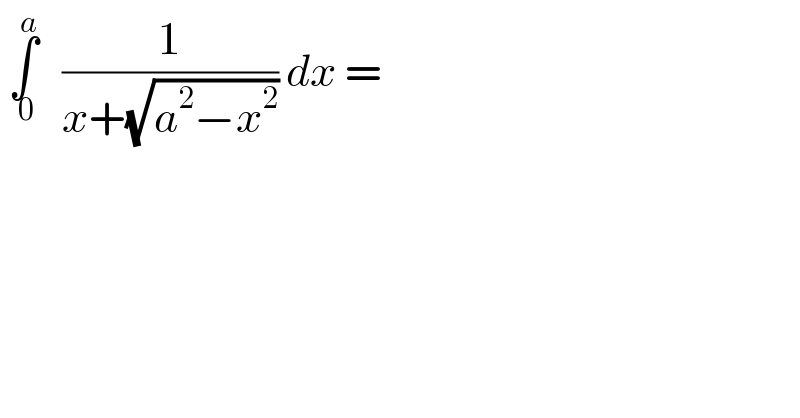
$$\:\underset{\:\mathrm{0}} {\overset{{a}} {\int}}\:\:\:\frac{\mathrm{1}}{{x}+\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}\:{dx}\:= \\ $$
Commented by Tawakalitu. last updated on 30/Jun/16

$$\frac{\Pi}{\mathrm{4}} \\ $$
Commented by Tawakalitu. last updated on 01/Jul/16
![x = a sint dx = a cost dt ∴ ∫(dx/(x + (√(a^2 − x^2 )))) = ∫((a cost dt)/(a sint + (√(a^2 − a^2 sin^2 t)))) = ∫((a cost dt)/(a sint + (√(a^2 − a^2 (1 − cos^2 t))))) = ∫((a cost dt)/(a sint + (√(a^2 − a^2 + a^2 cos^2 t)))) = ∫((a cost dt)/(a sint + (√(a^2 cos^2 t)))) = ∫((a cost dt)/(a sint + a cost)) = ∫((a cost dt)/(a(sint + cost))) = ∫((cost dt)/(sint + cost)) = ∫(((1/2) × 2 cost dt)/(sint + cost)) = ∫(((1/2) × (cost + cost) dt)/(sint + cost)) = ∫(((1/2) × (cost + sint + cost − sint) dt)/(sint + cost)) = ∫(((1/2)(cost + sint)dt + (1/2)(cost − sint)dt)/(cost + sint)) = ∫(1/2) × ((cost + sint)/(cost + sint)) dt + ∫(1/2) × ((cost − sint)/(cost + sint)) dt = ∫(1/2) dt + ∫(1/2) × ((cost − sint)/(cost + sint)) dt let u = cost + sint, (du/dt) = − sint + cost , du = (cost − sint) dt = ∫(1/2) dt + ∫(1/2) × (du/u) = (1/2)t + ln(u) + C = (1/2)t + ln(cost + sint) + C But, x = a sint .... x = 0, a 0 = a sint ⇒ sint = 0 ⇒ t = sin^(−1) 0 ⇒ t = 0 Again, a = a sint ⇒ sint = 1 ⇒ t = sin^(−1) (1) ⇒ t = 90 ⇒ t = (Π/2) [(1/2)t + ln(sint + cost) + C]_0 ^(Π/2) = (1/2)((Π/2))+ln(sin(Π/2)+cos(Π/2))+C − [(1/2)(0)+ln(sin0+cos0) + C] = (Π/4) + ln(1+0)+C−0−ln(0+1)−C = (Π/4) + ln(1) + C − 0 − ln(1) − C = (Π/4) DONE ! Force × Distance = ISE](Q6526.png)
$${x}\:=\:{a}\:{sint}\: \\ $$$${dx}\:=\:{a}\:{cost}\:{dt}\: \\ $$$$\therefore\:\int\frac{{dx}}{{x}\:+\:\sqrt{{a}^{\mathrm{2}} \:−\:{x}^{\mathrm{2}} }}\: \\ $$$$=\:\int\frac{{a}\:{cost}\:{dt}}{{a}\:{sint}\:+\:\sqrt{{a}^{\mathrm{2}} \:−\:{a}^{\mathrm{2}} \:{sin}^{\mathrm{2}} {t}}}\:\:=\:\int\frac{{a}\:{cost}\:{dt}}{{a}\:{sint}\:+\:\sqrt{{a}^{\mathrm{2}} \:−\:{a}^{\mathrm{2}} \:\left(\mathrm{1}\:−\:{cos}^{\mathrm{2}} {t}\right)}}\:=\:\int\frac{{a}\:{cost}\:{dt}}{{a}\:{sint}\:+\:\sqrt{{a}^{\mathrm{2}} \:−\:{a}^{\mathrm{2}} \:+\:{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {t}}} \\ $$$$=\:\int\frac{{a}\:{cost}\:{dt}}{{a}\:{sint}\:+\:\sqrt{{a}^{\mathrm{2}} \:{cos}^{\mathrm{2}} {t}}} \\ $$$$=\:\int\frac{{a}\:{cost}\:{dt}}{{a}\:{sint}\:+\:{a}\:{cost}}\:\:=\:\:\int\frac{{a}\:{cost}\:{dt}}{{a}\left({sint}\:+\:{cost}\right)} \\ $$$$=\:\int\frac{{cost}\:{dt}}{{sint}\:+\:{cost}} \\ $$$$=\:\int\frac{\frac{\mathrm{1}}{\mathrm{2}}\:×\:\mathrm{2}\:{cost}\:{dt}}{{sint}\:+\:{cost}} \\ $$$$=\:\int\frac{\frac{\mathrm{1}}{\mathrm{2}}\:×\:\left({cost}\:+\:{cost}\right)\:{dt}}{{sint}\:+\:{cost}} \\ $$$$=\:\int\frac{\frac{\mathrm{1}}{\mathrm{2}}\:×\:\left({cost}\:+\:{sint}\:+\:{cost}\:−\:{sint}\right)\:{dt}}{{sint}\:+\:{cost}}\: \\ $$$$=\:\int\frac{\frac{\mathrm{1}}{\mathrm{2}}\left({cost}\:+\:{sint}\right){dt}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left({cost}\:−\:{sint}\right){dt}}{{cost}\:+\:{sint}} \\ $$$$=\:\int\frac{\mathrm{1}}{\mathrm{2}}\:×\:\frac{{cost}\:+\:{sint}}{{cost}\:+\:{sint}}\:{dt}\:+\:\int\frac{\mathrm{1}}{\mathrm{2}}\:×\:\frac{{cost}\:−\:{sint}}{{cost}\:+\:{sint}}\:{dt} \\ $$$$=\:\int\frac{\mathrm{1}}{\mathrm{2}}\:{dt}\:+\:\int\frac{\mathrm{1}}{\mathrm{2}}\:×\:\frac{{cost}\:−\:{sint}}{{cost}\:+\:{sint}}\:{dt} \\ $$$${let}\:{u}\:=\:{cost}\:+\:{sint},\:\:\:\frac{{du}}{{dt}}\:=\:−\:{sint}\:+\:{cost}\:,\:{du}\:=\:\left({cost}\:−\:{sint}\right)\:{dt} \\ $$$$=\:\int\frac{\mathrm{1}}{\mathrm{2}}\:{dt}\:+\:\int\frac{\mathrm{1}}{\mathrm{2}}\:×\:\frac{{du}}{{u}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}{t}\:+\:{ln}\left({u}\right)\:+\:{C} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}{t}\:+\:{ln}\left({cost}\:+\:{sint}\right)\:+\:{C} \\ $$$${But},\:{x}\:=\:{a}\:{sint}\:\:\:....\:\:\:{x}\:=\:\mathrm{0},\:{a} \\ $$$$\mathrm{0}\:=\:{a}\:{sint}\:\Rightarrow\:{sint}\:=\:\mathrm{0}\:\Rightarrow\:{t}\:=\:{sin}^{−\mathrm{1}} \mathrm{0}\:\Rightarrow\:{t}\:=\:\mathrm{0} \\ $$$${Again}, \\ $$$${a}\:=\:{a}\:{sint}\:\Rightarrow\:{sint}\:=\:\mathrm{1}\:\Rightarrow\:{t}\:=\:{sin}^{−\mathrm{1}} \left(\mathrm{1}\right)\:\Rightarrow\:{t}\:=\:\mathrm{90}\:\Rightarrow\:{t}\:=\:\frac{\Pi}{\mathrm{2}} \\ $$$$\left[\frac{\mathrm{1}}{\mathrm{2}}{t}\:+\:{ln}\left({sint}\:+\:{cost}\right)\:+\:{C}\right]_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\Pi}{\mathrm{2}}\right)+{ln}\left({sin}\frac{\Pi}{\mathrm{2}}+{cos}\frac{\Pi}{\mathrm{2}}\right)+{C}\:−\:\left[\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}\right)+{ln}\left({sin}\mathrm{0}+{cos}\mathrm{0}\right)\:+\:{C}\right] \\ $$$$=\:\frac{\Pi}{\mathrm{4}}\:+\:{ln}\left(\mathrm{1}+\mathrm{0}\right)+{C}−\mathrm{0}−{ln}\left(\mathrm{0}+\mathrm{1}\right)−{C} \\ $$$$=\:\frac{\Pi}{\mathrm{4}}\:+\:{ln}\left(\mathrm{1}\right)\:+\:{C}\:−\:\mathrm{0}\:−\:{ln}\left(\mathrm{1}\right)\:−\:{C} \\ $$$$=\:\frac{\Pi}{\mathrm{4}}\: \\ $$$$ \\ $$$${DONE}\:! \\ $$$${Force}\:×\:{Distance}\:=\:{ISE} \\ $$$$ \\ $$
Commented by sandy_suhendra last updated on 01/Jul/16
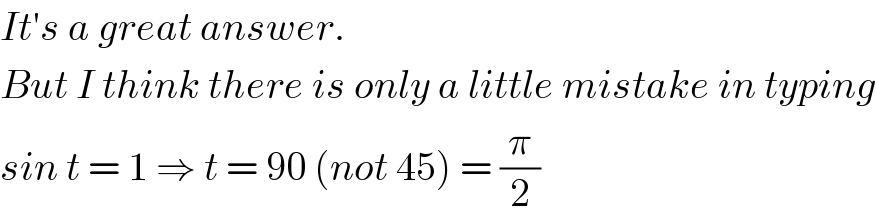
$${It}'{s}\:{a}\:{great}\:{answer}.\: \\ $$$${But}\:{I}\:{think}\:{there}\:{is}\:{only}\:{a}\:{little}\:{mistake}\:{in}\:{typing} \\ $$$${sin}\:{t}\:=\:\mathrm{1}\:\Rightarrow\:{t}\:=\:\mathrm{90}\:\left({not}\:\mathrm{45}\right)\:=\:\frac{\pi}{\mathrm{2}} \\ $$
Commented by Tawakalitu. last updated on 01/Jul/16

$${corrected}.\:\mathrm{10}{Q} \\ $$
