
Question and Answers Forum
Question Number 65192 by naka3546 last updated on 26/Jul/19
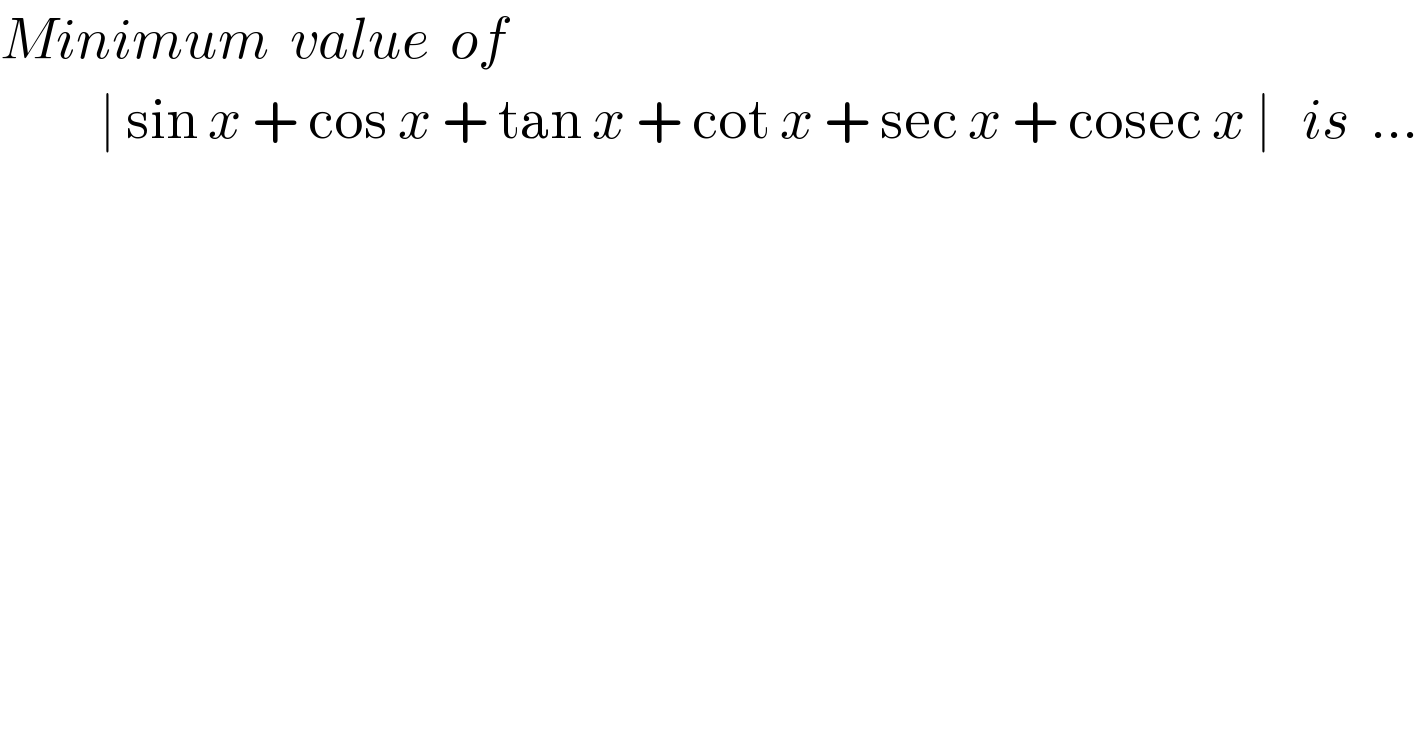
Answered by Tanmay chaudhury last updated on 26/Jul/19

| ||
Question and Answers Forum | ||
Question Number 65192 by naka3546 last updated on 26/Jul/19 | ||
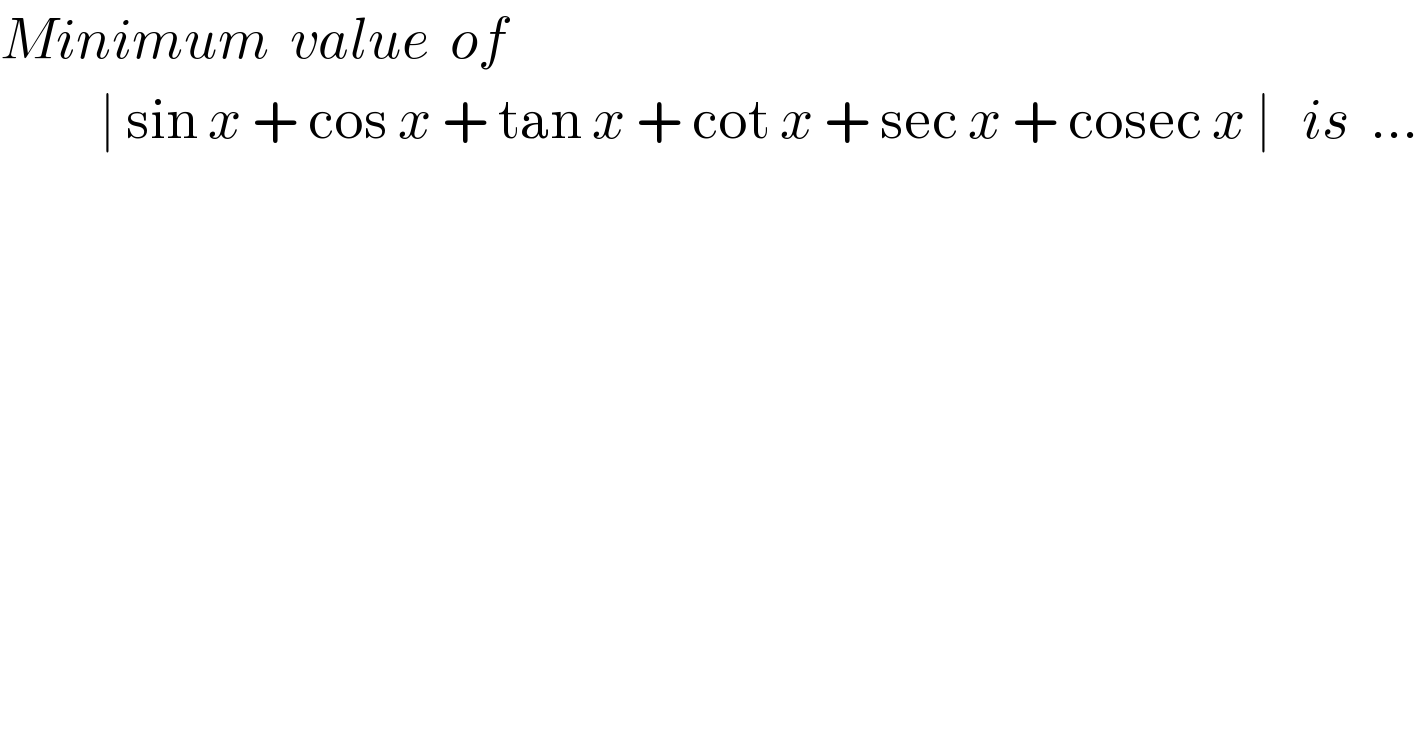 | ||
Answered by Tanmay chaudhury last updated on 26/Jul/19 | ||
 | ||
| ||