
Question Number 65287 by mathmax by abdo last updated on 27/Jul/19
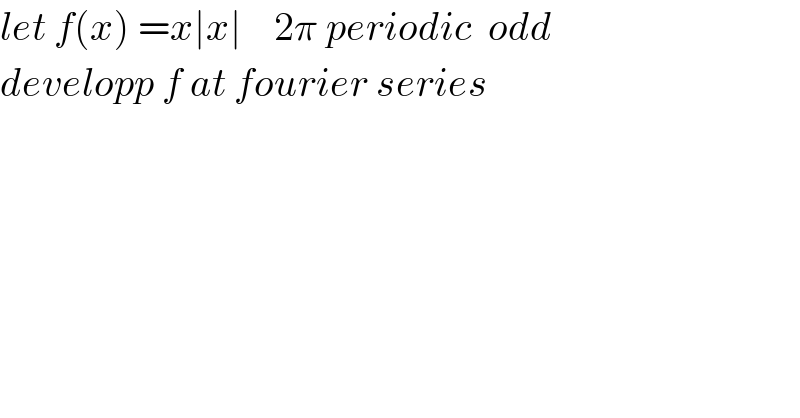
$${let}\:{f}\left({x}\right)\:={x}\mid{x}\mid\:\:\:\:\mathrm{2}\pi\:{periodic}\:\:{odd} \\ $$$${developp}\:{f}\:{at}\:{fourier}\:{series} \\ $$
Commented by mathmax by abdo last updated on 28/Jul/19
![f(x) =Σ_(n=1) ^∞ a_n sin(nx) with a_n =(2/T) ∫_([T]) f(x)sin(nx)dx =(2/(2π)) ∫_(−π) ^π x∣x∣ sin(nx)dx =(2/π) ∫_0 ^π x^2 sin(nx)dx ⇒ (π/2)a_n =∫_0 ^π x^2 sin(nx)dx by parts u =x^2 and v^′ =sin(nx) ⇒ (π/2)a_n =[−(x^2 /n)cos(nx)]_0 ^π −∫_0 ^π (2x)(−(1/n))cos(nx)dx =−(π^2 /n)(−1)^n +(2/n) ∫_0 ^π x cos(nx)dx again by parts ∫_0 ^π x cos(nx)dx =[(x/n)sin(nx)]_0 ^π −∫_0 ^π (1/n)sin(nx)dx =−(1/n) ∫_0 ^π sin(nx)dx =(1/n^2 )[cos(nx)]_0 ^π =(1/n^2 )((−1)^n −1) ⇒ (π/2)a_n =−(π^2 /n)(−1)^n +(2/n^3 ) {(−1)^n −1} a_n =(2/π){−(π^2 /n)(−1)^n +(2/n^3 ){ (−1)^n −1)} =−2π (((−1)^n )/n) +(4/(πn^3 )){ (−1)^n −1} ⇒ x∣x∣ =Σ_(n=1) ^∞ (−2π (((−1)^n )/n) +(4/(πn^3 )){(−1)^n −1})sin(nx) =−2π Σ_(n=1) ^∞ (((−1)^n )/n)sin(nx) +(4/π) Σ_(n=1) ^∞ (((−1)^n −1)/n^3 )sin(nx)](Q65338.png)
$${f}\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{a}_{{n}} {sin}\left({nx}\right)\:{with}\:{a}_{{n}} =\frac{\mathrm{2}}{{T}}\:\int_{\left[{T}\right]} \:\:{f}\left({x}\right){sin}\left({nx}\right){dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}\pi}\:\int_{−\pi} ^{\pi} \:{x}\mid{x}\mid\:{sin}\left({nx}\right){dx}\:=\frac{\mathrm{2}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \:{x}^{\mathrm{2}} {sin}\left({nx}\right){dx}\:\:\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{2}}{a}_{{n}} =\int_{\mathrm{0}} ^{\pi} \:{x}^{\mathrm{2}} {sin}\left({nx}\right){dx}\:\:{by}\:{parts}\:{u}\:={x}^{\mathrm{2}} \:{and}\:{v}^{'} \:={sin}\left({nx}\right)\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{2}}{a}_{{n}} =\left[−\frac{{x}^{\mathrm{2}} }{{n}}{cos}\left({nx}\right)\right]_{\mathrm{0}} ^{\pi} \:−\int_{\mathrm{0}} ^{\pi} \:\:\left(\mathrm{2}{x}\right)\left(−\frac{\mathrm{1}}{{n}}\right){cos}\left({nx}\right){dx} \\ $$$$=−\frac{\pi^{\mathrm{2}} }{{n}}\left(−\mathrm{1}\right)^{{n}} \:\:+\frac{\mathrm{2}}{{n}}\:\int_{\mathrm{0}} ^{\pi} \:\:{x}\:{cos}\left({nx}\right){dx}\:{again}\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:{x}\:{cos}\left({nx}\right){dx}\:=\left[\frac{{x}}{{n}}{sin}\left({nx}\right)\right]_{\mathrm{0}} ^{\pi} \:−\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{1}}{{n}}{sin}\left({nx}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\pi} \:{sin}\left({nx}\right){dx}\:=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left[{cos}\left({nx}\right)\right]_{\mathrm{0}} ^{\pi} \:=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left(\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right)\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{2}}{a}_{{n}} =−\frac{\pi^{\mathrm{2}} }{{n}}\left(−\mathrm{1}\right)^{{n}} \:+\frac{\mathrm{2}}{{n}^{\mathrm{3}} }\:\left\{\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right\} \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\pi}\left\{−\frac{\pi^{\mathrm{2}} }{{n}}\left(−\mathrm{1}\right)^{{n}} \:+\frac{\mathrm{2}}{{n}^{\mathrm{3}} }\left\{\:\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right)\right\} \\ $$$$=−\mathrm{2}\pi\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:+\frac{\mathrm{4}}{\pi{n}^{\mathrm{3}} }\left\{\:\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right\}\:\Rightarrow \\ $$$${x}\mid{x}\mid\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left(−\mathrm{2}\pi\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:+\frac{\mathrm{4}}{\pi{n}^{\mathrm{3}} }\left\{\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right\}\right){sin}\left({nx}\right) \\ $$$$=−\mathrm{2}\pi\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}{sin}\left({nx}\right)\:+\frac{\mathrm{4}}{\pi}\:\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}}{{n}^{\mathrm{3}} }{sin}\left({nx}\right) \\ $$$$ \\ $$$$ \\ $$
