Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 65319 by hovea cw last updated on 28/Jul/19

Commented by mathmax by abdo last updated on 28/Jul/19

those integrals are solved see the platform.

$${those}\:{integrals}\:{are}\:{solved}\:\:{see}\:{the}\:{platform}. \\ $$

Commented by mathmax by abdo last updated on 30/Jul/19

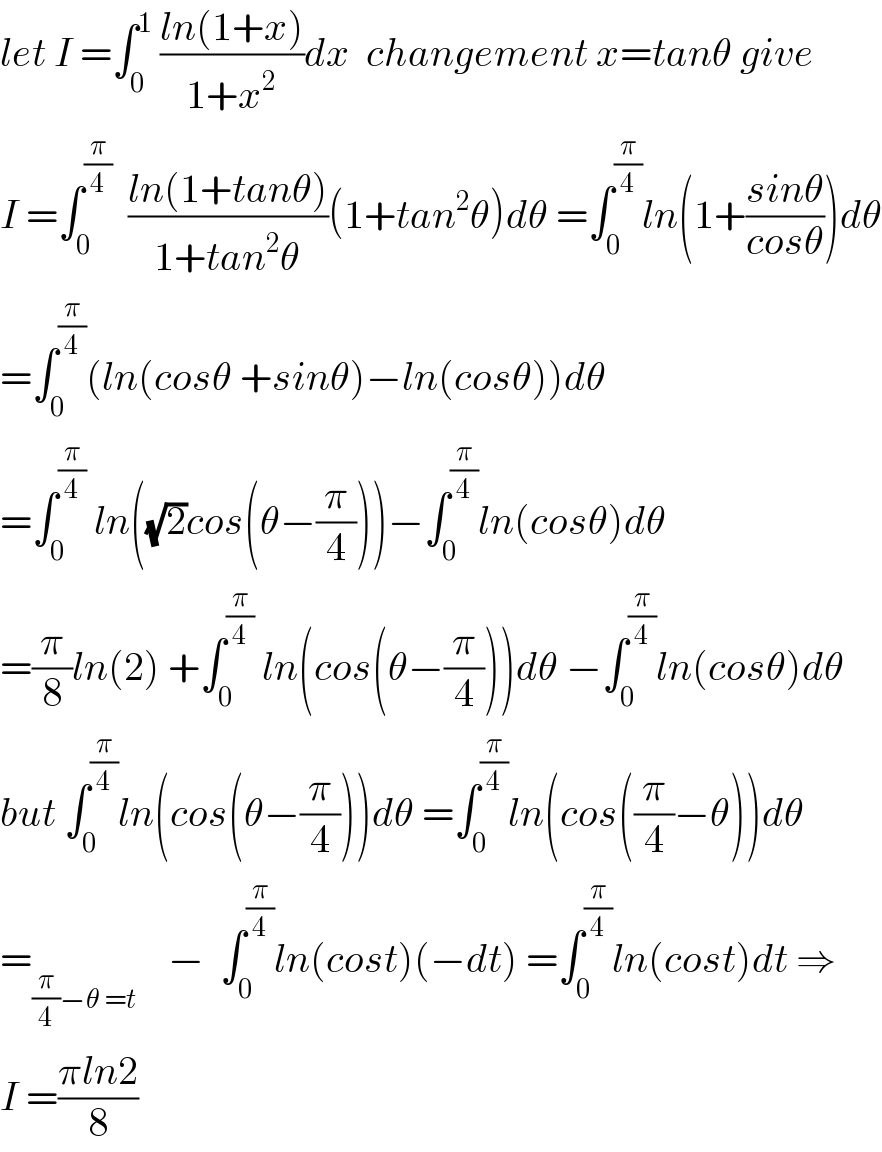
let I =∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx changement x=tanθ give I =∫_0 ^(π/4) ((ln(1+tanθ))/(1+tan^2 θ))(1+tan^2 θ)dθ =∫_0 ^(π/4) ln(1+((sinθ)/(cosθ)))dθ =∫_0 ^(π/4) (ln(cosθ +sinθ)−ln(cosθ))dθ =∫_0 ^(π/4) ln((√2)cos(θ−(π/4)))−∫_0 ^(π/4) ln(cosθ)dθ =(π/8)ln(2) +∫_0 ^(π/4) ln(cos(θ−(π/4)))dθ −∫_0 ^(π/4) ln(cosθ)dθ but ∫_0 ^(π/4) ln(cos(θ−(π/4)))dθ =∫_0 ^(π/4) ln(cos((π/4)−θ))dθ =_((π/4)−θ =t) − ∫_0 ^(π/4) ln(cost)(−dt) =∫_0 ^(π/4) ln(cost)dt ⇒ I =((πln2)/8)

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:{changement}\:{x}={tan}\theta\:{give}\: \\ $$$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{ln}\left(\mathrm{1}+{tan}\theta\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+\frac{{sin}\theta}{{cos}\theta}\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left({ln}\left({cos}\theta\:+{sin}\theta\right)−{ln}\left({cos}\theta\right)\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left(\sqrt{\mathrm{2}}{cos}\left(\theta−\frac{\pi}{\mathrm{4}}\right)\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\theta\right){d}\theta \\ $$$$=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left({cos}\left(\theta−\frac{\pi}{\mathrm{4}}\right)\right){d}\theta\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\theta\right){d}\theta \\ $$$${but}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\theta−\frac{\pi}{\mathrm{4}}\right)\right){d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\frac{\pi}{\mathrm{4}}−\theta\right)\right){d}\theta\:\:\:\:\: \\ $$$$=_{\frac{\pi}{\mathrm{4}}−\theta\:={t}} \:\:\:\:−\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cost}\right)\left(−{dt}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cost}\right){dt}\:\Rightarrow \\ $$$${I}\:=\frac{\pi{ln}\mathrm{2}}{\mathrm{8}} \\ $$

Answered by Tanmay chaudhury last updated on 28/Jul/19

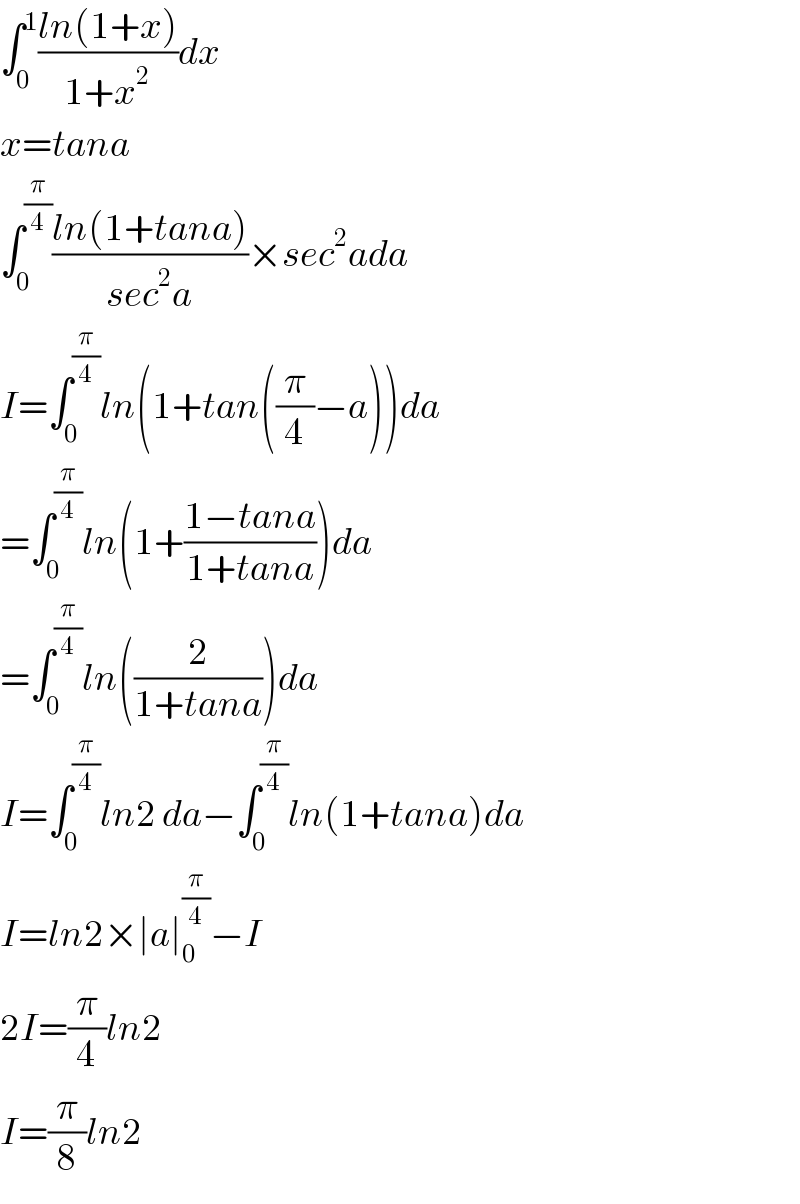
∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx x=tana ∫_0 ^(π/4) ((ln(1+tana))/(sec^2 a))×sec^2 ada I=∫_0 ^(π/4) ln(1+tan((π/4)−a))da =∫_0 ^(π/4) ln(1+((1−tana)/(1+tana)))da =∫_0 ^(π/4) ln((2/(1+tana)))da I=∫_0 ^(π/4) ln2 da−∫_0 ^(π/4) ln(1+tana)da I=ln2×∣a∣_0 ^(π/4) −I 2I=(π/4)ln2 I=(π/8)ln2

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${x}={tana} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{ln}\left(\mathrm{1}+{tana}\right)}{{sec}^{\mathrm{2}} {a}}×{sec}^{\mathrm{2}} {ada} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tan}\left(\frac{\pi}{\mathrm{4}}−{a}\right)\right){da} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}−{tana}}{\mathrm{1}+{tana}}\right){da} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{tana}}\right){da} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\mathrm{2}\:{da}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tana}\right){da} \\ $$$${I}={ln}\mathrm{2}×\mid{a}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} −{I} \\ $$$$\mathrm{2}{I}=\frac{\pi}{\mathrm{4}}{ln}\mathrm{2} \\ $$$${I}=\frac{\pi}{\mathrm{8}}{ln}\mathrm{2} \\ $$

Answered by Tanmay chaudhury last updated on 28/Jul/19

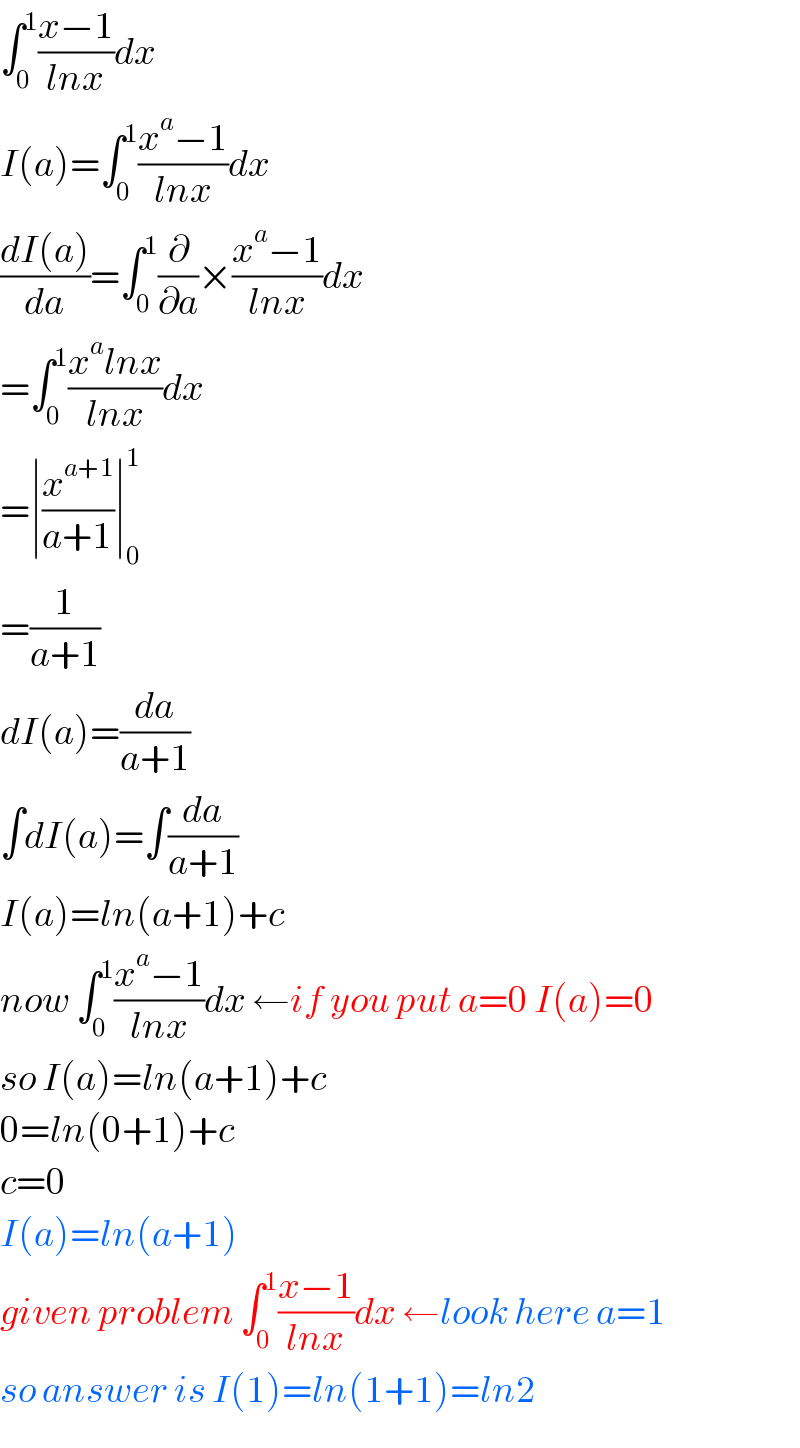
∫_0 ^1 ((x−1)/(lnx))dx I(a)=∫_0 ^1 ((x^a −1)/(lnx))dx ((dI(a))/da)=∫_0 ^1 (∂/∂a)×((x^a −1)/(lnx))dx =∫_0 ^1 ((x^a lnx)/(lnx))dx =∣(x^(a+1) /(a+1))∣_0 ^1 =(1/(a+1)) dI(a)=(da/(a+1)) ∫dI(a)=∫(da/(a+1)) I(a)=ln(a+1)+c now ∫_0 ^1 ((x^a −1)/(lnx))dx ←if you put a=0 I(a)=0 so I(a)=ln(a+1)+c 0=ln(0+1)+c c=0 I(a)=ln(a+1) given problem ∫_0 ^1 ((x−1)/(lnx))dx ←look here a=1 so answer is I(1)=ln(1+1)=ln2

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}}{{lnx}}{dx} \\ $$$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} −\mathrm{1}}{{lnx}}{dx} \\ $$$$\frac{{dI}\left({a}\right)}{{da}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\partial}{\partial{a}}×\frac{{x}^{{a}} −\mathrm{1}}{{lnx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} {lnx}}{{lnx}}{dx} \\ $$$$=\mid\frac{{x}^{{a}+\mathrm{1}} }{{a}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{a}+\mathrm{1}} \\ $$$${dI}\left({a}\right)=\frac{{da}}{{a}+\mathrm{1}} \\ $$$$\int{dI}\left({a}\right)=\int\frac{{da}}{{a}+\mathrm{1}} \\ $$$${I}\left({a}\right)={ln}\left({a}+\mathrm{1}\right)+{c} \\ $$$${now}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} −\mathrm{1}}{{lnx}}{dx}\:\leftarrow{if}\:{you}\:{put}\:{a}=\mathrm{0}\:{I}\left({a}\right)=\mathrm{0} \\ $$$${so}\:{I}\left({a}\right)={ln}\left({a}+\mathrm{1}\right)+{c} \\ $$$$\mathrm{0}={ln}\left(\mathrm{0}+\mathrm{1}\right)+{c} \\ $$$${c}=\mathrm{0} \\ $$$${I}\left({a}\right)={ln}\left({a}+\mathrm{1}\right) \\ $$$${given}\:{problem}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}}{{lnx}}{dx}\:\leftarrow{look}\:{here}\:{a}=\mathrm{1} \\ $$$${so}\:{answer}\:{is}\:{I}\left(\mathrm{1}\right)={ln}\left(\mathrm{1}+\mathrm{1}\right)={ln}\mathrm{2} \\ $$

Answered by Tanmay chaudhury last updated on 28/Jul/19

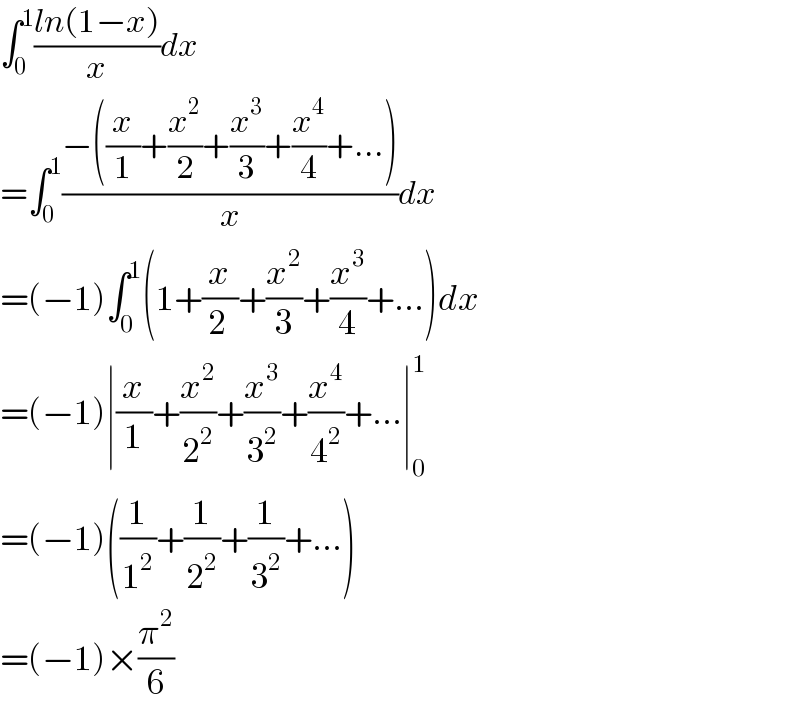
∫_0 ^1 ((ln(1−x))/x)dx =∫_0 ^1 ((−((x/1)+(x^2 /2)+(x^3 /3)+(x^4 /4)+...))/x)dx =(−1)∫_0 ^1 (1+(x/(2 ))+(x^2 /3)+(x^3 /4)+...)dx =(−1)∣(x/1)+(x^2 /2^2 )+(x^3 /3^2 )+(x^4 /4^2 )+...∣_0 ^1 =(−1)((1/1^2 )+(1/2^2 )+(1/3^2 )+...) =(−1)×(π^2 /6)

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\left(\frac{{x}}{\mathrm{1}}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}+...\right)}{{x}}{dx} \\ $$$$=\left(−\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{{x}}{\mathrm{2}\:}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+\frac{{x}^{\mathrm{3}} }{\mathrm{4}}+...\right){dx} \\ $$$$=\left(−\mathrm{1}\right)\mid\frac{{x}}{\mathrm{1}}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }+\frac{{x}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{2}} }+\frac{{x}^{\mathrm{4}} }{\mathrm{4}^{\mathrm{2}} }+...\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\left(−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...\right) \\ $$$$=\left(−\mathrm{1}\right)×\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com