
Question Number 65320 by hovea cw last updated on 28/Jul/19
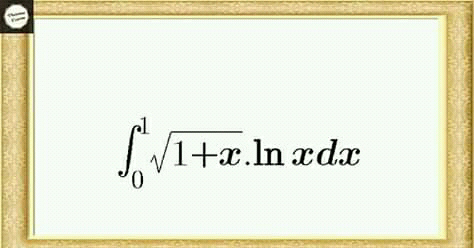
Commented by mathmax by abdo last updated on 28/Jul/19
![let I =∫_0 ^1 (√(1+x))lnxdx changement (√(1+x))=t give 1+x =t^2 ⇒ x =t^2 −1 and I =∫_1 ^(√2) tln(t^2 −1)(2t)dt =2 ∫_1 ^(√2) t^2 ln(t^2 −1)dt by parts u^′ =t^2 and v =ln(t^2 −1) ⇒ ∫_1 ^(√2) t^2 ln(t^2 −1)dt =[((t^3 /3)−(1/3))ln(t^2 −1)]_1 ^(√2) −∫_1 ^(√2) (((t^3 −1)/3))((2t)/(t^2 −1))dt =(((2(√2))/3)−(1/3))×0 −lim_(t→1) ((t^3 −1)/3)ln(t^2 −1)−(2/3) ∫_1 ^(√2) ((t^4 −t)/(t^2 −1))dt =0−0 −(2/3) ∫_1 ^(√2) ((t^4 −t)/(t^2 −1))dt ∫_1 ^(√2) ((t^4 −t)/(t^2 −1))dt =∫_1 ^(√2) ((t(t^3 −1))/(t^2 −1))dt =∫_1 ^(√2) ((t(t−1)(t^2 +t+1))/((t−1)(t+1)))dt =∫_1 ^(√2) ((t^3 +t^2 +t)/(t+1)) dt =∫_1 ^(√2) ((t^2 (t+1)−t^2 +t^2 +t)/(t+1))dt =∫_1 ^(√2) t^(2 ) dt +∫_1 ^(√2) ((tdt)/(t+1)) =[(t^3 /3)]_1 ^(√2) +∫_1 ^(√2) (1−(1/(t+1)))dt =((2(√2))/3)−(1/3) +(√2)−1 −[ln∣t+1∣]_1 ^(√2) =(5/3)(√2)−(4/3) −ln(1+(√2))+ln(2) ⇒ I =−(4/3){(5/3)(√2)−(4/3) +ln((2/(1+(√2))))} I =−((20)/9)(√(2 )) +((16)/9) −(4/3)ln((2/(1+(√2))))](Q65337.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{x}}{lnxdx}\:{changement}\:\sqrt{\mathrm{1}+{x}}={t}\:{give}\:\mathrm{1}+{x}\:={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}\:={t}^{\mathrm{2}} −\mathrm{1}\:\:{and}\:{I}\:=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} {tln}\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} {t}^{\mathrm{2}} {ln}\left({t}^{\mathrm{2}} −\mathrm{1}\right){dt}\:\:\:{by}\:{parts}\:{u}^{'} \:={t}^{\mathrm{2}} \:{and}\:{v}\:={ln}\left({t}^{\mathrm{2}} −\mathrm{1}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} {t}^{\mathrm{2}} {ln}\left({t}^{\mathrm{2}} −\mathrm{1}\right){dt}\:=\left[\left(\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\right){ln}\left({t}^{\mathrm{2}} −\mathrm{1}\right)\right]_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:−\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \left(\frac{{t}^{\mathrm{3}} −\mathrm{1}}{\mathrm{3}}\right)\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$$=\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\right)×\mathrm{0}\:−{lim}_{{t}\rightarrow\mathrm{1}} \frac{{t}^{\mathrm{3}} −\mathrm{1}}{\mathrm{3}}{ln}\left({t}^{\mathrm{2}} −\mathrm{1}\right)−\frac{\mathrm{2}}{\mathrm{3}}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\frac{{t}^{\mathrm{4}} −{t}}{{t}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$$=\mathrm{0}−\mathrm{0}\:−\frac{\mathrm{2}}{\mathrm{3}}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\frac{{t}^{\mathrm{4}} −{t}}{{t}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\frac{{t}^{\mathrm{4}} −{t}}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\:=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{t}\left({t}^{\mathrm{3}} −\mathrm{1}\right)}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\:=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\frac{{t}\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+{t}+\mathrm{1}\right)}{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{dt} \\ $$$$=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{t}^{\mathrm{3}} \:+{t}^{\mathrm{2}} \:+{t}}{{t}+\mathrm{1}}\:{dt}\:=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\frac{{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)−{t}^{\mathrm{2}} \:+{t}^{\mathrm{2}} \:+{t}}{{t}+\mathrm{1}}{dt} \\ $$$$=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:{t}^{\mathrm{2}\:} {dt}\:\:+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\frac{{tdt}}{{t}+\mathrm{1}}\:=\left[\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \left(\mathrm{1}−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\:+\sqrt{\mathrm{2}}−\mathrm{1}\:−\left[{ln}\mid{t}+\mathrm{1}\mid\right]_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:=\frac{\mathrm{5}}{\mathrm{3}}\sqrt{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{3}}\:−{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{4}}{\mathrm{3}}\left\{\frac{\mathrm{5}}{\mathrm{3}}\sqrt{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{3}}\:+{ln}\left(\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)\right\} \\ $$$${I}\:=−\frac{\mathrm{20}}{\mathrm{9}}\sqrt{\mathrm{2}\:}\:+\frac{\mathrm{16}}{\mathrm{9}}\:−\frac{\mathrm{4}}{\mathrm{3}}{ln}\left(\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right) \\ $$
