Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 6535 by Temp last updated on 01/Jul/16

Σ_(x=1) ^∞ (1/x) = 1+(1/2)+(1/3)+(1/4)+(1/5)+... Is the following true? ∴Σ(1/x)=Σ((1/(2x))+(1/(2x−1))) =Σ(((2x−1+2x)/(2x(2x−1)))) =Σ(((2x−2+1+2x)/(2x(2x−1)))) =Σ(((4x−2)/(2x(2x−1)))+(1/(2x(2x−1)))) =Σ(((2(2x−1))/(2x(2x−1)))+(1/(2x(2x−1)))) =Σ((1/x)+(1/(2x(2x−1)))) ∴ Σ_(x=1) ^∞ (1/x) =Σ_(x=1) ^∞ (1/x) +Σ_(x=1) ^∞ (1/(2x(2x−1)))

$$\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{x}}\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+... \\ $$$$\boldsymbol{\mathrm{Is}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{following}}\:\boldsymbol{\mathrm{true}}? \\ $$$$\therefore\Sigma\frac{\mathrm{1}}{{x}}=\Sigma\left(\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}}\right) \\ $$$$=\Sigma\left(\frac{\mathrm{2}{x}−\mathrm{1}+\mathrm{2}{x}}{\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{1}\right)}\right) \\ $$$$=\Sigma\left(\frac{\mathrm{2}{x}−\mathrm{2}+\mathrm{1}+\mathrm{2}{x}}{\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{1}\right)}\right) \\ $$$$=\Sigma\left(\frac{\mathrm{4}{x}−\mathrm{2}}{\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{1}\right)}\right) \\ $$$$=\Sigma\left(\frac{\mathrm{2}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{1}\right)}\right) \\ $$$$=\Sigma\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{1}\right)}\right) \\ $$$$\therefore\:\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{x}}\:=\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{x}}\:+\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{1}\right)} \\ $$

Commented by Temp last updated on 01/Jul/16

Note: Σ_(x=1) ^∞ (1/(2x(2x−1)))=Σ_(x=1) ^∞ ((1/(2x−1))−(1/(2x))) Σ_(x=1) ^∞ ((1/(2x−1))−(1/(2x)))=((1/1)−(1/2))+((1/3)−(1/4))+... Σ_(x=1) ^∞ ((1/(2x−1))−(1/(2x)))=1−(1/2)+(1/3)−(1/4)+(1/5)−(1/6)+... =ln(2) ∴ Σ_(x=1) ^∞ (1/x) = Σ_(x=1) ^∞ (1/x) + ln(2) How can this be true?

$$\boldsymbol{\mathrm{Note}}: \\ $$$$\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{1}\right)}=\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{x}}\right) \\ $$$$\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{x}}\right)=\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}\right)+... \\ $$$$\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{x}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{6}}+... \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\therefore\:\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{x}}\:=\:\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{x}}\:+\:\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{How}\:\mathrm{can}\:\mathrm{this}\:\mathrm{be}\:\mathrm{true}? \\ $$

Commented by prakash jain last updated on 01/Jul/16

Σ(1/n) is divergent hence splitting& rearrangmnts are not valid.

$$\Sigma\frac{\mathrm{1}}{{n}}\:\mathrm{is}\:\mathrm{divergent}\:\mathrm{hence}\:\mathrm{splitting\&}\:\mathrm{rearrangmnts} \\ $$$$\mathrm{are}\:\mathrm{not}\:\mathrm{valid}. \\ $$

Commented by prakash jain last updated on 01/Jul/16

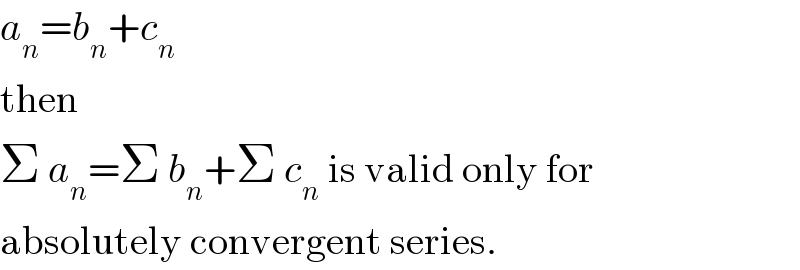
a_n =b_n +c_n then Σ a_n =Σ b_n +Σ c_n is valid only for absolutely convergent series.

$${a}_{{n}} ={b}_{{n}} +{c}_{{n}} \\ $$$$\mathrm{then} \\ $$$$\Sigma\:{a}_{{n}} =\Sigma\:{b}_{{n}} +\Sigma\:{c}_{{n}} \:\mathrm{is}\:\mathrm{valid}\:\mathrm{only}\:\mathrm{for} \\ $$$$\mathrm{absolutely}\:\mathrm{convergent}\:\mathrm{series}. \\ $$

Commented by Temp last updated on 02/Jul/16

I am not certain this is completely incorrect. If you solve both sides: ∞=∞+ln(2) True Although ∞−∞≠0 ∴ln(2)≠0

$$\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{certain}\:\mathrm{this}\:\mathrm{is}\:\mathrm{completely}\:\mathrm{incorrect}. \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{solve}\:\mathrm{both}\:\mathrm{sides}: \\ $$$$\infty=\infty+\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{True} \\ $$$$ \\ $$$$\mathrm{Although} \\ $$$$\infty−\infty\neq\mathrm{0} \\ $$$$\therefore\mathrm{ln}\left(\mathrm{2}\right)\neq\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com