Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 65367 by ajfour last updated on 29/Jul/19

Commented by ajfour last updated on 29/Jul/19

For maximum arc length of an origin centered circle within the shown unit circle, what is the radius of the circle.

$$\mathrm{For}\:\mathrm{maximum}\:\mathrm{arc}\:\mathrm{length}\:\mathrm{of}\:\mathrm{an} \\ $$$$\mathrm{origin}\:\mathrm{centered}\:\mathrm{circle}\:\mathrm{within} \\ $$$$\mathrm{the}\:\mathrm{shown}\:\mathrm{unit}\:\mathrm{circle},\:\mathrm{what}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}. \\ $$

Answered by ajfour last updated on 29/Jul/19

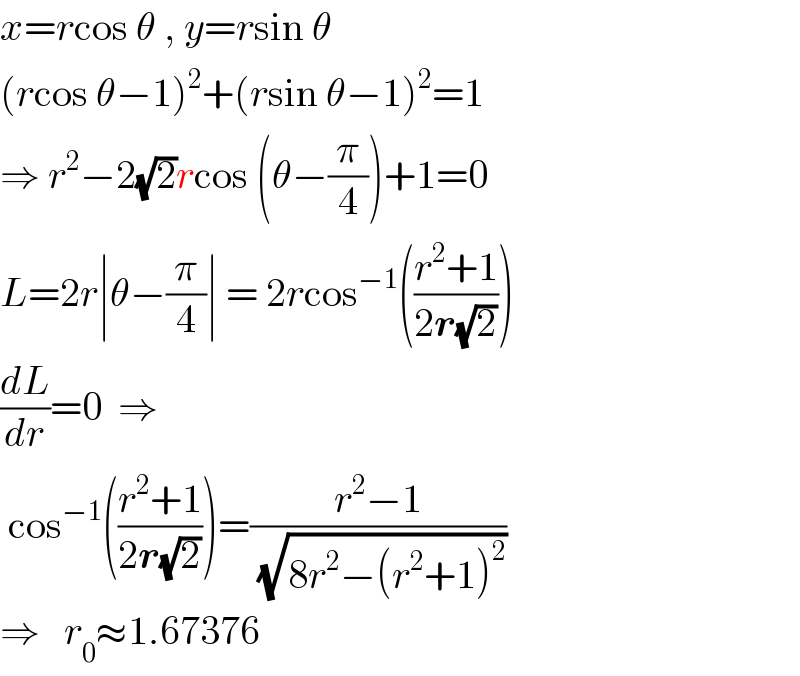
x=rcos θ , y=rsin θ (rcos θ−1)^2 +(rsin θ−1)^2 =1 ⇒ r^2 −2(√2)rcos (θ−(π/4))+1=0 L=2r∣θ−(π/4)∣ = 2rcos^(−1) (((r^2 +1)/(2r(√2)))) (dL/dr)=0 ⇒ cos^(−1) (((r^2 +1)/(2r(√2))))=((r^2 −1)/(√(8r^2 −(r^2 +1)^2 ))) ⇒ r_0 ≈1.67376

$${x}={r}\mathrm{cos}\:\theta\:,\:{y}={r}\mathrm{sin}\:\theta \\ $$$$\left({r}\mathrm{cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} +\left({r}\mathrm{sin}\:\theta−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{r}\mathrm{cos}\:\left(\theta−\frac{\pi}{\mathrm{4}}\right)+\mathrm{1}=\mathrm{0} \\ $$$${L}=\mathrm{2}{r}\mid\theta−\frac{\pi}{\mathrm{4}}\mid\:=\:\mathrm{2}{r}\mathrm{cos}^{−\mathrm{1}} \left(\frac{{r}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}\boldsymbol{{r}}\sqrt{\mathrm{2}}}\right) \\ $$$$\frac{{dL}}{{dr}}=\mathrm{0}\:\:\Rightarrow \\ $$$$\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{{r}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}\boldsymbol{{r}}\sqrt{\mathrm{2}}}\right)=\frac{{r}^{\mathrm{2}} −\mathrm{1}}{\sqrt{\mathrm{8}{r}^{\mathrm{2}} −\left({r}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\:\:{r}_{\mathrm{0}} \approx\mathrm{1}.\mathrm{67376} \\ $$

Answered by mr W last updated on 29/Jul/19

lower intersection point P: x_P =r cos α y_P =r sin α (r cos α−1)^2 +(r sin α−1)^2 =1 r^2 −2r(cos α+sin α)+1=0 ⇒cos α+sin α=((r^2 +1)/(2r)) ⇒sin 2α=(((r^2 +1)/(2r)))^2 −1=(((r^2 −1)/(2r)))^2 =cos ((π/2)−2α) ⇒(π/2)−2α=cos^(−1) (((r^2 −1)/(2r)))^2 L=r((π/2)−2α)=r cos^(−1) (((r^2 −1)/(2r)))^2 (dL/dr)=cos^(−1) (((r^2 −1)/(2r)))^2 −((r^4 −1)/(2r^2 (√(1−(((r^2 −1)/(2r)))^4 ))))=0 ⇒cos^(−1) (((r^2 −1)/(2r)))^2 =((r^4 −1)/(2r^2 (√(1−(((r^2 −1)/(2r)))^4 )))) ⇒r=1.6738 ⇒L_(max) =2.1374

$${lower}\:{intersection}\:{point}\:{P}: \\ $$$${x}_{{P}} ={r}\:\mathrm{cos}\:\alpha \\ $$$${y}_{{P}} ={r}\:\mathrm{sin}\:\alpha \\ $$$$\left({r}\:\mathrm{cos}\:\alpha−\mathrm{1}\right)^{\mathrm{2}} +\left({r}\:\mathrm{sin}\:\alpha−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{r}\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right)+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha=\frac{{r}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{r}} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}\alpha=\left(\frac{{r}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{r}}\right)^{\mathrm{2}} −\mathrm{1}=\left(\frac{{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{r}}\right)^{\mathrm{2}} =\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}\alpha\right) \\ $$$$\Rightarrow\frac{\pi}{\mathrm{2}}−\mathrm{2}\alpha=\mathrm{cos}^{−\mathrm{1}} \left(\frac{{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{r}}\right)^{\mathrm{2}} \\ $$$${L}={r}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}\alpha\right)={r}\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{r}}\right)^{\mathrm{2}} \\ $$$$\frac{{dL}}{{dr}}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{r}}\right)^{\mathrm{2}} −\frac{{r}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}{r}^{\mathrm{2}} \sqrt{\mathrm{1}−\left(\frac{{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{r}}\right)^{\mathrm{4}} }}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}^{−\mathrm{1}} \left(\frac{{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{r}}\right)^{\mathrm{2}} =\frac{{r}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}{r}^{\mathrm{2}} \sqrt{\mathrm{1}−\left(\frac{{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{r}}\right)^{\mathrm{4}} }} \\ $$$$\Rightarrow{r}=\mathrm{1}.\mathrm{6738} \\ $$$$\Rightarrow{L}_{{max}} =\mathrm{2}.\mathrm{1374} \\ $$

Commented by ajfour last updated on 29/Jul/19

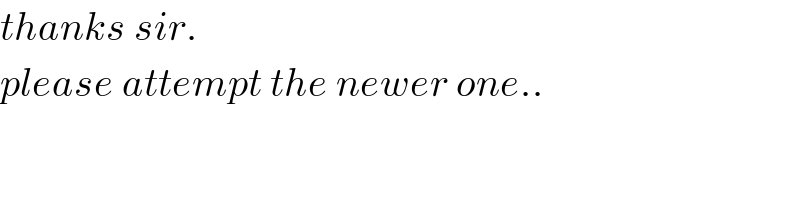
thanks sir. please attempt the newer one..

$${thanks}\:{sir}. \\ $$$${please}\:{attempt}\:{the}\:{newer}\:{one}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com