
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 65383 by mathmax by abdo last updated on 29/Jul/19
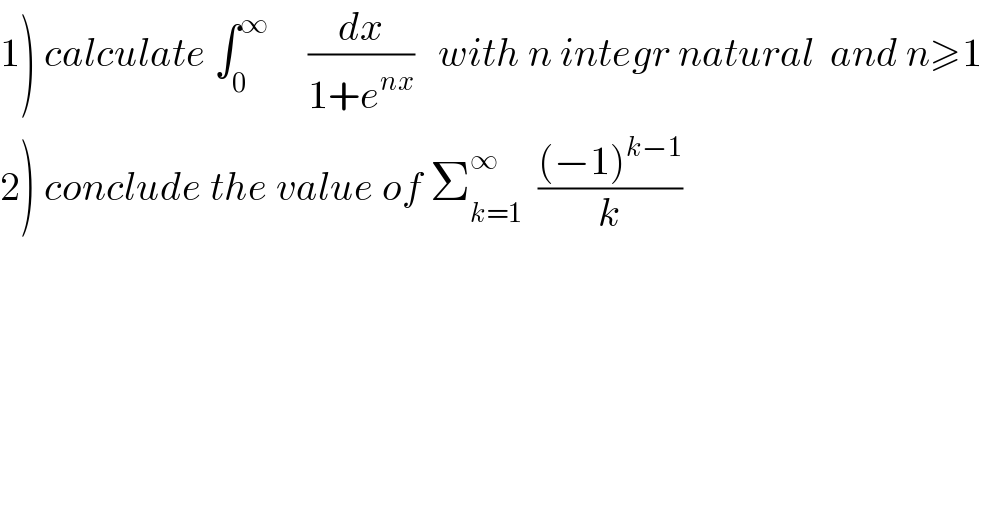
Commented by mathmax by abdo last updated on 30/Jul/19
![1) let A_n =∫_0 ^∞ (dx/(1+e^(nx) )) changement e^(nx) =t vive nx =lnt ⇒ A_n =∫_1 ^(+∞) (dt/(nt(1+t))) =(1/n)∫_1 ^(+∞) {(1/t)−(1/(t+1))}dt =(1/n)[ln∣(t/(t+1))∣]_1 ^(+∞) =(1/n){−ln((1/2))} =((ln(2))/n) 2) we have A_n =∫_0 ^∞ (dx/(1+e^(nx) )) =∫_0 ^∞ (e^(−nx) /(1+e^(−nx) ))dx =∫_0 ^∞ e^(−nx) {Σ_(k=0) ^∞ (−1)^k e^(−knx) } =Σ_(k=0) ^∞ (−1)^k ∫_0 ^∞ e^(−(n+kn)x) dx =Σ_(k=0) ^∞ (−1)^k [−(1/(n(k+1)))e^(−(n+kn)x) ]_0 ^(+∞) =(1/n)Σ_(k=0) ^∞ (((−1)^k )/(k+1)) =(1/n) Σ_(k=1) ^∞ (((−1)^(k−1) )/k) but A_n =((ln(2))/n) ⇒Σ_(k=1) ^∞ (((−1)^(k−1) )/k) =ln(2).](Q65467.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 65383 by mathmax by abdo last updated on 29/Jul/19 | ||
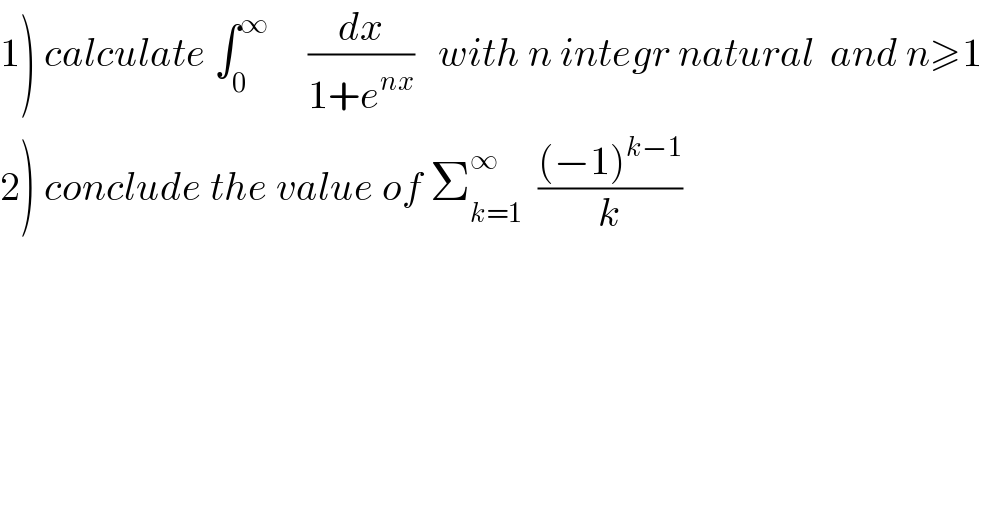 | ||
Commented by mathmax by abdo last updated on 30/Jul/19 | ||
![1) let A_n =∫_0 ^∞ (dx/(1+e^(nx) )) changement e^(nx) =t vive nx =lnt ⇒ A_n =∫_1 ^(+∞) (dt/(nt(1+t))) =(1/n)∫_1 ^(+∞) {(1/t)−(1/(t+1))}dt =(1/n)[ln∣(t/(t+1))∣]_1 ^(+∞) =(1/n){−ln((1/2))} =((ln(2))/n) 2) we have A_n =∫_0 ^∞ (dx/(1+e^(nx) )) =∫_0 ^∞ (e^(−nx) /(1+e^(−nx) ))dx =∫_0 ^∞ e^(−nx) {Σ_(k=0) ^∞ (−1)^k e^(−knx) } =Σ_(k=0) ^∞ (−1)^k ∫_0 ^∞ e^(−(n+kn)x) dx =Σ_(k=0) ^∞ (−1)^k [−(1/(n(k+1)))e^(−(n+kn)x) ]_0 ^(+∞) =(1/n)Σ_(k=0) ^∞ (((−1)^k )/(k+1)) =(1/n) Σ_(k=1) ^∞ (((−1)^(k−1) )/k) but A_n =((ln(2))/n) ⇒Σ_(k=1) ^∞ (((−1)^(k−1) )/k) =ln(2).](Q65467.png) | ||