
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 65386 by mathmax by abdo last updated on 29/Jul/19
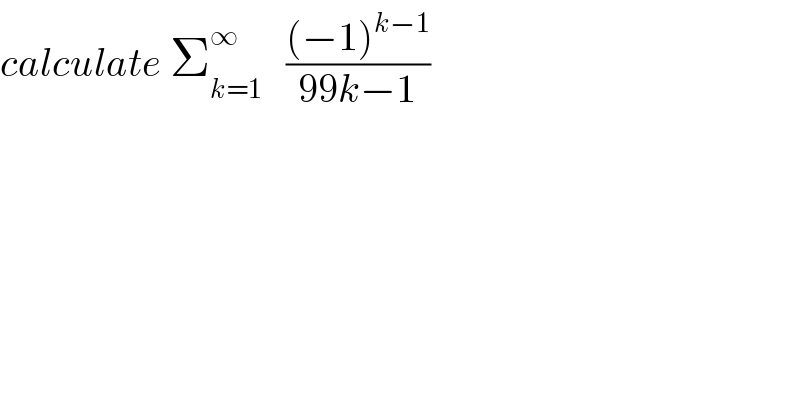
Commented by mathmax by abdo last updated on 31/Jul/19
![let I =∫_1 ^(+∞) (dx/(1+x^(99) )) cha7gement x=(1/t) give I =−∫_0 ^1 (1/(1+(1/t^(99) )))(−(dt/t^2 )) = ∫_0 ^1 (t^(99) /(t^2 (1+t^(99) )))dt =∫_0 ^1 (t^(97) /(1+t^(99) ))dt =∫_0 ^1 t^(97) Σ_(k=0) ^∞ (−1)^k t^(99k) dt = Σ_(k=0) ^∞ (−1)^k ∫_0 ^1 t^(99k+97) dt =Σ_(k=0) ^∞ (−1)^k [(1/(99k+98)) t^(99k+98) ]_0 ^1 =Σ_(k=0) ^∞ (((−1)^k )/(99k+98)) =_(k=p−1) Σ_(p=1) ^∞ (((−1)^(p−1) )/(99(p−1)+98)) =Σ_(p=1) ^∞ (((−1)^(p−1) )/(99p−1)) ⇒ Σ_(k=1) ^∞ (((−1)^(k−1) )/(99k−1)) =∫_1 ^(+∞) (dx/(1+x^(99) )) ∫_1 ^(+∞) (dx/(1+x^(99) )) =∫_1 ^0 (....)dx +∫_0 ^∞ (dx/(1+x^(99) )) =∫_0 ^∞ (dx/(1+x^(99) ))−∫_0 ^1 (dx/(1+x^(99) )) changement x =t^(1/(99)) give ∫_0 ^∞ (dx/(1+x^(99) )) =∫_0 ^∞ (1/(1+t))(1/(99))t^((1/(99))−1) dt =(1/(99))∫_0 ^∞ (t^((1/(99))−1) /(1+t))dt =(1/(99)) (π/(sin((π/(99))))) =(π/(99sin((π/(99))))) ∫_0 ^1 (dx/(1+x^(99) )) =∫_0 ^1 Σ_(n=0) ^∞ (−1)^n x^(99n) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(99n) dx =Σ_(n=0) ^∞ (−1)^(n ) [(1/(99n+1)) x^(99n+1) ]_0 ^1 =Σ_(n=0) ^∞ (((−1)^n )/(99n+1))=S =1−(1/(100)) +(1/(199)) −(1/(3.99+1)) +....⇒ Σ_(k=1) ^∞ (((−1)^(k−1) )/(99k−1)) =(π/(99sin((π/(99))))) −S](Q65584.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 65386 by mathmax by abdo last updated on 29/Jul/19 | ||
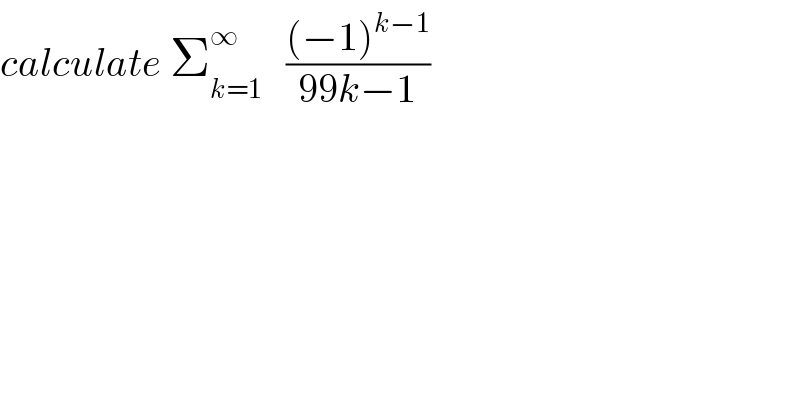 | ||
Commented by mathmax by abdo last updated on 31/Jul/19 | ||
![let I =∫_1 ^(+∞) (dx/(1+x^(99) )) cha7gement x=(1/t) give I =−∫_0 ^1 (1/(1+(1/t^(99) )))(−(dt/t^2 )) = ∫_0 ^1 (t^(99) /(t^2 (1+t^(99) )))dt =∫_0 ^1 (t^(97) /(1+t^(99) ))dt =∫_0 ^1 t^(97) Σ_(k=0) ^∞ (−1)^k t^(99k) dt = Σ_(k=0) ^∞ (−1)^k ∫_0 ^1 t^(99k+97) dt =Σ_(k=0) ^∞ (−1)^k [(1/(99k+98)) t^(99k+98) ]_0 ^1 =Σ_(k=0) ^∞ (((−1)^k )/(99k+98)) =_(k=p−1) Σ_(p=1) ^∞ (((−1)^(p−1) )/(99(p−1)+98)) =Σ_(p=1) ^∞ (((−1)^(p−1) )/(99p−1)) ⇒ Σ_(k=1) ^∞ (((−1)^(k−1) )/(99k−1)) =∫_1 ^(+∞) (dx/(1+x^(99) )) ∫_1 ^(+∞) (dx/(1+x^(99) )) =∫_1 ^0 (....)dx +∫_0 ^∞ (dx/(1+x^(99) )) =∫_0 ^∞ (dx/(1+x^(99) ))−∫_0 ^1 (dx/(1+x^(99) )) changement x =t^(1/(99)) give ∫_0 ^∞ (dx/(1+x^(99) )) =∫_0 ^∞ (1/(1+t))(1/(99))t^((1/(99))−1) dt =(1/(99))∫_0 ^∞ (t^((1/(99))−1) /(1+t))dt =(1/(99)) (π/(sin((π/(99))))) =(π/(99sin((π/(99))))) ∫_0 ^1 (dx/(1+x^(99) )) =∫_0 ^1 Σ_(n=0) ^∞ (−1)^n x^(99n) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(99n) dx =Σ_(n=0) ^∞ (−1)^(n ) [(1/(99n+1)) x^(99n+1) ]_0 ^1 =Σ_(n=0) ^∞ (((−1)^n )/(99n+1))=S =1−(1/(100)) +(1/(199)) −(1/(3.99+1)) +....⇒ Σ_(k=1) ^∞ (((−1)^(k−1) )/(99k−1)) =(π/(99sin((π/(99))))) −S](Q65584.png) | ||