Prove that 1^3 + 2^3 + 3^3 + … + n^3 = (1+2+3+...+n)^2


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 65587 by naka3546 last updated on 31/Jul/19

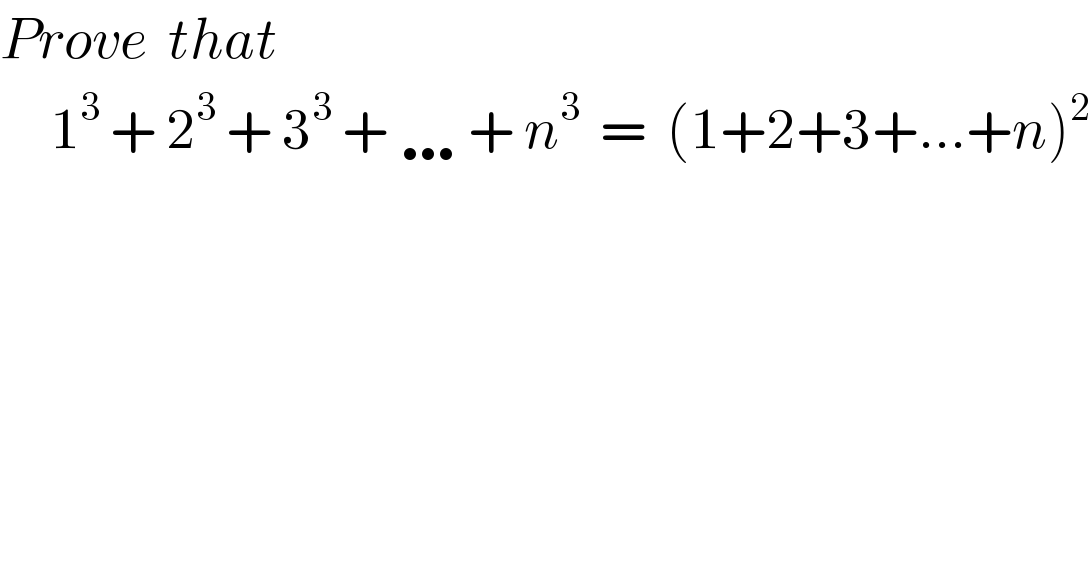
$${Prove}\:\:{that} \\ $$$$\:\:\:\:\:\mathrm{1}^{\mathrm{3}} \:+\:\mathrm{2}^{\mathrm{3}} \:+\:\mathrm{3}^{\mathrm{3}} \:+\:\ldots\:+\:{n}^{\mathrm{3}} \:\:=\:\:\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+...+{n}\right)^{\mathrm{2}} \\ $$
Commented by naka3546 last updated on 31/Jul/19

$${No}\:\:{using}\:\:{Mathematical}\:\:{Induction}\:. \\ $$
Commented by Tanmay chaudhury last updated on 31/Jul/19

Commented by Tanmay chaudhury last updated on 31/Jul/19
$S_3 =3∫S_2 dn+n×B_3 =3∫((n(n+1)(2n+1))/6)dn+n×0 =(1/2)∫n(2n^2 +3n+1)dn =(1/2)∫(2n^3 +3n^2 +n) dn (1/2)(((2n^4 )/4)+((3n^3 )/3)+(n^2 /2)) (1/2)(((6n^4 +12n^3 +6n^2 )/(12))) (1/4)(n^4 +2n^3 +n^2 ) (n^2 /4)(n^2 +2n+1) {((n(n+1))/2)}^2 Answer$
$${S}_{\mathrm{3}} =\mathrm{3}\int{S}_{\mathrm{2}} {dn}+{n}×{B}_{\mathrm{3}} \\ $$$$=\mathrm{3}\int\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}{dn}+{n}×\mathrm{0} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{n}\left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{1}\right){dn} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{2}{n}^{\mathrm{3}} +\mathrm{3}{n}^{\mathrm{2}} +{n}\right)\:\:{dn} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}{n}^{\mathrm{4}} }{\mathrm{4}}+\frac{\mathrm{3}{n}^{\mathrm{3}} }{\mathrm{3}}+\frac{{n}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{6}{n}^{\mathrm{4}} +\mathrm{12}{n}^{\mathrm{3}} +\mathrm{6}{n}^{\mathrm{2}} }{\mathrm{12}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left({n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +{n}^{\mathrm{2}} \right) \\ $$$$\frac{{n}^{\mathrm{2}} }{\mathrm{4}}\left({n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$\left\{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right\}^{\mathrm{2}} {Answer} \\ $$
Commented by Tanmay chaudhury last updated on 31/Jul/19

	Answered by som(math1967) last updated on 31/Jul/19
	$let s=1^3 +2^3 +3^3 +....+n^3 now n^4 −(n−1)^4 =4n^3 −6n^2 +4n−1 ∴1^4 −0=4.1^3 −6.1^2 +4.1 −1 2^4 −1^4 =4.2^3 −6.2^2 +4.2−1 ......... n^4 −(n−1)^4 =4n^3 −6n^2 +4n−1 add n^4 =4.(1^3 +2^3 +.....n^3 )−6(1^2 +2^2 +...n^2 ) +4(1+2+..n)−1×n n^4 =4s−6×((n(n+1)(2n+1))/6) +4×((n(n+1))/2)−n 4s=n^4 +n(n+1)(2n+1) −2n(n+1)+n 4s=n(n^3 +1) +n(n+1)(2n+1−2) 4s=n(n+1)(n^2 −n+1)+n(n+1)(2n−1) 4s=n(n+1)(n^2 −n+1+2n−1) 4s=n(n+1)n(n+1) ∴s={((n(n+1))/2)}^2 ∴s=(1+2+3+.......n)^2$
	$${let}\:{s}=\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} +....+{n}^{\mathrm{3}} \\ $$$${now}\:{n}^{\mathrm{4}} −\left({n}−\mathrm{1}\right)^{\mathrm{4}} =\mathrm{4}{n}^{\mathrm{3}} −\mathrm{6}{n}^{\mathrm{2}} +\mathrm{4}{n}−\mathrm{1} \\ $$$$\therefore\mathrm{1}^{\mathrm{4}} −\mathrm{0}=\mathrm{4}.\mathrm{1}^{\mathrm{3}} −\mathrm{6}.\mathrm{1}^{\mathrm{2}} +\mathrm{4}.\mathrm{1}\:−\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{4}} −\mathrm{1}^{\mathrm{4}} =\mathrm{4}.\mathrm{2}^{\mathrm{3}} −\mathrm{6}.\mathrm{2}^{\mathrm{2}} +\mathrm{4}.\mathrm{2}−\mathrm{1} \\ $$$$......... \\ $$$${n}^{\mathrm{4}} −\left({n}−\mathrm{1}\right)^{\mathrm{4}} =\mathrm{4}{n}^{\mathrm{3}} −\mathrm{6}{n}^{\mathrm{2}} +\mathrm{4}{n}−\mathrm{1} \\ $$$${add} \\ $$$${n}^{\mathrm{4}} =\mathrm{4}.\left(\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +.....{n}^{\mathrm{3}} \right)−\mathrm{6}\left(\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +...{n}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{4}\left(\mathrm{1}+\mathrm{2}+..{n}\right)−\mathrm{1}×{n} \\ $$$${n}^{\mathrm{4}} =\mathrm{4}{s}−\mathrm{6}×\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\:+\mathrm{4}×\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}−{n} \\ $$$$\mathrm{4}{s}={n}^{\mathrm{4}} +{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\:−\mathrm{2}{n}\left({n}+\mathrm{1}\right)+{n} \\ $$$$\mathrm{4}{s}={n}\left({n}^{\mathrm{3}} +\mathrm{1}\right)\:+{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}−\mathrm{2}\right) \\ $$$$\mathrm{4}{s}={n}\left({n}+\mathrm{1}\right)\left({n}^{\mathrm{2}} −{n}+\mathrm{1}\right)+{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$$\mathrm{4}{s}={n}\left({n}+\mathrm{1}\right)\left({n}^{\mathrm{2}} −{n}+\mathrm{1}+\mathrm{2}{n}−\mathrm{1}\right) \\ $$$$\mathrm{4}{s}={n}\left({n}+\mathrm{1}\right){n}\left({n}+\mathrm{1}\right) \\ $$$$ \\ $$$$\therefore{s}=\left\{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right\}^{\mathrm{2}} \\ $$$$\therefore{s}=\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+.......{n}\right)^{\mathrm{2}} \\ $$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum