Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 65830 by ajfour last updated on 04/Aug/19

Commented by ajfour last updated on 04/Aug/19

x^4 +ax^3 +bx^2 +cx+d=0 let roots be −p,−q,−r,−s. Find p,q,r,s in terms of a,b,c,d. a,b,c,d ∈R.

$${x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0} \\ $$$${let}\:{roots}\:{be}\:−{p},−{q},−{r},−{s}. \\ $$$${Find}\:{p},{q},{r},{s}\:{in}\:{terms}\:{of}\:{a},{b},{c},{d}. \\ $$$${a},{b},{c},{d}\:\in\mathbb{R}. \\ $$

Commented by MJS last updated on 05/Aug/19

my method as I did before is putting −p=α−(√β) −q=α+(√β) −r=γ−(√δ) −s=γ+(√δ) which leads to α=−γ−(a/2) β=−γ^2 −(a/2)γ+((a^2 −4b)/8)+((a^3 −4ab+8c)/(8(4γ+a))) δ=−γ^2 −(a/2)γ+((a^2 −4b)/8)−((a^3 −4ab+8c)/(8(4γ+a))) γ^6 +((3a)/2)γ^5 +((3a^2 +2b)/4)γ^4 +((a(a^2 +4b))/8)γ^3 +((2a^2 b+ac+b^2 −4d)/(16))γ^2 +((a(ac+b^2 −4d))/(32))γ−((a^2 d−abc+c^2 )/(64))=0 γ=r−(a/4) r^6 −((3a^2 −8b)/(16))r^4 +((3a^4 −16a^2 b+16ac+16(b^2 −4d))/(256))r^2 −(((a^3 −4ab+8c)^2 )/(4096))=0 r=(√s) s^3 −((3a^2 −8b)/(16))s^2 +((3a^4 −16a^2 b+16ac+16(b^2 −4d))/(256))s−(((a^3 −4ab+8c)^2 )/(4096))=0 s=t+((3a^2 −8b)/(48)) t^3 +((3ac−b^2 −12d)/(48))t−((27a^2 d−9abc+2b^3 −72bd+27c^2 )/(1728))=0 and we can always solve this depending on D we need Cardano′s or the trigonometric method D=27a^4 d^2 −18a^3 bcd+4a^3 c^3 +4a^2 b^3 d−a^2 b^2 c^2 −144a^2 bd^2 +6a^2 c^2 d+80ab^2 cd−18abc^3 +192acd^2 −16b^4 d+4b^3 c^2 +128b^2 d^2 −144bc^2 d+27c^4 −256d^3

$$\mathrm{my}\:\mathrm{method}\:\mathrm{as}\:\mathrm{I}\:\mathrm{did}\:\mathrm{before}\:\mathrm{is}\:\mathrm{putting} \\ $$$$−{p}=\alpha−\sqrt{\beta} \\ $$$$−{q}=\alpha+\sqrt{\beta} \\ $$$$−{r}=\gamma−\sqrt{\delta} \\ $$$$−{s}=\gamma+\sqrt{\delta} \\ $$$$\mathrm{which}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\alpha=−\gamma−\frac{{a}}{\mathrm{2}} \\ $$$$\beta=−\gamma^{\mathrm{2}} −\frac{{a}}{\mathrm{2}}\gamma+\frac{{a}^{\mathrm{2}} −\mathrm{4}{b}}{\mathrm{8}}+\frac{{a}^{\mathrm{3}} −\mathrm{4}{ab}+\mathrm{8}{c}}{\mathrm{8}\left(\mathrm{4}\gamma+{a}\right)} \\ $$$$\delta=−\gamma^{\mathrm{2}} −\frac{{a}}{\mathrm{2}}\gamma+\frac{{a}^{\mathrm{2}} −\mathrm{4}{b}}{\mathrm{8}}−\frac{{a}^{\mathrm{3}} −\mathrm{4}{ab}+\mathrm{8}{c}}{\mathrm{8}\left(\mathrm{4}\gamma+{a}\right)} \\ $$$$\gamma^{\mathrm{6}} +\frac{\mathrm{3}{a}}{\mathrm{2}}\gamma^{\mathrm{5}} +\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}{b}}{\mathrm{4}}\gamma^{\mathrm{4}} +\frac{{a}\left({a}^{\mathrm{2}} +\mathrm{4}{b}\right)}{\mathrm{8}}\gamma^{\mathrm{3}} +\frac{\mathrm{2}{a}^{\mathrm{2}} {b}+{ac}+{b}^{\mathrm{2}} −\mathrm{4}{d}}{\mathrm{16}}\gamma^{\mathrm{2}} +\frac{{a}\left({ac}+{b}^{\mathrm{2}} −\mathrm{4}{d}\right)}{\mathrm{32}}\gamma−\frac{{a}^{\mathrm{2}} {d}−{abc}+{c}^{\mathrm{2}} }{\mathrm{64}}=\mathrm{0} \\ $$$$\gamma={r}−\frac{{a}}{\mathrm{4}} \\ $$$${r}^{\mathrm{6}} −\frac{\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{b}}{\mathrm{16}}{r}^{\mathrm{4}} +\frac{\mathrm{3}{a}^{\mathrm{4}} −\mathrm{16}{a}^{\mathrm{2}} {b}+\mathrm{16}{ac}+\mathrm{16}\left({b}^{\mathrm{2}} −\mathrm{4}{d}\right)}{\mathrm{256}}{r}^{\mathrm{2}} −\frac{\left({a}^{\mathrm{3}} −\mathrm{4}{ab}+\mathrm{8}{c}\right)^{\mathrm{2}} }{\mathrm{4096}}=\mathrm{0} \\ $$$${r}=\sqrt{{s}} \\ $$$${s}^{\mathrm{3}} −\frac{\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{b}}{\mathrm{16}}{s}^{\mathrm{2}} +\frac{\mathrm{3}{a}^{\mathrm{4}} −\mathrm{16}{a}^{\mathrm{2}} {b}+\mathrm{16}{ac}+\mathrm{16}\left({b}^{\mathrm{2}} −\mathrm{4}{d}\right)}{\mathrm{256}}{s}−\frac{\left({a}^{\mathrm{3}} −\mathrm{4}{ab}+\mathrm{8}{c}\right)^{\mathrm{2}} }{\mathrm{4096}}=\mathrm{0} \\ $$$${s}={t}+\frac{\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{b}}{\mathrm{48}} \\ $$$${t}^{\mathrm{3}} +\frac{\mathrm{3}{ac}−{b}^{\mathrm{2}} −\mathrm{12}{d}}{\mathrm{48}}{t}−\frac{\mathrm{27}{a}^{\mathrm{2}} {d}−\mathrm{9}{abc}+\mathrm{2}{b}^{\mathrm{3}} −\mathrm{72}{bd}+\mathrm{27}{c}^{\mathrm{2}} }{\mathrm{1728}}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{we}\:\mathrm{can}\:\mathrm{always}\:\mathrm{solve}\:\mathrm{this} \\ $$$$\mathrm{depending}\:\mathrm{on}\:{D}\:\mathrm{we}\:\mathrm{need}\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{or}\:\mathrm{the} \\ $$$$\mathrm{trigonometric}\:\mathrm{method} \\ $$$${D}=\mathrm{27}{a}^{\mathrm{4}} {d}^{\mathrm{2}} −\mathrm{18}{a}^{\mathrm{3}} {bcd}+\mathrm{4}{a}^{\mathrm{3}} {c}^{\mathrm{3}} +\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{3}} {d}−{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} −\mathrm{144}{a}^{\mathrm{2}} {bd}^{\mathrm{2}} +\mathrm{6}{a}^{\mathrm{2}} {c}^{\mathrm{2}} {d}+\mathrm{80}{ab}^{\mathrm{2}} {cd}−\mathrm{18}{abc}^{\mathrm{3}} +\mathrm{192}{acd}^{\mathrm{2}} −\mathrm{16}{b}^{\mathrm{4}} {d}+\mathrm{4}{b}^{\mathrm{3}} {c}^{\mathrm{2}} +\mathrm{128}{b}^{\mathrm{2}} {d}^{\mathrm{2}} −\mathrm{144}{bc}^{\mathrm{2}} {d}+\mathrm{27}{c}^{\mathrm{4}} −\mathrm{256}{d}^{\mathrm{3}} \\ $$

Commented by ajfour last updated on 05/Aug/19

my method is now simpler still; some calculation error lead me to disbelieve.

$${my}\:{method}\:{is}\:{now}\:{simpler}\:{still}; \\ $$$${some}\:{calculation}\:{error}\:{lead}\:{me} \\ $$$${to}\:{disbelieve}. \\ $$

Answered by ajfour last updated on 05/Aug/19

x^4 +ax^3 +bx^2 +cx+d=0 x=t−(a/4) t^4 +At^2 +Bt+C=0 t^2 −Pt+(1/2)(A+P^2 +(B/P))=0 ...(I) P^( 6) +2AP^( 4) +(A^2 −4C)P^( 2) −B^2 =0 Cardano′s or trigonometric sol^n provides for P^( 2) . D=(1/4)(((2A^3 )/(27))+B^2 −((8AC)/3))^2 −(1/(27))((A^2 /3)+4C)^3 Any value of P^( 2) provides all the four roots using eq.(I).

$${x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0} \\ $$$${x}={t}−\frac{{a}}{\mathrm{4}} \\ $$$${t}^{\mathrm{4}} +{At}^{\mathrm{2}} +{Bt}+{C}=\mathrm{0} \\ $$$${t}^{\mathrm{2}} −{Pt}+\frac{\mathrm{1}}{\mathrm{2}}\left({A}+{P}^{\mathrm{2}} +\frac{{B}}{{P}}\right)=\mathrm{0}\:\:\:\:...\left({I}\right) \\ $$$${P}^{\:\mathrm{6}} +\mathrm{2}{AP}^{\:\mathrm{4}} +\left({A}^{\mathrm{2}} −\mathrm{4}{C}\right){P}^{\:\mathrm{2}} −{B}^{\mathrm{2}} =\mathrm{0} \\ $$$${Cardano}'{s}\:{or}\:{trigonometric}\:{sol}^{{n}} \\ $$$${provides}\:{for}\:{P}^{\:\mathrm{2}} . \\ $$$${D}=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{2}{A}^{\mathrm{3}} }{\mathrm{27}}+{B}^{\mathrm{2}} −\frac{\mathrm{8}{AC}}{\mathrm{3}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{27}}\left(\frac{{A}^{\mathrm{2}} }{\mathrm{3}}+\mathrm{4}{C}\right)^{\mathrm{3}} \\ $$$${Any}\:{value}\:{of}\:{P}^{\:\mathrm{2}} \:{provides}\:{all}\:{the} \\ $$$${four}\:{roots}\:{using}\:{eq}.\left({I}\right). \\ $$

Commented by ajfour last updated on 05/Aug/19

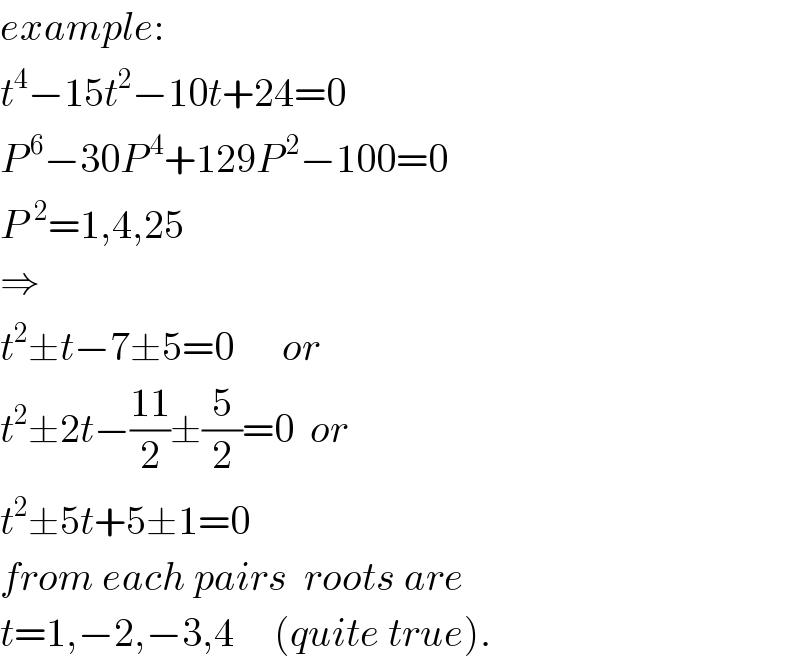
example: t^4 −15t^2 −10t+24=0 P^( 6) −30P^( 4) +129P^( 2) −100=0 P^2 =1,4,25 ⇒ t^2 ±t−7±5=0 or t^2 ±2t−((11)/2)±(5/2)=0 or t^2 ±5t+5±1=0 from each pairs roots are t=1,−2,−3,4 (quite true).

$${example}: \\ $$$${t}^{\mathrm{4}} −\mathrm{15}{t}^{\mathrm{2}} −\mathrm{10}{t}+\mathrm{24}=\mathrm{0} \\ $$$${P}^{\:\mathrm{6}} −\mathrm{30}{P}^{\:\mathrm{4}} +\mathrm{129}{P}^{\:\mathrm{2}} −\mathrm{100}=\mathrm{0} \\ $$$${P}\:^{\mathrm{2}} =\mathrm{1},\mathrm{4},\mathrm{25} \\ $$$$\Rightarrow \\ $$$${t}^{\mathrm{2}} \pm{t}−\mathrm{7}\pm\mathrm{5}=\mathrm{0}\:\:\:\:\:\:{or} \\ $$$${t}^{\mathrm{2}} \pm\mathrm{2}{t}−\frac{\mathrm{11}}{\mathrm{2}}\pm\frac{\mathrm{5}}{\mathrm{2}}=\mathrm{0}\:\:{or} \\ $$$${t}^{\mathrm{2}} \pm\mathrm{5}{t}+\mathrm{5}\pm\mathrm{1}=\mathrm{0} \\ $$$${from}\:{each}\:{pairs}\:\:{roots}\:{are} \\ $$$${t}=\mathrm{1},−\mathrm{2},−\mathrm{3},\mathrm{4}\:\:\:\:\:\left({quite}\:{true}\right). \\ $$

Commented by MJS last updated on 05/Aug/19

yes. but also p=−p are there 2 equations of the 6 possible for t which generally give the 4 solutions? can you determine which pairs of equations will do?

$$\mathrm{yes}. \\ $$$$\mathrm{but}\:\mathrm{also}\:{p}=−{p} \\ $$$$\mathrm{are}\:\mathrm{there}\:\mathrm{2}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{the}\:\mathrm{6}\:\mathrm{possible}\:\mathrm{for}\:{t} \\ $$$$\mathrm{which}\:\mathrm{generally}\:\mathrm{give}\:\mathrm{the}\:\mathrm{4}\:\mathrm{solutions}? \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{determine}\:\mathrm{which}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{equations} \\ $$$$\mathrm{will}\:\mathrm{do}? \\ $$

Commented by ajfour last updated on 05/Aug/19

[t^2 −Pt+(1/2)(A+P^( 2) +(B/P))][t^2 +Pt+(1/2)(A+P^( 2) −(B/P))]=0 we can choose just one value of P and use both equations, or P =±(√P^( 2) ) in any one of them, is that what you asked sir? its all the same, natural beauty!

$$\left[{t}^{\mathrm{2}} −{Pt}+\frac{\mathrm{1}}{\mathrm{2}}\left({A}+{P}^{\:\mathrm{2}} +\frac{{B}}{{P}}\right)\right]\left[{t}^{\mathrm{2}} +{Pt}+\frac{\mathrm{1}}{\mathrm{2}}\left({A}+{P}^{\:\mathrm{2}} −\frac{{B}}{{P}}\right)\right]=\mathrm{0} \\ $$$${we}\:{can}\:{choose}\:{just}\:{one}\:{value}\:{of} \\ $$$${P}\:{and}\:{use}\:{both}\:{equations},\:{or} \\ $$$${P}\:=\pm\sqrt{{P}^{\:\mathrm{2}} }\:\:{in}\:{any}\:{one}\:{of}\:{them}, \\ $$$${is}\:{that}\:{what}\:{you}\:{asked}\:{sir}? \\ $$$${its}\:{all}\:{the}\:{same},\:{natural}\:{beauty}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com