Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 65858 by ugwu Kingsley last updated on 05/Aug/19

Commented by mathmax by abdo last updated on 05/Aug/19

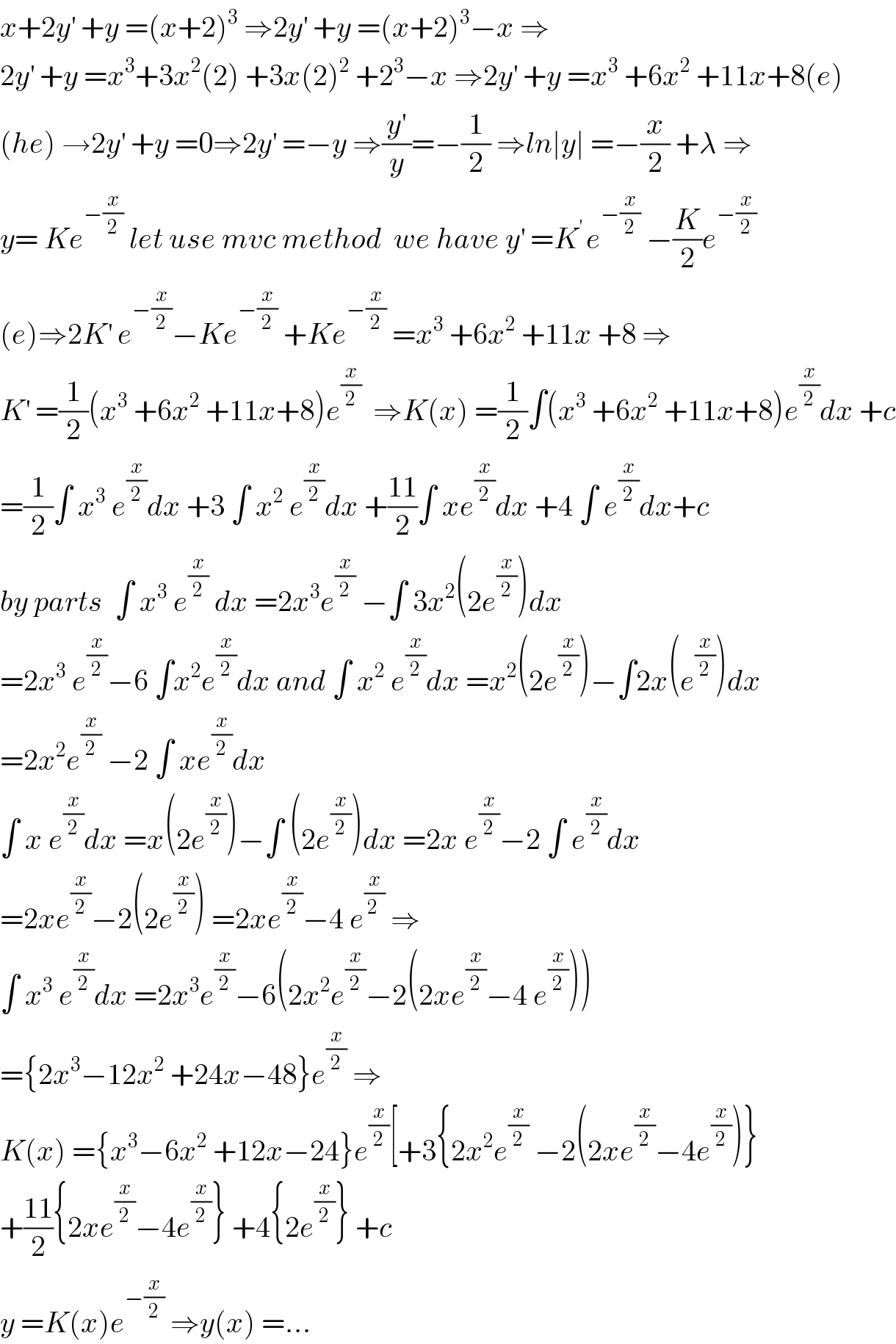
x+2y^′ +y =(x+2)^3 ⇒2y^′ +y =(x+2)^3 −x ⇒ 2y^′ +y =x^3 +3x^2 (2) +3x(2)^2 +2^3 −x ⇒2y^′ +y =x^3 +6x^2 +11x+8(e) (he) →2y^′ +y =0⇒2y^′ =−y ⇒(y^′ /y)=−(1/2) ⇒ln∣y∣ =−(x/2) +λ ⇒ y= Ke^(−(x/2)) let use mvc method we have y^′ =K^(′ ) e^(−(x/2)) −(K/2)e^(−(x/2)) (e)⇒2K^′ e^(−(x/2)) −Ke^(−(x/2)) +Ke^(−(x/2)) =x^3 +6x^2 +11x +8 ⇒ K^′ =(1/2)(x^3 +6x^2 +11x+8)e^(x/2) ⇒K(x) =(1/2)∫(x^3 +6x^2 +11x+8)e^(x/2) dx +c =(1/2)∫ x^3 e^(x/2) dx +3 ∫ x^2 e^(x/2) dx +((11)/2)∫ xe^(x/2) dx +4 ∫ e^(x/2) dx+c by parts ∫ x^3 e^(x/2) dx =2x^3 e^(x/2) −∫ 3x^2 (2e^(x/2) )dx =2x^3 e^(x/2) −6 ∫x^2 e^(x/2) dx and ∫ x^2 e^(x/2) dx =x^2 (2e^(x/2) )−∫2x(e^(x/2) )dx =2x^2 e^(x/2) −2 ∫ xe^(x/2) dx ∫ x e^(x/2) dx =x(2e^(x/2) )−∫ (2e^(x/2) )dx =2x e^(x/2) −2 ∫ e^(x/2) dx =2xe^(x/2) −2(2e^(x/2) ) =2xe^(x/2) −4 e^(x/(2 )) ⇒ ∫ x^3 e^(x/2) dx =2x^3 e^(x/2) −6(2x^2 e^(x/2) −2(2xe^(x/2) −4 e^(x/2) )) ={2x^3 −12x^2 +24x−48}e^(x/2) ⇒ K(x) ={x^3 −6x^2 +12x−24}e^(x/2) [+3{2x^2 e^(x/2) −2(2xe^(x/2) −4e^(x/2) )} +((11)/2){2xe^(x/2) −4e^(x/2) } +4{2e^(x/2) } +c y =K(x)e^(−(x/2)) ⇒y(x) =...

$${x}+\mathrm{2}{y}^{'} \:+{y}\:=\left({x}+\mathrm{2}\right)^{\mathrm{3}} \:\Rightarrow\mathrm{2}{y}^{'} \:+{y}\:=\left({x}+\mathrm{2}\right)^{\mathrm{3}} −{x}\:\Rightarrow \\ $$$$\mathrm{2}{y}^{'} \:+{y}\:={x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} \left(\mathrm{2}\right)\:+\mathrm{3}{x}\left(\mathrm{2}\right)^{\mathrm{2}} \:+\mathrm{2}^{\mathrm{3}} −{x}\:\Rightarrow\mathrm{2}{y}^{'} \:+{y}\:={x}^{\mathrm{3}} \:+\mathrm{6}{x}^{\mathrm{2}} \:+\mathrm{11}{x}+\mathrm{8}\left({e}\right) \\ $$$$\left({he}\right)\:\rightarrow\mathrm{2}{y}^{'} \:+{y}\:=\mathrm{0}\Rightarrow\mathrm{2}{y}^{'} \:=−{y}\:\Rightarrow\frac{{y}^{'} }{{y}}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{ln}\mid{y}\mid\:=−\frac{{x}}{\mathrm{2}}\:+\lambda\:\Rightarrow \\ $$$${y}=\:{Ke}^{−\frac{{x}}{\mathrm{2}}} \:{let}\:{use}\:{mvc}\:{method}\:\:{we}\:{have}\:{y}^{'} \:={K}^{'\:} {e}^{−\frac{{x}}{\mathrm{2}}} \:−\frac{{K}}{\mathrm{2}}{e}^{−\frac{{x}}{\mathrm{2}}} \\ $$$$\left({e}\right)\Rightarrow\mathrm{2}{K}^{'} \:{e}^{−\frac{{x}}{\mathrm{2}}} −{Ke}^{−\frac{{x}}{\mathrm{2}}} \:+{Ke}^{−\frac{{x}}{\mathrm{2}}} \:={x}^{\mathrm{3}} \:+\mathrm{6}{x}^{\mathrm{2}} \:+\mathrm{11}{x}\:+\mathrm{8}\:\Rightarrow \\ $$$${K}^{'} \:=\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{3}} \:+\mathrm{6}{x}^{\mathrm{2}} \:+\mathrm{11}{x}+\mathrm{8}\right){e}^{\frac{{x}}{\mathrm{2}}} \:\:\Rightarrow{K}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\int\left({x}^{\mathrm{3}} \:+\mathrm{6}{x}^{\mathrm{2}} \:+\mathrm{11}{x}+\mathrm{8}\right){e}^{\frac{{x}}{\mathrm{2}}} {dx}\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:{x}^{\mathrm{3}} \:{e}^{\frac{{x}}{\mathrm{2}}} {dx}\:+\mathrm{3}\:\int\:{x}^{\mathrm{2}} \:{e}^{\frac{{x}}{\mathrm{2}}} {dx}\:+\frac{\mathrm{11}}{\mathrm{2}}\int\:{xe}^{\frac{{x}}{\mathrm{2}}} {dx}\:+\mathrm{4}\:\int\:{e}^{\frac{{x}}{\mathrm{2}}} {dx}+{c} \\ $$$${by}\:{parts}\:\:\int\:{x}^{\mathrm{3}} \:{e}^{\frac{{x}}{\mathrm{2}}} \:{dx}\:=\mathrm{2}{x}^{\mathrm{3}} {e}^{\frac{{x}}{\mathrm{2}}} \:−\int\:\mathrm{3}{x}^{\mathrm{2}} \left(\mathrm{2}{e}^{\frac{{x}}{\mathrm{2}}} \right){dx} \\ $$$$=\mathrm{2}{x}^{\mathrm{3}} \:{e}^{\frac{{x}}{\mathrm{2}}} −\mathrm{6}\:\int{x}^{\mathrm{2}} {e}^{\frac{{x}}{\mathrm{2}}} {dx}\:{and}\:\int\:{x}^{\mathrm{2}} \:{e}^{\frac{{x}}{\mathrm{2}}} {dx}\:={x}^{\mathrm{2}} \left(\mathrm{2}{e}^{\frac{{x}}{\mathrm{2}}} \right)−\int\mathrm{2}{x}\left({e}^{\frac{{x}}{\mathrm{2}}} \right){dx} \\ $$$$=\mathrm{2}{x}^{\mathrm{2}} {e}^{\frac{{x}}{\mathrm{2}}} \:−\mathrm{2}\:\int\:{xe}^{\frac{{x}}{\mathrm{2}}} {dx} \\ $$$$\int\:{x}\:{e}^{\frac{{x}}{\mathrm{2}}} {dx}\:={x}\left(\mathrm{2}{e}^{\frac{{x}}{\mathrm{2}}} \right)−\int\:\left(\mathrm{2}{e}^{\frac{{x}}{\mathrm{2}}} \right){dx}\:=\mathrm{2}{x}\:{e}^{\frac{{x}}{\mathrm{2}}} −\mathrm{2}\:\int\:{e}^{\frac{{x}}{\mathrm{2}}} {dx} \\ $$$$=\mathrm{2}{xe}^{\frac{{x}}{\mathrm{2}}} −\mathrm{2}\left(\mathrm{2}{e}^{\frac{{x}}{\mathrm{2}}} \right)\:=\mathrm{2}{xe}^{\frac{{x}}{\mathrm{2}}} −\mathrm{4}\:{e}^{\frac{{x}}{\mathrm{2}\:}} \:\Rightarrow \\ $$$$\int\:{x}^{\mathrm{3}} \:{e}^{\frac{{x}}{\mathrm{2}}} {dx}\:=\mathrm{2}{x}^{\mathrm{3}} {e}^{\frac{{x}}{\mathrm{2}}} −\mathrm{6}\left(\mathrm{2}{x}^{\mathrm{2}} {e}^{\frac{{x}}{\mathrm{2}}} −\mathrm{2}\left(\mathrm{2}{xe}^{\frac{{x}}{\mathrm{2}}} −\mathrm{4}\:{e}^{\frac{{x}}{\mathrm{2}}} \right)\right) \\ $$$$=\left\{\mathrm{2}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} \:+\mathrm{24}{x}−\mathrm{48}\right\}{e}^{\frac{{x}}{\mathrm{2}}} \:\Rightarrow \\ $$$${K}\left({x}\right)\:=\left\{{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} \:+\mathrm{12}{x}−\mathrm{24}\right\}{e}^{\frac{{x}}{\mathrm{2}}} \left[+\mathrm{3}\left\{\mathrm{2}{x}^{\mathrm{2}} {e}^{\frac{{x}}{\mathrm{2}}} \:−\mathrm{2}\left(\mathrm{2}{xe}^{\frac{{x}}{\mathrm{2}}} −\mathrm{4}{e}^{\frac{{x}}{\mathrm{2}}} \right)\right\}\right. \\ $$$$+\frac{\mathrm{11}}{\mathrm{2}}\left\{\mathrm{2}{xe}^{\frac{{x}}{\mathrm{2}}} −\mathrm{4}{e}^{\frac{{x}}{\mathrm{2}}} \right\}\:+\mathrm{4}\left\{\mathrm{2}{e}^{\frac{{x}}{\mathrm{2}}} \right\}\:+{c} \\ $$$${y}\:={K}\left({x}\right){e}^{−\frac{{x}}{\mathrm{2}}} \:\Rightarrow{y}\left({x}\right)\:=... \\ $$

Commented by mathmax by abdo last updated on 05/Aug/19

2) x^2 y^′ +3xy =x^3 +2x^2 ⇒xy^′ +3y =x^2 +2x (e) (he) ⇒xy^′ +3y =0 ⇒xy^′ =−3y ⇒(y^′ /y) =((−3)/x) ⇒ln∣y∣ =−3ln∣x∣+λ ⇒ y(x) =(k/(∣x∣^3 )) let find the solution on ]0,+∞[ ⇒y(x)=(k/x^3 ) mvc method →y^′ =(k^′ /x^3 ) +k(−3(x^2 /x^6 ))=(k^′ /x^3 )−((3k)/x^4 ) (e) ⇒(k^′ /x^2 )−((3k)/x^3 ) +((3k)/x^3 ) =x^2 +2x ⇒k^′ =x^4 +3x^3 ⇒k(x)=∫(x^4 +3x^3 )dx +c ⇒k(x) =(x^5 /5) +(3/4)x^4 +c ⇒y(x)=(1/x^3 ){(x^5 /5) +(3/4)x^4 +c} =(1/5)x^2 +(3/4)x +(c/x^3 ) .

$$\left.\mathrm{2}\right)\:{x}^{\mathrm{2}} {y}^{'} \:+\mathrm{3}{xy}\:={x}^{\mathrm{3}} \:+\mathrm{2}{x}^{\mathrm{2}} \:\Rightarrow{xy}^{'} \:+\mathrm{3}{y}\:\:={x}^{\mathrm{2}} \:+\mathrm{2}{x}\:\left({e}\right) \\ $$$$\left({he}\right)\:\Rightarrow{xy}^{'} \:+\mathrm{3}{y}\:=\mathrm{0}\:\Rightarrow{xy}^{'} \:=−\mathrm{3}{y}\:\Rightarrow\frac{{y}^{'} }{{y}}\:=\frac{−\mathrm{3}}{{x}}\:\Rightarrow{ln}\mid{y}\mid\:=−\mathrm{3}{ln}\mid{x}\mid+\lambda\:\Rightarrow \\ $$$$\left.{y}\left({x}\right)\:=\frac{{k}}{\mid{x}\mid^{\mathrm{3}} }\:\:\:\:{let}\:{find}\:{the}\:{solution}\:{on}\:\right]\mathrm{0},+\infty\left[\:\Rightarrow{y}\left({x}\right)=\frac{{k}}{{x}^{\mathrm{3}} }\right. \\ $$$${mvc}\:{method}\:\rightarrow{y}^{'} =\frac{{k}^{'} }{{x}^{\mathrm{3}} }\:+{k}\left(−\mathrm{3}\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} }\right)=\frac{{k}^{'} }{{x}^{\mathrm{3}} }−\frac{\mathrm{3}{k}}{{x}^{\mathrm{4}} } \\ $$$$ \\ $$$$\left({e}\right)\:\Rightarrow\frac{{k}^{'} }{{x}^{\mathrm{2}} }−\frac{\mathrm{3}{k}}{{x}^{\mathrm{3}} }\:+\frac{\mathrm{3}{k}}{{x}^{\mathrm{3}} }\:={x}^{\mathrm{2}} \:+\mathrm{2}{x}\:\Rightarrow{k}^{'} \:={x}^{\mathrm{4}} \:+\mathrm{3}{x}^{\mathrm{3}} \:\Rightarrow{k}\left({x}\right)=\int\left({x}^{\mathrm{4}} \:+\mathrm{3}{x}^{\mathrm{3}} \right){dx}\:+{c} \\ $$$$\Rightarrow{k}\left({x}\right)\:=\frac{{x}^{\mathrm{5}} }{\mathrm{5}}\:+\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{4}} \:+{c}\:\Rightarrow{y}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\left\{\frac{{x}^{\mathrm{5}} }{\mathrm{5}}\:+\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{4}} \:+{c}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}{x}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}{x}\:+\frac{{c}}{{x}^{\mathrm{3}} }\:. \\ $$

Commented by mathmax by abdo last updated on 05/Aug/19

xy^′ −y =cos(4x) (he) ⇒xy^′ −y =0 ⇒xy^′ =y ⇒(y^′ /y) =(1/x) ⇒ln∣y∣ =ln∣x∣ +λ ⇒ y =k ∣x∣ let find the solution on ]0,+∞[ ⇒y =kx ⇒y^′ =k^′ x +k (e) ⇒k^′ x^2 +kx−kx =cos(4x) ⇒k^′ x^2 =cos(4x) ⇒ k^′ =((cos(4x))/x^2 ) ⇒k(x) =∫ ((cos(4x))/x^2 )dx +c by parts ∫ ((cos(4x))/x^2 )dx =−(1/x)cos(4x)−∫ ((1/x))4sin(4x)dx =−((cos(4x))/x)−4 ∫ ((sin(4x))/x)dx ⇒k(x) =−((cos(4x))/x)−4∫ ((sin(4x))/x)dx +c ⇒y(x) =−cos(4x) −4x ∫^x ((sin(4t))/t)dt +cx

$${xy}^{'} −{y}\:={cos}\left(\mathrm{4}{x}\right) \\ $$$$\left({he}\right)\:\Rightarrow{xy}^{'} −{y}\:=\mathrm{0}\:\Rightarrow{xy}^{'} \:={y}\:\Rightarrow\frac{{y}^{'} }{{y}}\:=\frac{\mathrm{1}}{{x}}\:\Rightarrow{ln}\mid{y}\mid\:={ln}\mid{x}\mid\:+\lambda\:\Rightarrow \\ $$$$\left.{y}\:={k}\:\mid{x}\mid\:\:\:{let}\:{find}\:{the}\:{solution}\:{on}\:\right]\mathrm{0},+\infty\left[\:\Rightarrow{y}\:={kx}\right. \\ $$$$\Rightarrow{y}^{'} ={k}^{'} {x}\:+{k} \\ $$$$\left({e}\right)\:\Rightarrow{k}^{'} {x}^{\mathrm{2}} \:+{kx}−{kx}\:={cos}\left(\mathrm{4}{x}\right)\:\Rightarrow{k}^{'} {x}^{\mathrm{2}} \:={cos}\left(\mathrm{4}{x}\right)\:\Rightarrow \\ $$$${k}^{'} \:=\frac{{cos}\left(\mathrm{4}{x}\right)}{{x}^{\mathrm{2}} }\:\Rightarrow{k}\left({x}\right)\:=\int\:\:\frac{{cos}\left(\mathrm{4}{x}\right)}{{x}^{\mathrm{2}} }{dx}\:+{c}\:\:{by}\:{parts} \\ $$$$\int\:\:\frac{{cos}\left(\mathrm{4}{x}\right)}{{x}^{\mathrm{2}} }{dx}\:=−\frac{\mathrm{1}}{{x}}{cos}\left(\mathrm{4}{x}\right)−\int\:\left(\frac{\mathrm{1}}{{x}}\right)\mathrm{4}{sin}\left(\mathrm{4}{x}\right){dx} \\ $$$$=−\frac{{cos}\left(\mathrm{4}{x}\right)}{{x}}−\mathrm{4}\:\int\:\frac{{sin}\left(\mathrm{4}{x}\right)}{{x}}{dx}\:\Rightarrow{k}\left({x}\right)\:=−\frac{{cos}\left(\mathrm{4}{x}\right)}{{x}}−\mathrm{4}\int\:\frac{{sin}\left(\mathrm{4}{x}\right)}{{x}}{dx}\:+{c} \\ $$$$\Rightarrow{y}\left({x}\right)\:=−{cos}\left(\mathrm{4}{x}\right)\:−\mathrm{4}{x}\:\int^{{x}} \:\frac{{sin}\left(\mathrm{4}{t}\right)}{{t}}{dt}\:+{cx}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com