
Question Number 6588 by Temp last updated on 04/Jul/16

$$\mathrm{Expansion}\:\mathrm{of}\:\mathrm{Q6582} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} {e}^{−{ix}^{\mathrm{2}} } {dx}=??? \\ $$
Commented by FilupSmith last updated on 07/Jul/16
![I=∫_0 ^( ∞) e^(−ix^2 ) dx I^2 =∫_0 ^( ∞) e^(−ix^2 ) dx∫_0 ^( ∞) e^(−iy^2 ) dy I^2 =∫_0 ^( ∞) ∫_0 ^( ∞) e^(−ix^2 −iy^2 ) dxdy I^2 =∫_0 ^( ∞) ∫_0 ^( ∞) e^(−i(x^2 +y^2 )) dxdy x=rcosθ y=rsinθ 0≤r≤∞ 0≤θ≤π/2 I^2 =∫_0 ^( π/2) ∫_0 ^( ∞) re^(−ir^2 ) drdθ ← unsure if correct jacobian I^2 =∫_0 ^( ∞) re^(−ir^2 ) dr∫_0 ^( π/2) dθ u=r^2 du=2rdr I^2 =(1/2)∫_0 ^( ∞) e^(−iu) du∫_0 ^( π/2) dθ I^2 =(1/2)(−(1/i))[e^(−ir^2 ) ]_0 ^∞ [θ]_0 ^(π/2) I^2 =(1/4)πi[(1/e^(i∞) )−(1/e^(i0) )] I^2 =(1/4)πi[(1/e^(i∞) )−1] ???????](Q6629.png)
$${I}=\int_{\mathrm{0}} ^{\:\infty} {e}^{−{ix}^{\mathrm{2}} } {dx} \\ $$$${I}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\:\infty} {e}^{−{ix}^{\mathrm{2}} } {dx}\int_{\mathrm{0}} ^{\:\infty} {e}^{−{iy}^{\mathrm{2}} } {dy} \\ $$$${I}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} {e}^{−{ix}^{\mathrm{2}} −{iy}^{\mathrm{2}} } {dxdy} \\ $$$${I}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} {e}^{−{i}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)} {dxdy} \\ $$$${x}={r}\mathrm{cos}\theta \\ $$$${y}={r}\mathrm{sin}\theta \\ $$$$\mathrm{0}\leqslant{r}\leqslant\infty \\ $$$$\mathrm{0}\leqslant\theta\leqslant\pi/\mathrm{2} \\ $$$${I}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \int_{\mathrm{0}} ^{\:\infty} {re}^{−{ir}^{\mathrm{2}} } {drd}\theta\:\:\:\leftarrow\:\mathrm{unsure}\:\mathrm{if}\:\mathrm{correct}\:\mathrm{jacobian} \\ $$$${I}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\:\infty} {re}^{−{ir}^{\mathrm{2}} } {dr}\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {d}\theta \\ $$$${u}={r}^{\mathrm{2}} \\ $$$${du}=\mathrm{2}{rdr} \\ $$$${I}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} {e}^{−{iu}} {du}\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {d}\theta \\ $$$${I}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{{i}}\right)\left[{e}^{−{ir}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} \left[\theta\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$${I}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\pi{i}\left[\frac{\mathrm{1}}{{e}^{{i}\infty} }−\frac{\mathrm{1}}{{e}^{{i}\mathrm{0}} }\right] \\ $$$${I}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\pi{i}\left[\frac{\mathrm{1}}{{e}^{{i}\infty} }−\mathrm{1}\right] \\ $$$$??????? \\ $$
Commented by prakash jain last updated on 07/Jul/16
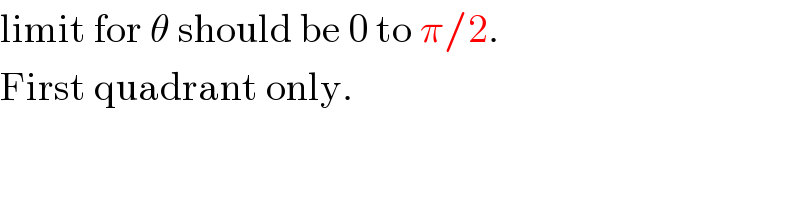
$$\mathrm{limit}\:\mathrm{for}\:\theta\:\mathrm{should}\:\mathrm{be}\:\mathrm{0}\:\mathrm{to}\:\pi/\mathrm{2}. \\ $$$$\mathrm{First}\:\mathrm{quadrant}\:\mathrm{only}. \\ $$
Commented by FilupSmith last updated on 07/Jul/16

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{the}\:\mathrm{correction}!\:\mathrm{I}\:\mathrm{don}'\mathrm{t} \\ $$$$\mathrm{know}\:\mathrm{much}\:\mathrm{about}\:\mathrm{changing}\:\mathrm{into}\:\mathrm{polar} \\ $$$$\mathrm{coordinates} \\ $$
