
Question Number 65924 by mathmax by abdo last updated on 05/Aug/19
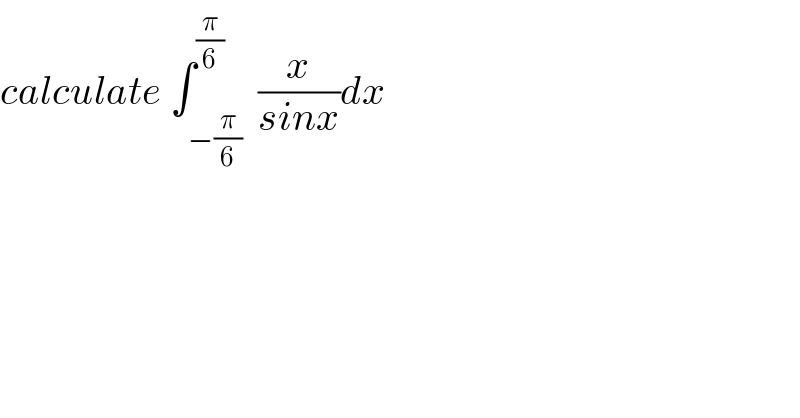
$${calculate}\:\int_{−\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{{x}}{{sinx}}{dx}\: \\ $$
Commented by mathmax by abdo last updated on 07/Aug/19
![let I =∫_(−(π/6)) ^(π/6) (x/(sinx))dx let find approximate value we have I =2∫_0 ^(π/6) (x/(sinx))dx but sinx =Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)!)) with radiusR=+∞ ⇒sinx =x−(x^3 /(3!)) +(x^5 /(5!))−....⇒x−(x^3 /(3!))≤sinx ≤x ⇒(1/x)≤(1/(sinx))≤(1/(x−(x^3 /6))) ⇒1≤(x/(sinx))≤(1/(1−(x^2 /6))) for x∈]0,(π/6)] ⇒∫_0 ^(π/6) 1dx ≤∫_0 ^(π/6) (x/(sinx))dx≤∫_0 ^(π/6) ((6dx)/(6−x^2 )) (π/3)≤ 2∫_0 ^(π/6) (x/(sinx))dx ≤12 ∫_0 ^(π/6) (dx/(6−x^2 )) ⇒(π/3)≤I ≤12∫_0 ^(π/6) (dx/(6−x^2 )) ∫_0 ^(π/6) (dx/(6−x^2 )) =−∫_0 ^(π/6) (dx/((x−(√6))(x+(√6)))) =−(1/(2(√6)))∫_0 ^(π/6) {(1/(x−(√6)))−(1/(x+(√6)))}dx =−(1/(2(√6)))[ln∣((x−(√6))/(x+(√6)))∣]_0 ^(π/6) =−(1/(2(√6)))ln∣(((π/6)−(√6))/((π/6)+(√6)))∣ =−(1/(2(√6)))ln∣((π−6(√6))/(π+6(√6)))∣ =(1/(2(√6)))ln(((π+6(√6))/(6(√6)−π))) ⇒(π/3)≤ I ≤(√6)ln(((6(√6)+π)/(6(√6)−π))) let v_0 =(π/6) +((√6)/2)ln(((6(√6)+π)/(6(√6)−π))) v_0 is a better approximation for I .](Q66007.png)
$${let}\:{I}\:=\int_{−\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{{x}}{{sinx}}{dx}\:\:{let}\:{find}\:{approximate}\:{value}\:{we}\:{have} \\ $$$${I}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{{x}}{{sinx}}{dx}\:\:\:\:\:{but}\:{sinx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:{with}\:{radiusR}=+\infty \\ $$$$\Rightarrow{sinx}\:={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}−....\Rightarrow{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\leqslant{sinx}\:\leqslant{x}\:\Rightarrow\frac{\mathrm{1}}{{x}}\leqslant\frac{\mathrm{1}}{{sinx}}\leqslant\frac{\mathrm{1}}{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}} \\ $$$$\left.\Rightarrow\left.\mathrm{1}\leqslant\frac{{x}}{{sinx}}\leqslant\frac{\mathrm{1}}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}}\:\:\:{for}\:{x}\in\right]\mathrm{0},\frac{\pi}{\mathrm{6}}\right]\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{1}{dx}\:\leqslant\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{{x}}{{sinx}}{dx}\leqslant\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{\mathrm{6}{dx}}{\mathrm{6}−{x}^{\mathrm{2}} } \\ $$$$\frac{\pi}{\mathrm{3}}\leqslant\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\:\frac{{x}}{{sinx}}{dx}\:\leqslant\mathrm{12}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{{dx}}{\mathrm{6}−{x}^{\mathrm{2}} }\:\Rightarrow\frac{\pi}{\mathrm{3}}\leqslant{I}\:\leqslant\mathrm{12}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{{dx}}{\mathrm{6}−{x}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{{dx}}{\mathrm{6}−{x}^{\mathrm{2}} }\:=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\:\frac{{dx}}{\left({x}−\sqrt{\mathrm{6}}\right)\left({x}+\sqrt{\mathrm{6}}\right)}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\:\left\{\frac{\mathrm{1}}{{x}−\sqrt{\mathrm{6}}}−\frac{\mathrm{1}}{{x}+\sqrt{\mathrm{6}}}\right\}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\left[{ln}\mid\frac{{x}−\sqrt{\mathrm{6}}}{{x}+\sqrt{\mathrm{6}}}\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}{ln}\mid\frac{\frac{\pi}{\mathrm{6}}−\sqrt{\mathrm{6}}}{\frac{\pi}{\mathrm{6}}+\sqrt{\mathrm{6}}}\mid \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}{ln}\mid\frac{\pi−\mathrm{6}\sqrt{\mathrm{6}}}{\pi+\mathrm{6}\sqrt{\mathrm{6}}}\mid\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}{ln}\left(\frac{\pi+\mathrm{6}\sqrt{\mathrm{6}}}{\mathrm{6}\sqrt{\mathrm{6}}−\pi}\right)\:\Rightarrow\frac{\pi}{\mathrm{3}}\leqslant\:{I}\:\leqslant\sqrt{\mathrm{6}}{ln}\left(\frac{\mathrm{6}\sqrt{\mathrm{6}}+\pi}{\mathrm{6}\sqrt{\mathrm{6}}−\pi}\right) \\ $$$${let}\:{v}_{\mathrm{0}} =\frac{\pi}{\mathrm{6}}\:+\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}{ln}\left(\frac{\mathrm{6}\sqrt{\mathrm{6}}+\pi}{\mathrm{6}\sqrt{\mathrm{6}}−\pi}\right) \\ $$$${v}_{\mathrm{0}} {is}\:{a}\:{better}\:{approximation}\:{for}\:{I}\:. \\ $$$$ \\ $$
