Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 65950 by ajfour last updated on 06/Aug/19

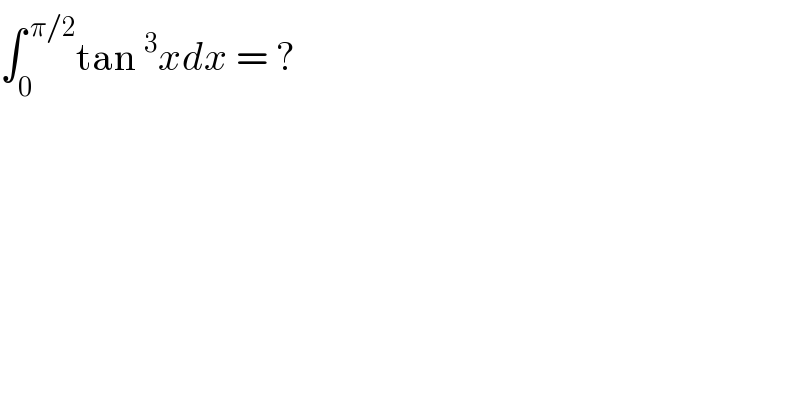
∫_0 ^( π/2) tan^3 xdx = ?

$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{tan}\:^{\mathrm{3}} {xdx}\:=\:? \\ $$

Answered by Tupac Shakur last updated on 06/Aug/19

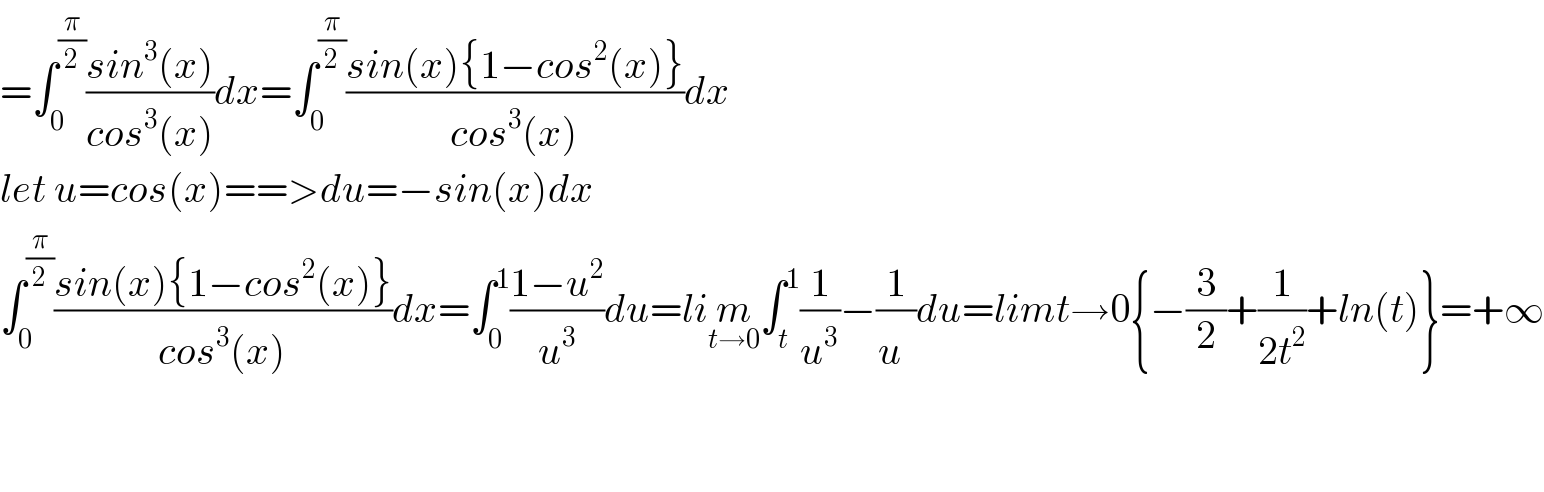
=∫_0 ^(π/2) ((sin^3 (x))/(cos^3 (x)))dx=∫_0 ^(π/2) ((sin(x){1−cos^2 (x)})/(cos^3 (x)))dx let u=cos(x)==>du=−sin(x)dx ∫_0 ^(π/2) ((sin(x){1−cos^2 (x)})/(cos^3 (x)))dx=∫_0 ^1 ((1−u^2 )/u^3 )du=lim_(t→0) ∫_t ^1 (1/u^3 )−(1/u^ )du=limt→0{−(3/2)+(1/(2t^2 ))+ln(t)}=+∞

$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{3}} \left({x}\right)}{{cos}^{\mathrm{3}} \left({x}\right)}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}\left({x}\right)\left\{\mathrm{1}−{cos}^{\mathrm{2}} \left({x}\right)\right\}}{{cos}^{\mathrm{3}} \left({x}\right)}{dx} \\ $$$${let}\:{u}={cos}\left({x}\right)==>{du}=−{sin}\left({x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}\left({x}\right)\left\{\mathrm{1}−{cos}^{\mathrm{2}} \left({x}\right)\right\}}{{cos}^{\mathrm{3}} \left({x}\right)}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{u}^{\mathrm{2}} }{{u}^{\mathrm{3}} }{du}={li}\underset{{t}\rightarrow\mathrm{0}} {{m}}\int_{{t}} ^{\mathrm{1}} \frac{\mathrm{1}}{{u}^{\mathrm{3}} }−\frac{\mathrm{1}}{{u}^{} }{du}={limt}\rightarrow\mathrm{0}\left\{−\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }+{ln}\left({t}\right)\right\}=+\infty \\ $$$$ \\ $$$$ \\ $$

Answered by Tanmay chaudhury last updated on 06/Aug/19

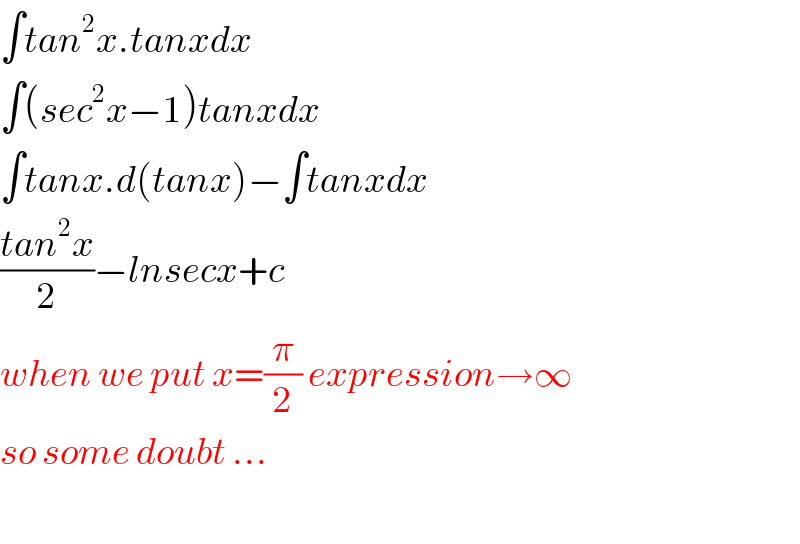
∫tan^2 x.tanxdx ∫(sec^2 x−1)tanxdx ∫tanx.d(tanx)−∫tanxdx ((tan^2 x)/2)−lnsecx+c when we put x=(π/2) expression→∞ so some doubt ...

$$\int{tan}^{\mathrm{2}} {x}.{tanxdx} \\ $$$$\int\left({sec}^{\mathrm{2}} {x}−\mathrm{1}\right){tanxdx} \\ $$$$\int{tanx}.{d}\left({tanx}\right)−\int{tanxdx} \\ $$$$\frac{{tan}^{\mathrm{2}} {x}}{\mathrm{2}}−{lnsecx}+{c} \\ $$$${when}\:{we}\:{put}\:{x}=\frac{\pi}{\mathrm{2}}\:{expression}\rightarrow\infty \\ $$$${so}\:{some}\:{doubt}\:... \\ $$$$ \\ $$

Answered by ajfour last updated on 06/Aug/19

∫_0 ^( π/2) ((tan^3 xsec^2 xdx)/((1+tan^2 x))) let tan x=t ∫_0 ^( ∞) ((t^3 dt)/(1+t^2 )) = ∫_0 ^∞ ((t(t^2 +1−1)dt)/(1+t^2 )) =∫_0 ^( c→∞) [(tdt)−(1/2)(((2tdt)/(1+t^2 )))] = lim_(b→∞) [(b/2)−(1/2)ln (1+b)] f(b)=lim_(b→∞) ((ln (1+b))/b)=lim_(b→∞) (1/(1+b)) →0 ⇒ Integral →∞ (but answer in book R.S. Agarwal for class XII is a finite one !)

$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\frac{\mathrm{tan}\:^{\mathrm{3}} {x}\mathrm{sec}\:^{\mathrm{2}} {xdx}}{\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}\right)} \\ $$$${let}\:\:\mathrm{tan}\:{x}={t} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{\mathrm{3}} {dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\infty} \:\frac{{t}\left({t}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}\right){dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\:{c}\rightarrow\infty} \left[\left({tdt}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}{tdt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)\right] \\ $$$$\:=\:\underset{{b}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{b}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+{b}\right)\right] \\ $$$${f}\left({b}\right)=\underset{{b}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{ln}\:\left(\mathrm{1}+{b}\right)}{{b}}=\underset{{b}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{1}+{b}}\:\rightarrow\mathrm{0} \\ $$$$\Rightarrow\:{Integral}\:\rightarrow\infty \\ $$$$\left({but}\:{answer}\:{in}\:{book}\:{R}.{S}.\:{Agarwal}\right. \\ $$$$\left.{for}\:{class}\:{XII}\:{is}\:{a}\:{finite}\:{one}\:!\right) \\ $$$$ \\ $$

Commented by MJS last updated on 06/Aug/19

post his answer please...

$$\mathrm{post}\:\mathrm{his}\:\mathrm{answer}\:\mathrm{please}... \\ $$

Answered by MJS last updated on 06/Aug/19

∫tan^n x dx=(1/(n−1))tan^(n−1) x −∫tan^(n−2) x dx ∫tan^3 x dx=(1/2)tan^2 x −∫tan x dx= =(1/2)tan^2 x +ln cos x +C ∫_0 ^(π/2) tan^n x dx=+∞ for n∈N^★ what′s obvious because tan^n x ≥1 for (π/4)≤x<(π/2) and n∈N^★

$$\int\mathrm{tan}^{{n}} \:{x}\:{dx}=\frac{\mathrm{1}}{{n}−\mathrm{1}}\mathrm{tan}^{{n}−\mathrm{1}} \:{x}\:−\int\mathrm{tan}^{{n}−\mathrm{2}} \:{x}\:{dx} \\ $$$$\int\mathrm{tan}^{\mathrm{3}} \:{x}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{\mathrm{2}} \:{x}\:−\int\mathrm{tan}\:{x}\:{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{\mathrm{2}} \:{x}\:+\mathrm{ln}\:\mathrm{cos}\:{x}\:+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mathrm{tan}^{{n}} \:{x}\:{dx}=+\infty\:\mathrm{for}\:{n}\in\mathbb{N}^{\bigstar} \\ $$$$\mathrm{what}'\mathrm{s}\:\mathrm{obvious}\:\mathrm{because}\:\mathrm{tan}^{{n}} \:{x}\:\geqslant\mathrm{1}\:\mathrm{for}\:\frac{\pi}{\mathrm{4}}\leqslant{x}<\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{and}\:{n}\in\mathbb{N}^{\bigstar} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com