Question Number 65980 by Tony Lin last updated on 07/Aug/19
Commented by Tanmay chaudhury last updated on 07/Aug/19
Answered by Tanmay chaudhury last updated on 07/Aug/19
![eqn of circle centre A is x^2 +y^2 =10^2 eqn of circle centre mid point of AD x^2 +(y−5)^2 =5^2 eqn of circle centre mid point of CD (x−5)^2 +(y−5)^2 =5^2 point P... (x−5)^2 +(y−5)^2 =5^2 x^2 +(y−5)^2 =5^2 substruct −10x+25=0 x_P =(5/2) (y−5)^2 =25−((25)/4)=((75)/4) y=5±((5(√3))/2)→y=((5(1+(√3) ))/2) negetive value of y not feasible P((5/2),((5(1+(√3) ))/2)) for point Q solve x^2 +y^2 =10^2 (x−5)^2 +(y−5)^2 =5^2 100−10x−10y+50=25 x+y=((125)/(10))=((25)/2) x^2 +((625)/4)−25x+x^2 =100 8x^2 −100x+625−400=0 8x^2 −100x+225=0 x_Q =((100±(√(10000−32×225)))/(16)) x_Q =((100±20(√7))/(16))→x_Q =((25+5(√7))/4) [−ve ignored] y=((25)/2)−((25+5(√7))/4)=((25−5(√7))/4) so reqiuired area ∫_0 ^x_Q (√(100−x^2 )) dx−((π((5/2))^2 )/4)−∫_x_P ^x_Q 5+(√(25−(x−5)^2 )) dx it is reflection of thought...](Q65982.png)
$${eqn}\:{of}\:{circle}\:{centre}\:{A}\:{is}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} \\ $$$${eqn}\:{of}\:{circle}\:{centre}\:{mid}\:{point}\:{of}\:{AD}\:{x}^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$${eqn}\:{of}\:{circle}\:{centre}\:{mid}\:{point}\:{of}\:{CD}\:\left({x}−\mathrm{5}\right)^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$${point}\:{P}... \\ $$$$\left({x}−\mathrm{5}\right)^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$${substruct} \\ $$$$−\mathrm{10}{x}+\mathrm{25}=\mathrm{0}\:\:{x}_{{P}} =\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{25}−\frac{\mathrm{25}}{\mathrm{4}}=\frac{\mathrm{75}}{\mathrm{4}}\:\:{y}=\mathrm{5}\pm\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}}\rightarrow{y}=\frac{\mathrm{5}\left(\mathrm{1}+\sqrt{\mathrm{3}}\:\right)}{\mathrm{2}} \\ $$$${negetive}\:{value}\:{of}\:{y}\:{not}\:{feasible} \\ $$$${P}\left(\frac{\mathrm{5}}{\mathrm{2}},\frac{\mathrm{5}\left(\mathrm{1}+\sqrt{\mathrm{3}}\:\right)}{\mathrm{2}}\right) \\ $$$${for}\:{point}\:{Q}\:\:{solve} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} \:\:\:\left({x}−\mathrm{5}\right)^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$$\mathrm{100}−\mathrm{10}{x}−\mathrm{10}{y}+\mathrm{50}=\mathrm{25} \\ $$$${x}+{y}=\frac{\mathrm{125}}{\mathrm{10}}=\frac{\mathrm{25}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{625}}{\mathrm{4}}−\mathrm{25}{x}+{x}^{\mathrm{2}} =\mathrm{100} \\ $$$$\mathrm{8}{x}^{\mathrm{2}} −\mathrm{100}{x}+\mathrm{625}−\mathrm{400}=\mathrm{0} \\ $$$$\mathrm{8}{x}^{\mathrm{2}} −\mathrm{100}{x}+\mathrm{225}=\mathrm{0} \\ $$$${x}_{{Q}} =\frac{\mathrm{100}\pm\sqrt{\mathrm{10000}−\mathrm{32}×\mathrm{225}}}{\mathrm{16}} \\ $$$${x}_{{Q}} =\frac{\mathrm{100}\pm\mathrm{20}\sqrt{\mathrm{7}}}{\mathrm{16}}\rightarrow{x}_{{Q}} =\frac{\mathrm{25}+\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{4}}\:\left[−{ve}\:{ignored}\right] \\ $$$${y}=\frac{\mathrm{25}}{\mathrm{2}}−\frac{\mathrm{25}+\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{4}}=\frac{\mathrm{25}−\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{4}} \\ $$$${so}\:{reqiuired}\:{area} \\ $$$$\int_{\mathrm{0}} ^{{x}_{{Q}} } \sqrt{\mathrm{100}−{x}^{\mathrm{2}} }\:{dx}−\frac{\pi\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{4}}−\int_{{x}_{{P}} } ^{{x}_{{Q}} } \mathrm{5}+\sqrt{\mathrm{25}−\left({x}−\mathrm{5}\right)^{\mathrm{2}} }\:\:{dx} \\ $$$${it}\:{is}\:{reflection}\:{of}\:{thought}... \\ $$
Commented by Kunal12588 last updated on 07/Aug/19
$${i}\:{think}\:{you}\:{got}\:{a}\:{little}\:{wrong}\:{their} \\ $$$${eqn}\:{of}\:{circle}\:{centre}\:{mid}\:{point}\:{of}\:{CD}\:\left({x}−\mathrm{5}\right)^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$${should}\:{be}\:{eqn}\:{of}\:{circle}\:{centre}\:{mid}\:{point}\:{of}\:{CD}\:\left({x}−\mathrm{5}\right)^{\mathrm{2}} +\left({y}−\mathrm{10}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$${by}\:{solving}\:{P}\left(\mathrm{5},\mathrm{5}\right)\:{and}\:{Q}\left(\mathrm{8},\mathrm{6}\right) \\ $$$$\int_{\mathrm{0}} ^{{x}_{{Q}} } \sqrt{\mathrm{100}−{x}^{\mathrm{2}} }\:{dx}−\frac{\pi\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{4}}−\int_{{x}_{{P}} } ^{{x}_{{Q}} } \mathrm{5}+\sqrt{\mathrm{25}−\left({x}−\mathrm{5}\right)^{\mathrm{2}} }\:\:{dx} \\ $$$${also}\:{i}\:{don}'{t}\:{get}\:{subtracting}\:{blue}\:{term} \\ $$$${should}\:{be}\:\int_{\mathrm{0}} ^{{x}_{{Q}} } \sqrt{\mathrm{100}−{x}^{\mathrm{2}} }\:{dx}−\int_{\mathrm{0}} ^{{x}_{{P}} } \mathrm{5}+\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }{dx}−\int_{{x}_{{P}} } ^{{x}_{{Q}} } \mathrm{10}+\sqrt{\mathrm{25}−\left({x}−\mathrm{5}\right)^{\mathrm{2}} }\:\:{dx} \\ $$
Commented by Tony Lin last updated on 08/Aug/19
$${thanks}\:{sir} \\ $$
Answered by MJS last updated on 07/Aug/19
$${A}=\begin{pmatrix}{−\mathrm{5}}\\{−\mathrm{5}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\mathrm{5}}\\{−\mathrm{5}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{\mathrm{5}}\\{\mathrm{5}}\end{pmatrix} \\ $$$${D}=\begin{pmatrix}{−\mathrm{5}}\\{\mathrm{5}}\end{pmatrix}\:\:{P}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:{Q}=\begin{pmatrix}{\mathrm{3}}\\{\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{red}\:\mathrm{area} \\ $$$$\underset{−\mathrm{5}} {\overset{\mathrm{3}} {\int}}\left(−\mathrm{5}+\sqrt{\mathrm{100}−\left({x}+\mathrm{5}\right)^{\mathrm{2}} }\right){dx}−\underset{−\mathrm{5}} {\overset{\mathrm{0}} {\int}}\sqrt{\mathrm{25}−\left({x}+\mathrm{5}\right)^{\mathrm{2}} }{dx}−\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\left(\mathrm{5}−\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }\right){dx}= \\ $$$$=\frac{\mathrm{25}}{\mathrm{4}}\left(\mathrm{8arcsin}\:\frac{\mathrm{4}}{\mathrm{5}}\:+\mathrm{2arcsin}\:\frac{\mathrm{3}}{\mathrm{5}}\:−\pi−\mathrm{4}\right)= \\ $$$$=\frac{\mathrm{25}}{\mathrm{2}}\left(\pi−\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\frac{\mathrm{10296}}{\mathrm{11753}}\right)\approx\mathrm{9}.\mathrm{77357} \\ $$$$\approx\mathrm{9}.\mathrm{77357} \\ $$
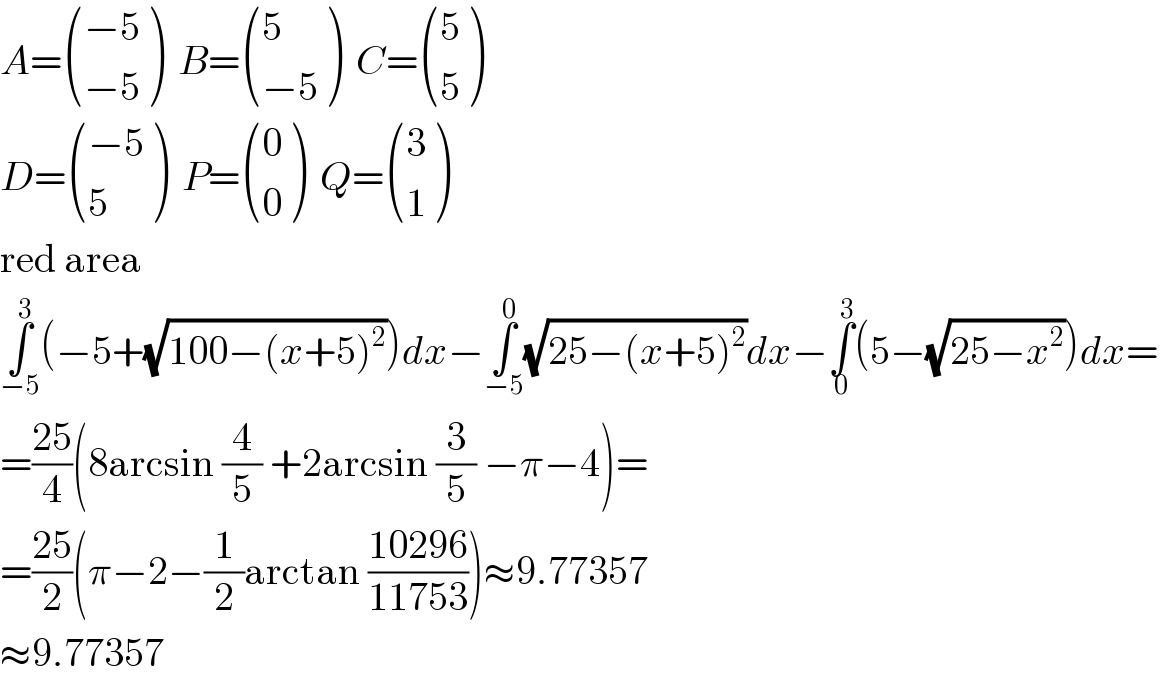
Commented by Tony Lin last updated on 08/Aug/19
$${thanks}\:{sir} \\ $$
Answered by mr W last updated on 07/Aug/19
Commented by mr W last updated on 07/Aug/19
$$\varphi+\theta=\pi \\ $$$$\mathrm{10}\:\mathrm{sin}\:\frac{\varphi}{\mathrm{2}}=\mathrm{5}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{2}\:\mathrm{sin}\:\frac{\varphi}{\mathrm{2}}=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\varphi}{\mathrm{2}}\right)=\mathrm{cos}\:\frac{\varphi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\varphi}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\varphi=\frac{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\Rightarrow\varphi=\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\pi−\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$${A}_{{green}} =\mathrm{2}×\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{1}\right)=\frac{\mathrm{25}\pi}{\mathrm{2}}−\mathrm{25} \\ $$$${A}_{{green}} +{A}_{{red}} =\frac{\mathrm{10}^{\mathrm{2}} }{\mathrm{2}}\left(\varphi−\mathrm{sin}\:\varphi\right)+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−\mathrm{sin}\:\theta\right) \\ $$$$=\mathrm{50}\left(\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{5}}\right)+\frac{\mathrm{25}}{\mathrm{2}}\left(\pi−\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$$=\mathrm{75}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\mathrm{50}+\frac{\mathrm{25}\pi}{\mathrm{2}} \\ $$$$\Rightarrow{A}_{{red}} =\mathrm{75}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\mathrm{50}+\frac{\mathrm{25}\pi}{\mathrm{2}}−\frac{\mathrm{25}\pi}{\mathrm{2}}+\mathrm{25} \\ $$$$\Rightarrow{A}_{{red}} =\mathrm{25}\left(\mathrm{3}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)=\mathrm{9}.\mathrm{7736} \\ $$
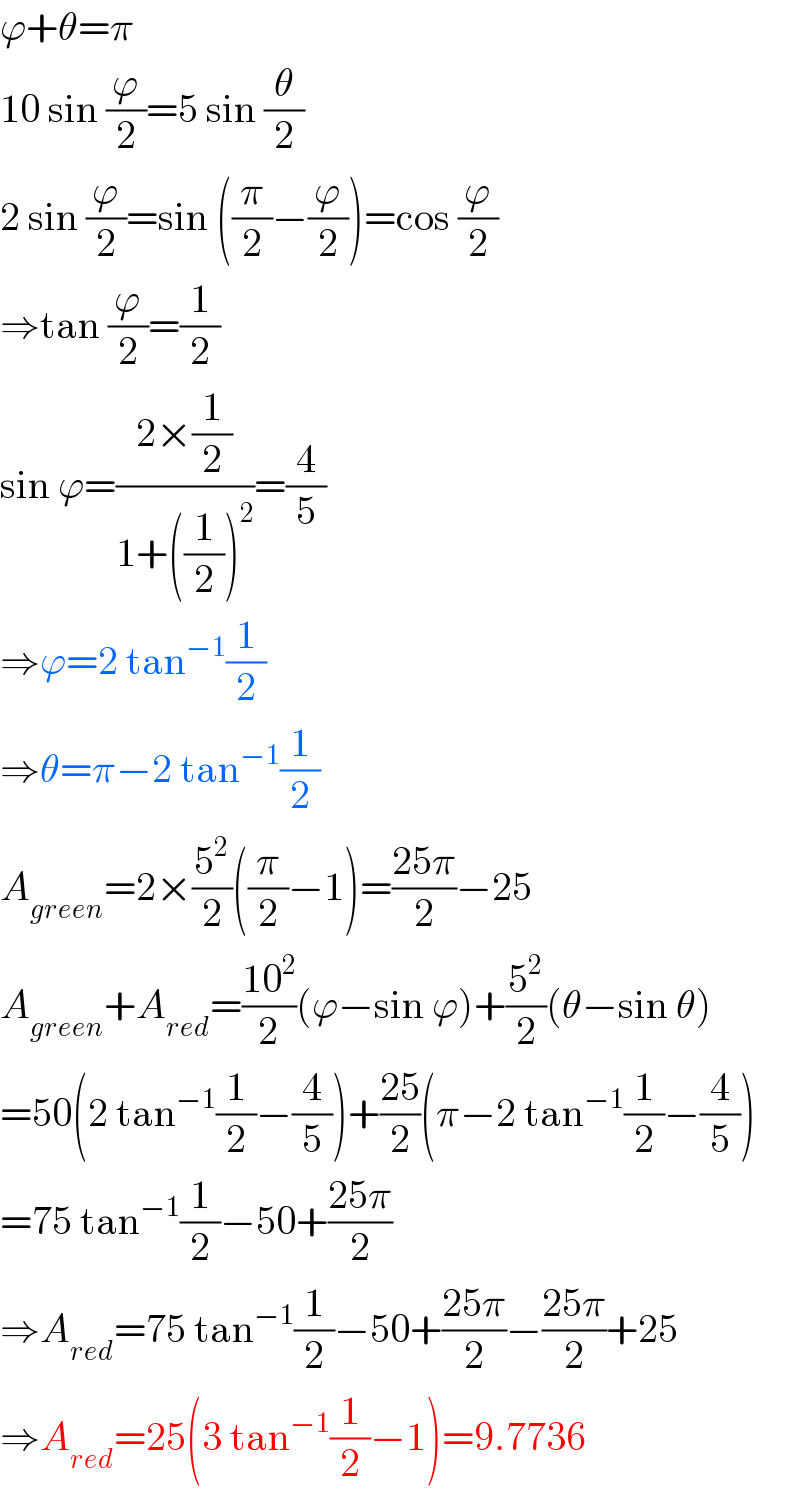
Commented by mr W last updated on 07/Aug/19
Commented by Tony Lin last updated on 08/Aug/19
$${thanks}\:{sir} \\ $$