Previous in Relation and Functions Next in Relation and Functions
Question Number 66172 by mathmax by abdo last updated on 10/Aug/19
$$ \\ $$$${let}\:{A}_{{n}} =\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\:\:\:{calculate}\:{lim}_{{n}\rightarrow+\infty} \:\frac{{ln}\left({A}_{{n}} \right)}{{n}} \\ $$
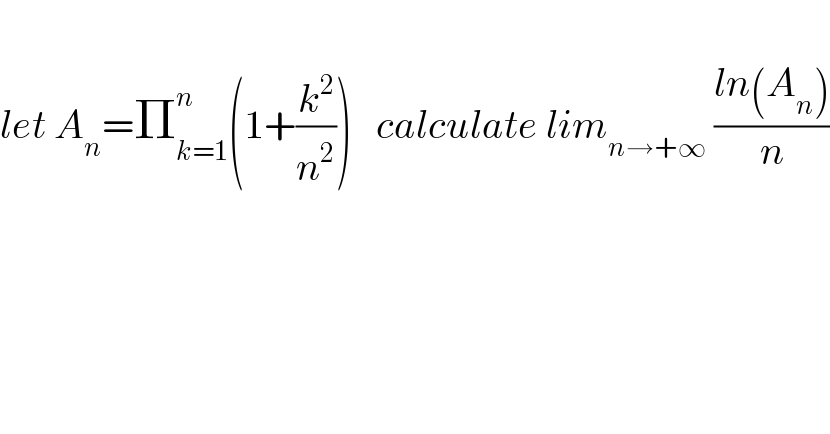
Commented by Prithwish sen last updated on 11/Aug/19
![lim_(n→∞) (1/n) Σ_(k=1) ^n ln[1+((k/n))^2 ] = ∫_0 ^1 ln(1+x^2 )dx =[xln(1+x^2 )−2x+2tan^(−1) x]_0 ^1 =ln2 −2+(π/2) please check.](Q66174.png)
$$\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \frac{\mathrm{1}}{\mathrm{n}}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left[\mathrm{1}+\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} \right]\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$=\left[\mathrm{xln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2x}+\mathrm{2tan}^{−\mathrm{1}} \mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{ln2}\:−\mathrm{2}+\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
Commented by mathmax by abdo last updated on 10/Aug/19
![we have ln(A_n )=Σ_(k=1) ^n ln(1+(k^2 /n^2 )) ⇒((ln(A_n ))/n) =(1/n)Σ_(k=1) ^n ln(1+((k/n))^2 ) we get a Rieman sum ⇒lim_(n→+∞) ((ln(A_n ))/n) =∫_0 ^1 ln(1+x^2 )dx by parts ∫_0 ^1 ln(1+x^2 )dx =[xln(1+x^2 )]_0 ^1 −∫_0 ^1 x((2x)/(1+x^2 ))dx =ln(2)−2 ∫_0 ^1 ((x^2 +1−1)/(x^2 +1))dx =ln(2)−2 +2 ∫_0 ^1 (dx/(1+x^2 )) =ln(2)−2 +2[arctanx]_0 ^1 =ln(2)−2+2×(π/4) =ln(2)−2+(π/2) finally lim_(n→+∞) ((ln(A_n ))/n) =(π/2) +ln(2)−2 .](Q66187.png)
$${we}\:{have}\:{ln}\left({A}_{{n}} \right)=\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\:\Rightarrow\frac{{ln}\left({A}_{{n}} \right)}{{n}}\:=\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} \right) \\ $$$${we}\:{get}\:{a}\:{Rieman}\:{sum}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \frac{{ln}\left({A}_{{n}} \right)}{{n}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$${by}\:{parts}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:=\left[{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} {x}\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={ln}\left(\mathrm{2}\right)−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{2}\left[{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} ={ln}\left(\mathrm{2}\right)−\mathrm{2}+\mathrm{2}×\frac{\pi}{\mathrm{4}}\:={ln}\left(\mathrm{2}\right)−\mathrm{2}+\frac{\pi}{\mathrm{2}} \\ $$$${finally}\:{lim}_{{n}\rightarrow+\infty} \:\frac{{ln}\left({A}_{{n}} \right)}{{n}}\:=\frac{\pi}{\mathrm{2}}\:+{ln}\left(\mathrm{2}\right)−\mathrm{2}\:. \\ $$
Commented by Prithwish sen last updated on 10/Aug/19
$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
Commented by mathmax by abdo last updated on 10/Aug/19
$${you}\:{are}\:{welcome}\:{sir}. \\ $$