Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 66213 by mathmax by abdo last updated on 10/Aug/19

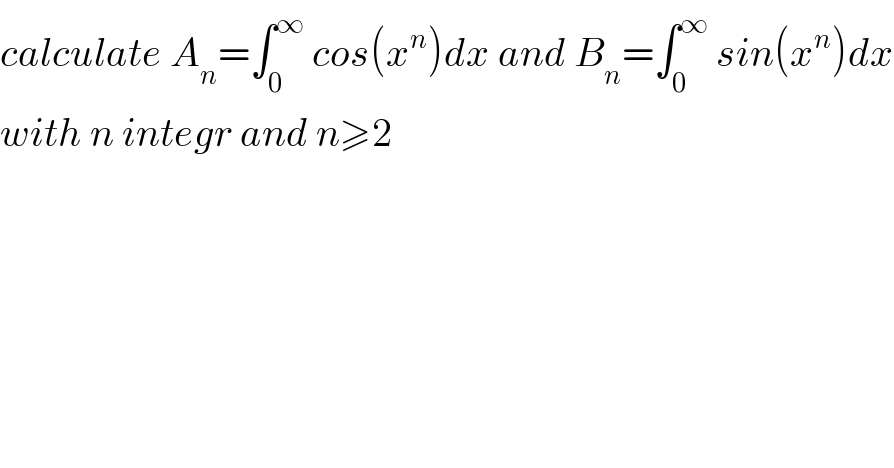
calculate A_n =∫_0 ^∞ cos(x^n )dx and B_n =∫_0 ^∞ sin(x^n )dx with n integr and n≥2

$${calculate}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{cos}\left({x}^{{n}} \right){dx}\:{and}\:{B}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{sin}\left({x}^{{n}} \right){dx} \\ $$$${with}\:{n}\:{integr}\:{and}\:{n}\geqslant\mathrm{2} \\ $$

Commented by ~ À ® @ 237 ~ last updated on 11/Aug/19

When using your method , Let state z_n = a_n +ib_n , then z_n =∫_0 ^∞ e^(ix^n ) dx let change u=(x^n /i) , x=(iu)^(1/n) ⇒ dx= (i/n)(iu)^((1/n) −1) du But i don′t understand why the domain is still R_(+ ) it ought to be iR_+ z_n = (((i)^(1/n) )/n) ∫_0 ^∞ u^((1/n) −1) e^(−u) du=(i^(1/n) /n) Γ((1/n))=(e^((iπ)/(2n)) /n) Γ((1/n)) So a_n =Re(z_n )=(1/n)cos((π/(2n)))Γ((1/n)) and b_n = (1/n)sin((π/(2n)))Γ((1/n))

$$ \\ $$$$ \\ $$$${When}\:{using}\:{your}\:{method}\:, \\ $$$${Let}\:\:{state}\:\:{z}_{{n}} =\:{a}_{{n}} +{ib}_{{n}} \:\:,\:{then}\:{z}_{{n}} =\int_{\mathrm{0}} ^{\infty} {e}^{{ix}^{{n}} } {dx} \\ $$$${let}\:{change}\:{u}=\frac{{x}^{{n}} }{{i}}\:\:\:,\:{x}=\left({iu}\right)^{\frac{\mathrm{1}}{{n}}} \:\Rightarrow\:{dx}=\:\frac{{i}}{{n}}\left({iu}\right)^{\frac{\mathrm{1}}{{n}}\:−\mathrm{1}} {du} \\ $$$${But}\:{i}\:{don}'{t}\:{understand}\:{why}\:{the}\:{domain}\:{is}\:{still}\:\mathbb{R}_{+\:\:} {it}\:{ought}\:{to}\:{be}\:\:\:{i}\mathbb{R}_{+} \\ $$$${z}_{{n}} =\:\frac{\left({i}\right)^{\frac{\mathrm{1}}{{n}}} }{{n}}\:\int_{\mathrm{0}} ^{\infty} \:{u}^{\frac{\mathrm{1}}{{n}}\:−\mathrm{1}} {e}^{−{u}} \:{du}=\frac{{i}^{\frac{\mathrm{1}}{{n}}} }{{n}}\:\Gamma\left(\frac{\mathrm{1}}{{n}}\right)=\frac{{e}^{\frac{{i}\pi}{\mathrm{2}{n}}} }{{n}}\:\Gamma\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$${So}\:{a}_{{n}} ={Re}\left({z}_{{n}} \right)=\frac{\mathrm{1}}{{n}}{cos}\left(\frac{\pi}{\mathrm{2}{n}}\right)\Gamma\left(\frac{\mathrm{1}}{{n}}\right)\:\:{and}\:{b}_{{n}} =\:\frac{\mathrm{1}}{{n}}{sin}\left(\frac{\pi}{\mathrm{2}{n}}\right)\Gamma\left(\frac{\mathrm{1}}{{n}}\right)\:\:\:\:\: \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 11/Aug/19

thank you sir.

$${thank}\:{you}\:{sir}. \\ $$

Commented by mathmax by abdo last updated on 11/Aug/19

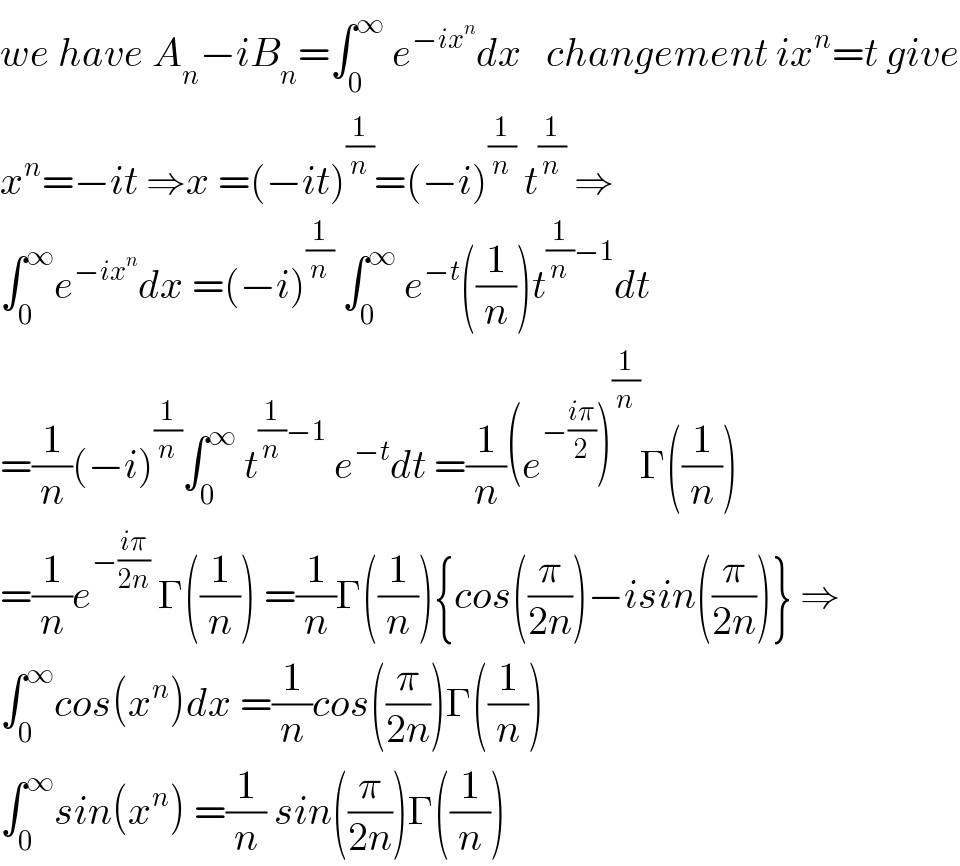
we have A_n −iB_n =∫_0 ^∞ e^(−ix^n ) dx changement ix^n =t give x^n =−it ⇒x =(−it)^(1/n) =(−i)^(1/n) t^(1/n) ⇒ ∫_0 ^∞ e^(−ix^n ) dx =(−i)^(1/n) ∫_0 ^∞ e^(−t) ((1/n))t^((1/n)−1) dt =(1/n)(−i)^(1/n) ∫_0 ^∞ t^((1/n)−1) e^(−t) dt =(1/n)(e^(−((iπ)/2)) )^(1/n) Γ((1/n)) =(1/n)e^(−((iπ)/(2n))) Γ((1/n)) =(1/n)Γ((1/n)){cos((π/(2n)))−isin((π/(2n)))} ⇒ ∫_0 ^∞ cos(x^n )dx =(1/n)cos((π/(2n)))Γ((1/n)) ∫_0 ^∞ sin(x^n ) =(1/n) sin((π/(2n)))Γ((1/n))

$${we}\:{have}\:{A}_{{n}} −{iB}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ix}^{{n}} } {dx}\:\:\:{changement}\:{ix}^{{n}} ={t}\:{give} \\ $$$${x}^{{n}} =−{it}\:\Rightarrow{x}\:=\left(−{it}\right)^{\frac{\mathrm{1}}{{n}}} =\left(−{i}\right)^{\frac{\mathrm{1}}{{n}}} \:{t}^{\frac{\mathrm{1}}{{n}}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{ix}^{{n}} } {dx}\:=\left(−{i}\right)^{\frac{\mathrm{1}}{{n}}} \:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} \left(\frac{\mathrm{1}}{{n}}\right){t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{{n}}\left(−{i}\right)^{\frac{\mathrm{1}}{{n}}} \int_{\mathrm{0}} ^{\infty} \:{t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \:{e}^{−{t}} {dt}\:=\frac{\mathrm{1}}{{n}}\left({e}^{−\frac{{i}\pi}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{{n}}} \Gamma\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$$=\frac{\mathrm{1}}{{n}}{e}^{−\frac{{i}\pi}{\mathrm{2}{n}}} \:\Gamma\left(\frac{\mathrm{1}}{{n}}\right)\:=\frac{\mathrm{1}}{{n}}\Gamma\left(\frac{\mathrm{1}}{{n}}\right)\left\{{cos}\left(\frac{\pi}{\mathrm{2}{n}}\right)−{isin}\left(\frac{\pi}{\mathrm{2}{n}}\right)\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} {cos}\left({x}^{{n}} \right){dx}\:=\frac{\mathrm{1}}{{n}}{cos}\left(\frac{\pi}{\mathrm{2}{n}}\right)\Gamma\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} {sin}\left({x}^{{n}} \right)\:=\frac{\mathrm{1}}{{n}}\:{sin}\left(\frac{\pi}{\mathrm{2}{n}}\right)\Gamma\left(\frac{\mathrm{1}}{{n}}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com